Semelhança de Triângulos Desvendada: para o Ensino Fundamental

Você já observou como as sombras mudam de tamanho ao longo do dia, mas mantêm a mesma forma? Ou como uma foto pode ser ampliada sem perder suas proporções? Esses fenômenos cotidianos estão diretamente relacionados a um conceito matemático fascinante: a Semelhança de Triângulos.

Neste artigo, vamos explorar todos os aspectos desse tema fundamental da geometria, com explicações simples, exemplos práticos e imagens ilustrativas para facilitar seu entendimento. Prepare-se para descobrir como a semelhança de triângulos está presente em nosso dia a dia e como ela pode ser aplicada para resolver problemas reais!

O que é Semelhança de Triângulos

Dois triângulos são considerados semelhantes quando possuem a mesma forma, mas não necessariamente o mesmo tamanho. Em termos matemáticos mais precisos, dois triângulos são semelhantes quando:

1. Seus ângulos correspondentes são congruentes (têm a mesma medida)

2. Seus lados correspondentes são proporcionais

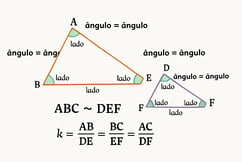
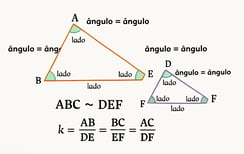
Quando dois triângulos são semelhantes, utilizamos o símbolo "~" para indicar essa relação. Por exemplo, se os triângulos ABC e DEF são semelhantes, escrevemos: ABC ~ DEF.

A semelhança de triângulos é um conceito poderoso que nos permite calcular medidas desconhecidas usando proporções. Se conhecemos as medidas de um triângulo e sabemos que ele é semelhante a outro triângulo do qual conhecemos apenas algumas medidas, podemos determinar as medidas desconhecidas através de relações proporcionais.

Por exemplo, se os triângulos ABC e DEF são semelhantes, e sabemos que a razão de semelhança (a razão entre os lados correspondentes) é 2:1, então cada lado do triângulo DEF será o dobro do lado correspondente no triângulo ABC.

Critérios de Semelhança de Triângulos

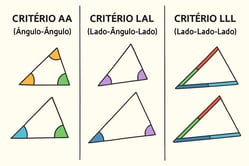
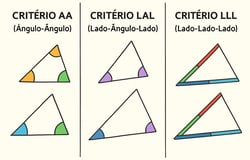
Para determinar se dois triângulos são semelhantes, não precisamos verificar todos os ângulos e lados. Existem três critérios principais que nos permitem estabelecer a semelhança entre triângulos de forma mais eficiente:

Critério AA (Ângulo-Ângulo)

O critério AA estabelece que dois triângulos são semelhantes se dois ângulos de um triângulo são congruentes (iguais) a dois ângulos do outro triângulo.

Como a soma dos ângulos internos de qualquer triângulo é 180°, se dois ângulos de um triângulo são iguais aos dois ângulos correspondentes de outro triângulo, então o terceiro ângulo também será igual. Portanto, na prática, basta verificar a igualdade de dois pares de ângulos correspondentes.

Exemplo: Se no triângulo ABC temos ∠A = 30° e ∠B = 45°, e no triângulo DEF temos ∠D = 30° e ∠E = 45°, então os triângulos ABC e DEF são semelhantes.

Critério LAL (Lado-Ângulo-Lado)

O critério LAL estabelece que dois triângulos são semelhantes se dois lados de um triângulo são proporcionais aos dois lados correspondentes do outro triângulo, e os ângulos incluídos entre esses lados são congruentes.

Exemplo: Se no triângulo ABC temos AB = 6 cm, BC = 8 cm e ∠B = 60°, e no triângulo DEF temos DE = 3 cm, EF = 4 cm e ∠E = 60°, então os triângulos ABC e DEF são semelhantes, pois AB/DE = BC/EF = 2 e os ângulos incluídos são iguais.

Critério LLL (Lado-Lado-Lado)

O critério LLL estabelece que dois triângulos são semelhantes se os três lados de um triângulo são proporcionais aos três lados correspondentes do outro triângulo.

Exemplo: Se no triângulo ABC temos AB = 9 cm, BC = 12 cm e AC = 15 cm, e no triângulo DEF temos DE = 3 cm, EF = 4 cm e DF = 5 cm, então os triângulos ABC e DEF são semelhantes, pois AB/DE = BC/EF = AC/DF = 3.

Estes critérios são ferramentas poderosas que nos permitem identificar triângulos semelhantes sem precisar verificar todas as propriedades, simplificando significativamente a resolução de problemas geométricos.

Propriedades dos Triângulos Semelhantes

Quando dois triângulos são semelhantes, várias propriedades importantes podem ser observadas:

Proporcionalidade dos Lados

Se dois triângulos são semelhantes com razão de semelhança k, então todos os lados correspondentes estão na mesma proporção k. Por exemplo, se ABC ~ DEF com razão k, então:

AB/DE = BC/EF = AC/DF = k

Igualdade dos Ângulos

Os ângulos correspondentes em triângulos semelhantes são sempre iguais:

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Proporcionalidade dos Perímetros

Os perímetros de triângulos semelhantes são proporcionais à razão de semelhança:

Perímetro de ABC / Perímetro de DEF = k

Proporcionalidade das Áreas

As áreas de triângulos semelhantes são proporcionais ao quadrado da razão de semelhança:

Área de ABC / Área de DEF = k²

Esta é uma propriedade muito importante: se um triângulo tem lados duas vezes maiores que outro triângulo semelhante, sua área será quatro vezes maior!

Proporcionalidade de Outros Elementos

Outros elementos correspondentes dos triângulos semelhantes também mantêm relações de proporcionalidade:

• As alturas são proporcionais à razão de semelhança: h₁/h₂ = k

• As medianas são proporcionais à razão de semelhança: m₁/m₂ = k

• As bissetrizes são proporcionais à razão de semelhança: b₁/b₂ = k

Estas propriedades nos permitem calcular diversos elementos de um triângulo quando conhecemos o triângulo semelhante e a razão de semelhança.

Teorema Fundamental da Semelhança

O Teorema Fundamental da Semelhança, também conhecido como Teorema da Semelhança por Retas Paralelas, é um princípio importante que relaciona a semelhança de triângulos com retas paralelas:

"Se uma reta é paralela a um lado de um triângulo e intercepta os outros dois lados, então ela determina um triângulo semelhante ao triângulo original."

Em outras palavras, se traçarmos uma reta paralela a um dos lados de um triângulo, cortando os outros dois lados, formaremos um novo triângulo que é semelhante ao triângulo original.

Este teorema é uma aplicação direta do Teorema de Tales e tem inúmeras aplicações práticas. Ele nos permite dividir os lados de um triângulo em segmentos proporcionais e é fundamental para muitas construções geométricas.

Exemplo: No triângulo ABC, se traçarmos uma reta DE paralela ao lado BC, com D no lado AB e E no lado AC, então o triângulo ADE é semelhante ao triângulo ABC.

Além disso, temos as seguintes relações:

• AD/AB = AE/AC = DE/BC

Esta é uma ferramenta poderosa para resolver problemas envolvendo proporções em triângulos.

Semelhança de Triângulos Retângulos

Os triângulos retângulos apresentam casos especiais de semelhança que merecem atenção particular, devido à sua frequente aplicação em problemas práticos.

Semelhança pela Altura Relativa à Hipotenusa

Em um triângulo retângulo, se traçarmos a altura relativa à hipotenusa, obtemos três triângulos retângulos semelhantes:

1. O triângulo original

2. O triângulo formado pela altura e um dos segmentos da hipotenusa

3. O triângulo formado pela altura e o outro segmento da hipotenusa

Esta propriedade é extremamente útil e está relacionada com o Teorema de Pitágoras. De fato, uma das demonstrações do Teorema de Pitágoras utiliza justamente a semelhança desses triângulos.

Relações Métricas no Triângulo Retângulo

A semelhança de triângulos nos permite estabelecer várias relações métricas importantes em triângulos retângulos:

1. O quadrado da altura relativa à hipotenusa é igual ao produto dos segmentos da hipotenusa: h² = m × n

2. O quadrado de um cateto é igual ao produto da hipotenusa pelo segmento adjacente: a² = c × m e b² = c × n

Onde:

• a e b são os catetos

• c é a hipotenusa

• h é a altura relativa à hipotenusa

• m e n são os segmentos da hipotenusa determinados pela altura

Estas relações são extremamente úteis para calcular elementos desconhecidos em triângulos retângulos.

Aplicações Práticas da Semelhança de Triângulos

A semelhança de triângulos não é apenas um conceito teórico; ela tem inúmeras aplicações práticas em nosso dia a dia:

Medição de Alturas Inacessíveis

Um dos usos mais antigos e práticos da semelhança de triângulos é a medição de alturas inacessíveis, como prédios, árvores ou montanhas. Utilizando as sombras projetadas ou técnicas de visada, podemos criar triângulos semelhantes e calcular alturas que seriam difíceis de medir diretamente.

Exemplo: Para medir a altura de um prédio, podemos usar uma vara de comprimento conhecido, medir sua sombra e a sombra do prédio no mesmo momento do dia. Pela semelhança de triângulos, a razão entre as alturas será igual à razão entre os comprimentos das sombras.

Cartografia e Mapas

A semelhança de triângulos é fundamental na cartografia para criar mapas em escala. Quando um mapa representa uma região, todos os triângulos no mapa são semelhantes aos triângulos correspondentes no terreno real, com uma razão de semelhança constante (a escala do mapa).

Fotografia e Projeções

Na fotografia, a semelhança de triângulos explica como as imagens são formadas nas câmeras. Os raios de luz formam triângulos semelhantes que relacionam o objeto real, a lente e a imagem projetada.

Arquitetura e Design

Arquitetos e designers usam a semelhança de triângulos para criar modelos em escala, garantindo que as proporções sejam mantidas quando uma estrutura é ampliada ou reduzida.

Triangulação em GPS

Os sistemas de GPS utilizam princípios de triangulação que se baseiam em semelhança de triângulos para determinar posições precisas na superfície terrestre.

Como Resolver Problemas Usando Semelhança de Triângulos

Para aplicar a semelhança de triângulos na resolução de problemas, podemos seguir uma abordagem sistemática:

1. Identificar os Triângulos Semelhantes

O primeiro passo é identificar os triângulos que são semelhantes no problema. Isso pode ser feito verificando um dos critérios de semelhança (AA, LAL ou LLL).

2. Estabelecer a Correspondência entre os Elementos

Uma vez identificados os triângulos semelhantes, é importante estabelecer claramente quais vértices, lados e ângulos correspondem entre si. Uma boa prática é nomear os vértices de forma que vértices correspondentes ocupem a mesma posição nos nomes dos triângulos (por exemplo, ABC ~ DEF, onde A corresponde a D, B corresponde a E, e C corresponde a F).

3. Determinar a Razão de Semelhança

Calcule a razão de semelhança k dividindo o comprimento de um lado de um triângulo pelo comprimento do lado correspondente no outro triângulo.

4. Aplicar as Propriedades da Semelhança

Utilize as propriedades da semelhança para calcular os valores desconhecidos:

• Para lados: lado₁/lado₂ = k

• Para perímetros: perímetro₁/perímetro₂ = k

• Para áreas: área₁/área₂ = k²

• Para outros elementos: elemento₁/elemento₂ = k

5. Verificar a Solução

Sempre verifique se a solução encontrada faz sentido no contexto do problema e se satisfaz todas as condições dadas.

Relação com Outros Conceitos Matemáticos

A semelhança de triângulos está intimamente relacionada com vários outros conceitos matemáticos importantes:

Teorema de Tales

O Teorema de Tales, que trata da proporcionalidade de segmentos determinados por retas paralelas, é a base para muitos resultados sobre semelhança de triângulos. De fato, o critério AA de semelhança pode ser visto como uma consequência direta do Teorema de Tales.

Teorema de Pitágoras

Como mencionado anteriormente, a semelhança de triângulos fornece uma das demonstrações mais elegantes do Teorema de Pitágoras. Além disso, as relações métricas no triângulo retângulo, derivadas da semelhança, estão diretamente relacionadas com o Teorema de Pitágoras.

Trigonometria

A semelhança de triângulos é o fundamento da trigonometria. As razões trigonométricas (seno, cosseno, tangente) são definidas como razões entre lados de triângulos retângulos semelhantes.

Homotetia

A homotetia, uma transformação geométrica que amplia ou reduz figuras mantendo suas formas, está diretamente relacionada à semelhança. Dois triângulos semelhantes podem ser vistos como um sendo a imagem do outro por uma homotetia.

Geometria Analítica

Na geometria analítica, a semelhança de triângulos é utilizada para demonstrar propriedades de figuras no plano cartesiano e para resolver problemas envolvendo distâncias e proporções.

Conclusão: A Importância da Semelhança de Triângulos

A semelhança de triângulos é um dos conceitos mais fundamentais e versáteis da geometria. Desde os tempos antigos, quando Tales de Mileto usou princípios de semelhança para medir a altura da Grande Pirâmide, até os dias atuais, com aplicações em tecnologia GPS e design digital, este conceito continua sendo uma ferramenta matemática essencial.

O que torna a semelhança de triângulos tão especial é sua combinação de simplicidade conceitual e ampla aplicabilidade. Entender que dois triângulos podem ter a mesma forma, mas tamanhos diferentes, e que isso implica em relações proporcionais entre seus elementos, abre portas para resolver uma infinidade de problemas práticos e teóricos.

Ao dominar os critérios de semelhança e suas propriedades, você adquire uma ferramenta poderosa que permite calcular distâncias inacessíveis, compreender escalas e proporções, e estabelecer conexões entre diferentes áreas da matemática.

Agora que você compreende a semelhança de triângulos, suas propriedades, aplicações e como utilizá-la para resolver problemas, está pronto para praticar com os exercícios a seguir e consolidar seu aprendizado.

Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=lYEJ19G9fck

Canal: Gis com Giz Matemática

http://www.youtube.com/watch?v=JBP0ryUtJmg

Canal: Dicasdemat Sandro Curió