Exercícios:

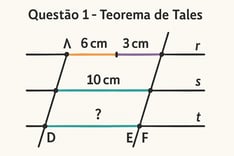
1. Na figura acima, as retas r, s e t são paralelas. Se AB = 6 cm e BC = 3 cm, e sabendo que DE = 10 cm, determine o valor de EF.

Respostas:

Resolução da Questão 1

Pelo Teorema de Tales, temos: AB/BC = DE/EF 6/3 = 10/EF 2 = 10/EF EF = 10/2 = 5 cm

Portanto, EF = 5 cm.

Resolução da Questão 2

Pelo Teorema de Tales, temos: AB/AC = DE/DF 8/12 = 6/DF 2/3 = 6/DF DF × (2/3) = 6 DF = 6 × (3/2) = 9 cm

Portanto, DF = 9 cm.

Resolução da Questão 3

Pelo Teorema de Tales, temos: AD/AB = AE/AC 9/15 = AE/20 3/5 = AE/20 AE = 20 × (3/5) = 12 cm

Portanto, AE = 12 cm.

Resolução da Questão 4

Pelo Teorema de Tales, devemos ter: AB/BC = DE/EF 4/6 = 8/12 2/3 = 2/3

Como as razões são iguais, o Teorema de Tales é satisfeito.

Resolução da Questão 5

Pelo Teorema de Tales, temos: AD/AB = AE/AC 8/12 = 10/AC 2/3 = 10/AC AC × (2/3) = 10 AC = 10 × (3/2) = 15 cm

Portanto, AC = 15 cm.

Resolução da Questão 6

Pelo Teorema de Tales, temos: AB/BC = DE/EF 9/6 = 12/x 3/2 = 12/x x × (3/2) = 12 x = 12 × (2/3) = 8 cm

Portanto, x = 8 cm.

Resolução da Questão 7

Pelo Teorema de Tales, temos: altura do poste / sombra do poste = altura do prédio / sombra do prédio 6/8 = h/40 3/4 = h/40 h = 40 × (3/4) = 30 metros

Portanto, a altura do prédio é de 30 metros.

Resolução da Questão 8

Pelo Teorema de Tales, temos: AD/AB = AE/AC 4/10 = x/15 2/5 = x/15 x = 15 × (2/5) = 6 cm

Portanto, x = 6 cm.

Resolução da Questão 9

Pelo Teorema de Tales, temos: AB/BC = DE/EF 5/7 = 10/EF EF = 10 × (7/5) = 14 cm

Portanto, EF = 14 cm.

Resolução da Questão 10

Pelo Teorema de Tales, temos: altura do fotógrafo / sombra do fotógrafo = altura do prédio / sombra do prédio 1,8/1,2 = h/20 3/2 = h/20 h = 20 × (3/2) = 30 metros

Portanto, a altura do prédio é de 30 metros.

Resolução da Questão 11

Pelo Teorema de Tales, temos: AB/BC = DE/EF 3/2 = 9/x x = 9 × (2/3) = 6 cm

Portanto, x = 6 cm.

Resolução da Questão 12

Pelo Teorema de Tales, temos: AD/AB = AE/AC 12/18 = AE/27 2/3 = AE/27 AE = 27 × (2/3) = 18 cm

Portanto, AE = 18 cm.

Resolução da Questão 13

Pelo Teorema de Tales, temos: AB/BC = DE/EF 10/5 = 6/EF 2 = 6/EF EF = 6/2 = 3 cm

Portanto, EF = 3 cm.

Resolução da Questão 14

Pelo Teorema de Tales, temos: altura do homem / sombra do homem = altura do poste / sombra do poste 1,75/2,5 = h/12 7/10 = h/12 h = 12 × (7/10) = 8,4 metros

Portanto, a altura do poste é de 8,4 metros.

Resolução da Questão 15

Primeiro, pelo Teorema de Tales, temos: AD/AB = AE/AC 8/24 = AE/AC 1/3 = AE/AC AE = AC/3

Agora, como DF é paralelo a AC, temos outro caso do Teorema de Tales: AD/AB = DF/BC 8/24 = 5/BC 1/3 = 5/BC BC = 15 cm

Como DE é paralelo a BC, temos: AD/AB = DE/BC 8/24 = DE/15 1/3 = DE/15 DE = 5 cm

Finalmente, como DE = 5 cm e AE = AC/3, e sabendo que DF = 5 cm é paralelo a AC, podemos concluir que AC = 15 cm.

Portanto, AC = 15 cm.

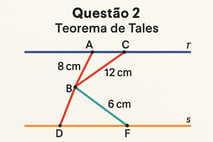
2. Na figura acima, as retas r e s são paralelas. Se AB = 8 cm, AC = 12 cm, e DE = 6 cm, determine o valor de DF.

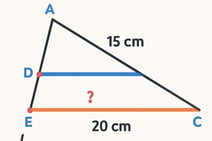
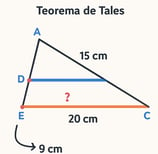
3. No triângulo ABC, o ponto D está no lado AB e o ponto E está no lado AC, de modo que DE é paralelo a BC. Se AB = 15 cm, AD = 9 cm, AC = 20 cm, determine o valor de AE.

4. As retas r, s e t são paralelas. Se AB = 4 cm, BC = 6 cm, DE = 8 cm, e EF = 12 cm, verifique se o Teorema de Tales é satisfeito.

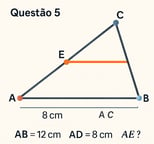
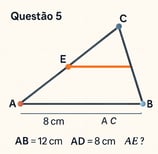
5. No triângulo ABC, o ponto D está no lado AB e o ponto E está no lado AC, de modo que DE é paralelo a BC. Se AB = 12 cm, AD = 8 cm, e AE = 10 cm, determine o valor de AC.

6. Na figura abaixo, as retas r e s são paralelas. Se AB = 9 cm, BC = 6 cm, DE = 12 cm, e EF = x cm, determine o valor de x.

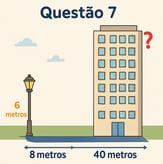
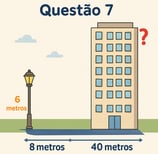
7. Um poste de 6 metros de altura projeta uma sombra de 8 metros. No mesmo instante, um prédio próximo projeta uma sombra de 40 metros. Qual é a altura do prédio?

8. No triângulo ABC, os pontos D e E estão nos lados AB e AC, respectivamente, de modo que DE é paralelo a BC. Se AB = 10 cm, AD = 4 cm, AC = 15 cm, e AE = x cm, determine o valor de x.

9. Na figura abaixo, as retas r, s e t são paralelas. Se AB = 5 cm, BC = 7 cm, e DE = 10 cm, determine o valor de EF.

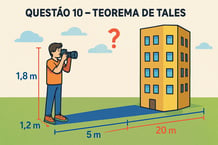
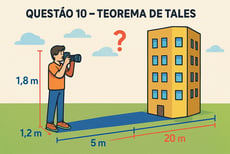
10. Um fotógrafo de 1,8 metros de altura está a 5 metros de distância de um prédio. Ele observa que sua sombra tem 1,2 metros de comprimento, enquanto a sombra do prédio tem 20 metros. Qual é a altura do prédio?

11. Na figura abaixo, as retas r, s e t são paralelas. Se AB = 3 cm, BC = 2 cm, DE = 9 cm, e EF = x cm, determine o valor de x.

12. No triângulo ABC, o ponto D está no lado AB e o ponto E está no lado AC, de modo que DE é paralelo a BC. Se AB = 18 cm, AD = 12 cm, AC = 27 cm, determine o valor de AE.1

13. Na figura abaixo, as retas r e s são paralelas. Se AB = 10 cm, BC = 5 cm, e DE = 6 cm, determine o valor de EF.

14. Um homem de 1,75 metros de altura está a uma certa distância de um poste. No mesmo instante em que a sombra do homem mede 2,5 metros, a sombra do poste mede 12 metros. Qual é a altura do poste?

15. No triângulo ABC, os pontos D, E e F estão nos lados AB, AC e BC, respectivamente, de modo que DE é paralelo a BC e DF é paralelo a AC. Se AB = 24 cm, AD = 8 cm, e DF = 5 cm, determine o valor de AC.