Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=RKegZ1TiO28

Canal: Gis com Giz Matemática

http://www.youtube.com/watch?v=yHxkyYFy-Eg

Canal: Dicasdemat Sandro Curió

Teorema de Tales Desvendado: Guia Completo com Imagens para o Ensino Fundamental

Você já se perguntou como medir a altura de um prédio sem subir nele? Ou como os antigos conseguiam calcular a altura das pirâmides? A resposta para essas e muitas outras questões está no Teorema de Tales, um dos princípios mais importantes e práticos da geometria.

Neste artigo, vamos desvendar todos os segredos desse teorema fascinante, com explicações simples, exemplos práticos e muitas imagens para facilitar seu entendimento. Prepare-se para descobrir como a matemática pode ser surpreendentemente útil no dia a dia!

Quem foi Tales de Mileto e Como Surgiu o Teorema?

Tales de Mileto foi um matemático, filósofo e astrônomo grego que viveu entre 624 a.C. e 546 a.C. Considerado um dos "Sete Sábios da Grécia Antiga", ele é frequentemente chamado de "Pai da Filosofia Ocidental" e também deu contribuições fundamentais para a matemática.

Uma das histórias mais famosas sobre Tales conta como ele conseguiu medir a altura da Grande Pirâmide de Quéops, no Egito, sem precisar escalá-la. Ele observou que, em determinado momento do dia, quando sua própria sombra tinha exatamente o mesmo comprimento que sua altura, a sombra de qualquer objeto seria proporcional à sua altura.

Assim, Tales mediu a sombra da pirâmide nesse momento específico e, com isso, determinou sua altura. Esse método engenhoso demonstra o princípio fundamental do que viria a ser conhecido como Teorema de Tales: a proporcionalidade entre segmentos de reta.

O que é o Teorema de Tales?

O Teorema de Tales pode ser enunciado da seguinte forma:

"Um feixe de retas paralelas determina, sobre duas retas transversais quaisquer, segmentos proporcionais."

Isso pode parecer complicado à primeira vista, mas vamos simplificar. Imagine várias linhas paralelas (como as linhas de um caderno) sendo cortadas por duas retas não paralelas entre si. O teorema nos diz que os segmentos formados em uma das retas transversais são proporcionais aos segmentos correspondentes na outra reta transversal.

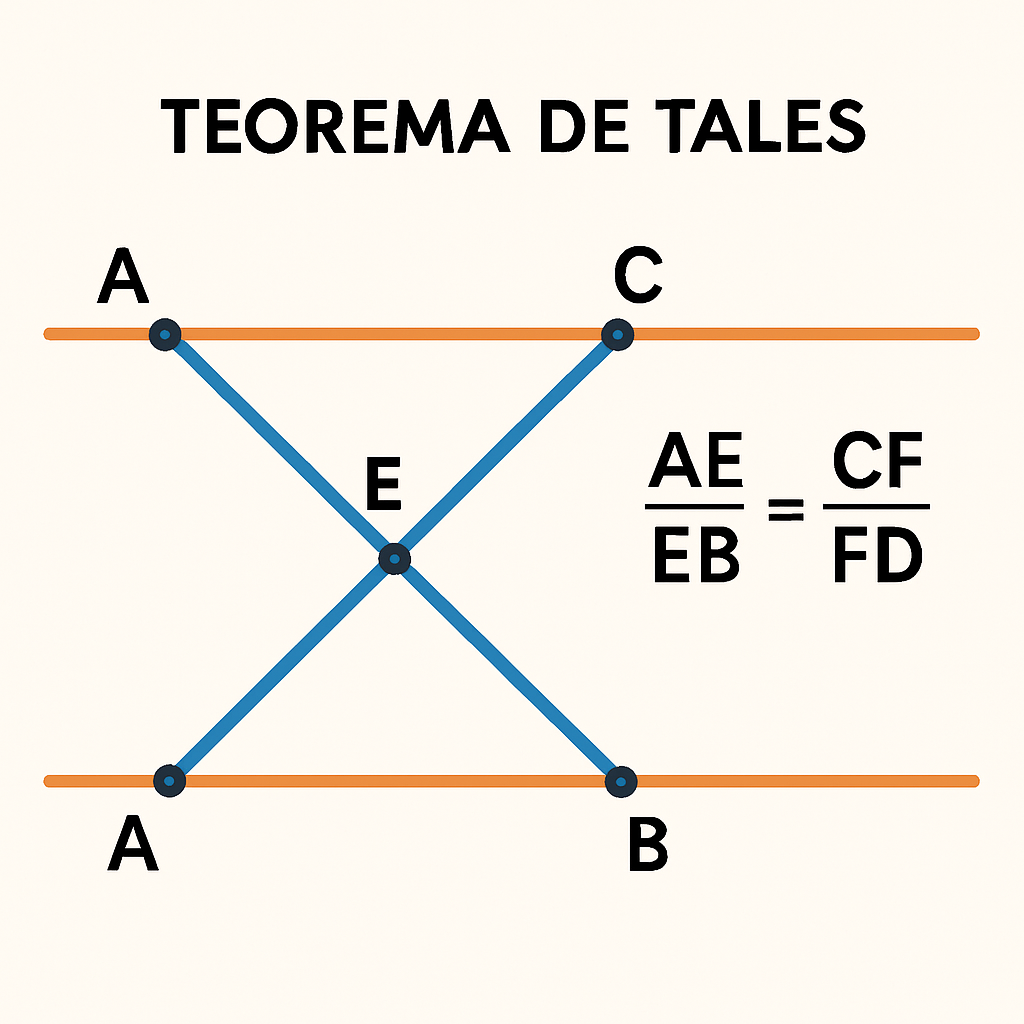
Observando a imagem acima, podemos expressar matematicamente o Teorema de Tales da seguinte forma:

AE/EB = CF/FD

Ou seja, a razão entre os segmentos AE e EB é igual à razão entre os segmentos CF e FD.

Demonstração do Teorema de Tales

Para entender melhor o Teorema de Tales, vamos ver como ele pode ser demonstrado de forma simples.

Considere duas retas transversais cortadas por três retas paralelas, formando os pontos A, B e C na primeira transversal e D, E e F na segunda transversal.

Para demonstrar que AB/BC = DE/EF, podemos usar o conceito de semelhança de triângulos:

1. Traçamos uma linha auxiliar ligando os pontos A e D.

2. Traçamos linhas paralelas a AD passando por B e C.

3. Essas linhas paralelas interceptam a reta que contém D, E e F nos pontos E e F.

4. Formam-se triângulos semelhantes.

5. Por semelhança de triângulos, temos que AB/BC = DE/EF.

Esta demonstração nos mostra que o Teorema de Tales está intimamente relacionado com a semelhança de triângulos, outro conceito fundamental da geometria.

Aplicações do Teorema de Tales na Geometria

Uma das aplicações mais importantes do Teorema de Tales é na geometria, especialmente quando trabalhamos com triângulos.

Teorema de Tales em Triângulos

Quando traçamos uma reta paralela a um dos lados de um triângulo, interceptando os outros dois lados, formamos um triângulo menor que é semelhante ao triângulo original.

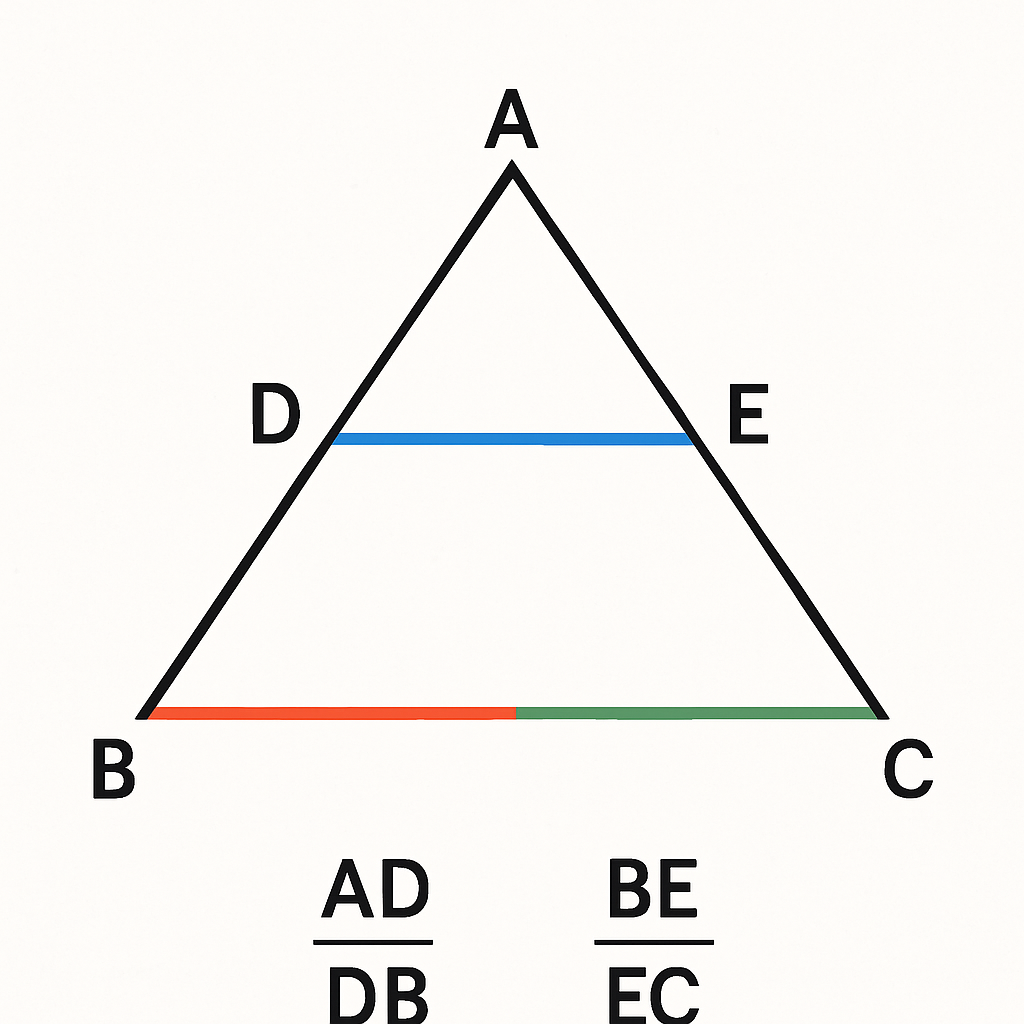
Na figura acima, a reta DE é paralela à base BC do triângulo ABC. Pelo Teorema de Tales, podemos afirmar que:

AD/AB = AE/AC

Isso significa que os segmentos determinados nos lados do triângulo são proporcionais. Esta propriedade é extremamente útil para calcular medidas desconhecidas em triângulos.

Divisão Proporcional de Segmentos

O Teorema de Tales também nos permite dividir um segmento em partes proporcionais. Por exemplo, se quisermos dividir um segmento AB em três partes iguais, podemos:

1. Traçar uma semirreta com origem em A, formando um ângulo qualquer com AB.

2. Marcar três pontos equidistantes nessa semirreta: P, Q e R.

3. Ligar R a B.

4. Traçar retas paralelas a RB passando por P e Q.

5. Essas paralelas interceptarão AB nos pontos que o dividem em três partes iguais.

Esta aplicação é muito útil em desenho técnico, arquitetura e outras áreas que exigem precisão nas medidas.

Aplicações Práticas do Teorema de Tales no Cotidiano

O Teorema de Tales não é apenas um conceito teórico; ele tem muitas aplicações práticas no nosso dia a dia.

Medição de Alturas Inacessíveis

Assim como Tales mediu a altura da pirâmide, podemos usar o mesmo princípio para medir a altura de prédios, árvores ou outros objetos altos sem precisar subir neles.

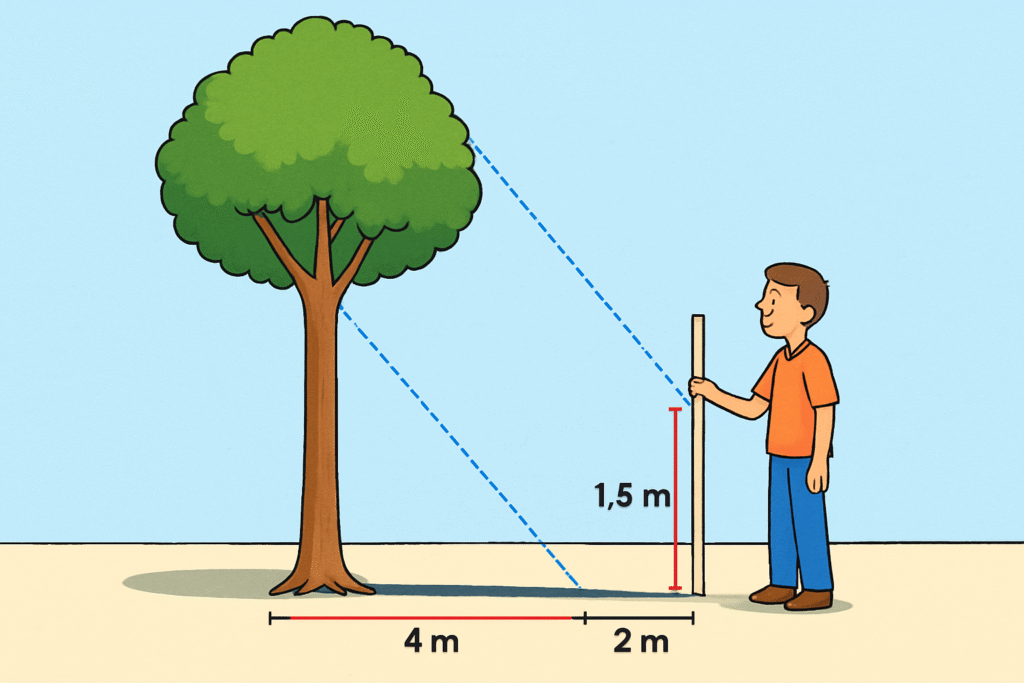
Na imagem acima, vemos como podemos medir a altura de uma árvore usando uma vara de comprimento conhecido e as sombras projetadas. Se a vara tem 1,5 metros de altura e projeta uma sombra de 2 metros, enquanto a árvore projeta uma sombra de 4 metros, podemos calcular a altura da árvore (h) usando a proporção:

1,5/2 = h/4

Resolvendo: h = 4 × (1,5/2) = 4 × 0,75 = 3 metros

Portanto, a árvore tem 3 metros de altura.

Aplicações na Arquitetura e Engenharia

Na arquitetura e engenharia, o Teorema de Tales é usado para:

• Criar plantas em escala

• Calcular distâncias inacessíveis

• Projetar estruturas proporcionais

• Determinar a inclinação de rampas e telhados

Aplicações na Arte e Design

Na arte e design, o teorema é aplicado para:

• Criar perspectivas realistas em desenhos

• Redimensionar imagens mantendo as proporções

• Desenvolver layouts harmoniosos

• Criar padrões geométricos proporcionais

Como Resolver Problemas Usando o Teorema de Tales

Resolver problemas com o Teorema de Tales segue geralmente um processo de quatro passos:

1. Identificar as retas paralelas e transversais: Reconheça o padrão do Teorema de Tales no problema.

2. Estabelecer a proporção: Escreva a equação de proporcionalidade entre os segmentos correspondentes.

3. Substituir os valores conhecidos: Coloque os valores dados no problema na equação.

4. Resolver a equação: Encontre o valor desconhecido usando operações algébricas.

Exemplo Resolvido

Vamos resolver um exemplo prático:

Problema: Na figura abaixo, as retas r, s e t são paralelas. Se AB = 8 cm, BC = 4 cm, DE = 6 cm, qual é o valor de EF?

Solução:

1. Identificamos que temos retas paralelas (r, s e t) cortadas por duas transversais.

2. Pelo Teorema de Tales, temos: AB/BC = DE/EF

3. Substituindo os valores: 8/4 = 6/EF

4. Simplificando: 2 = 6/EF

5. Multiplicando ambos os lados por EF: 2 × EF = 6

6. Dividindo ambos os lados por 2: EF = 3 cm

Portanto, EF = 3 cm.

Dicas para Aplicar o Teorema de Tales Corretamente

Para aplicar o Teorema de Tales com sucesso, lembre-se destas dicas:

1. Verifique o paralelismo: O teorema só funciona quando as retas são realmente paralelas.

2. Mantenha a ordem correta: Ao estabelecer a proporção, certifique-se de que os segmentos correspondentes estão na mesma ordem.

3. Simplifique frações: Sempre que possível, simplifique as frações para facilitar os cálculos.

4. Faça um desenho claro: Um diagrama bem feito ajuda a visualizar o problema e evitar erros.

5. Verifique sua resposta: Substitua o valor encontrado na equação original para confirmar se está correto.

A Importância do Teorema de Tales na Matemática

O Teorema de Tales é um dos pilares da geometria euclidiana e serve como base para muitos outros conceitos matemáticos importantes, como:

• Semelhança de triângulos

• Teorema de Pitágoras

• Trigonometria

• Geometria analítica

• Cálculo de áreas e volumes

Além disso, ele nos mostra como a matemática pode ser uma ferramenta poderosa para resolver problemas práticos do mundo real, conectando conceitos abstratos com aplicações concretas.

Conclusão: Por Que o Teorema de Tales é Tão Importante?

O Teorema de Tales é um exemplo perfeito de como a matemática pode ser ao mesmo tempo elegante em sua simplicidade e poderosa em suas aplicações. Desde a antiguidade até os dias atuais, este teorema continua sendo uma ferramenta fundamental para resolver problemas geométricos e do mundo real.

Ao dominar o Teorema de Tales, você não está apenas aprendendo uma fórmula matemática, mas adquirindo uma forma de pensar que permite enxergar proporções e relações em diversos contextos. É um conhecimento que transcende a sala de aula e encontra aplicações em praticamente todas as áreas que envolvem medidas e proporções.

Agora que você compreende o Teorema de Tales, suas origens, aplicações e como utilizá-lo, está pronto para resolver os exercícios a seguir e consolidar seu aprendizado.