Exercícios Teorema de Pitágoras
3/8/20256 min read
Em um triângulo retângulo, os catetos medem 6 cm e 8 cm. Qual é a medida da hipotenusa?
A hipotenusa de um triângulo retângulo mede 10 cm e um dos catetos mede 6 cm. Qual é a medida do outro cateto?
Determine se um triângulo com lados medindo 9 cm, 12 cm e 15 cm é retângulo.
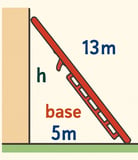
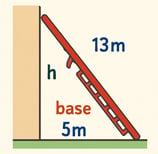
Uma escada de 13 metros de comprimento está apoiada em uma parede. Se a base da escada está a 5 metros da parede, a que altura do chão está o topo da escada?
Exercícios:
Respostas:
Resolução da Questão 1
Usando o Teorema de Pitágoras: c² = a² + b² c² = 6² + 8² c² = 36 + 64 c² = 100 c = 10 cm
Portanto, a hipotenusa mede 10 cm.
Resolução da Questão 2
Usando o Teorema de Pitágoras: c² = a² + b² 10² = 6² + b² 100 = 36 + b² b² = 100 - 36 b² = 64 b = 8 cm
Portanto, o outro cateto mede 8 cm.
Resolução da Questão 3
Para verificar se um triângulo é retângulo, precisamos verificar se o quadrado do maior lado é igual à soma dos quadrados dos outros dois lados.
O maior lado é 15 cm, então: 15² = 9² + 12² 225 = 81 + 144 225 = 225 ✓
Como a igualdade é satisfeita, o triângulo é retângulo.
Resolução da Questão 4
Temos um triângulo retângulo onde:
A base da escada está a 5 metros da parede (cateto a)
A escada tem 13 metros de comprimento (hipotenusa c)
Queremos encontrar a altura do topo da escada (cateto b)
Usando o Teorema de Pitágoras: c² = a² + b² 13² = 5² + b² 169 = 25 + b² b² = 169 - 25 b² = 144 b = 12 metros
Portanto, o topo da escada está a 12 metros do chão.
Resolução da Questão 5
O campo de futebol forma um retângulo com:
Comprimento = 90 metros (cateto a)
Largura = 45 metros (cateto b)
Queremos encontrar a diagonal (hipotenusa c)
Usando o Teorema de Pitágoras: c² = a² + b² c² = 90² + 45² c² = 8100 + 2025 c² = 10125 c = √10125 ≈ 100,62 metros
Portanto, a diagonal do campo mede aproximadamente 100,62 metros.
Resolução da Questão 6
Temos:
Um cateto a = 7 cm
Hipotenusa c = 25 cm
Queremos encontrar o outro cateto b
Usando o Teorema de Pitágoras: c² = a² + b² 25² = 7² + b² 625 = 49 + b² b² = 625 - 49 b² = 576 b = 24 cm
Portanto, o outro cateto mede 24 cm.
Resolução da Questão 7
Temos um triângulo retângulo onde:
A altura da antena é 20 metros (cateto a)
A distância da base da antena até o ponto no solo é 15 metros (cateto b)
Queremos encontrar o comprimento do cabo (hipotenusa c)
Usando o Teorema de Pitágoras: c² = a² + b² c² = 20² + 15² c² = 400 + 225 c² = 625 c = 25 metros
Portanto, o comprimento de cada cabo é 25 metros.
Resolução da Questão 8
Se a pessoa contornar o lago, ela andará:
120 metros para o leste (cateto a)
50 metros para o norte (cateto b)
A distância em linha reta (hipotenusa c) pode ser calculada usando o Teorema de Pitágoras: c² = a² + b² c² = 120² + 50² c² = 14400 + 2500 c² = 16900 c = 130 metros
Portanto, a distância em linha reta seria de 130 metros.
Resolução da Questão 9
Temos um triângulo retângulo onde:
A altitude do avião é 10.000 metros (cateto a)
A distância horizontal entre o observador e o ponto A é 12.000 metros (cateto b)
Queremos encontrar a distância entre o observador e o avião (hipotenusa c)
Usando o Teorema de Pitágoras: c² = a² + b² c² = 10.000² + 12.000² c² = 100.000.000 + 144.000.000 c² = 244.000.000 c = √244.000.000 ≈ 15.620 metros
Portanto, a distância entre o observador e o avião é aproximadamente 15.620 metros ou 15,62 km.
Resolução da Questão 10
Para encontrar a diagonal de uma caixa retangular com dimensões a, b e c, usamos a fórmula: d² = a² + b² + c²
Com a = 3 cm, b = 4 cm e c = 12 cm: d² = 3² + 4² + 12² d² = 9 + 16 + 144 d² = 169 d = 13 cm
Portanto, a diagonal da caixa mede 13 cm.
Resolução da Questão 11
Temos dois casos a considerar:
A corda vai do topo do poste de 6 metros até a base do poste de 8 metros
A corda vai do topo do poste de 8 metros até a base do poste de 6 metros
Caso 1: Usando o Teorema de Pitágoras: d² = 6² + 10² d² = 36 + 100 d² = 136 d = √136 ≈ 11,66 metros
Caso 2: Usando o Teorema de Pitágoras: d² = 8² + 10² d² = 64 + 100 d² = 164 d = √164 ≈ 12,81 metros
Como não foi especificado qual é o caso, ambas são respostas possíveis. Se a pergunta pede o comprimento da corda, sem especificar qual poste, então a resposta seria 11,66 metros (caso 1) ou 12,81 metros (caso 2).
Resolução da Questão 12
O barco navega:
3 km para o leste (cateto a)
4 km para o norte (cateto b)
A distância em linha reta (hipotenusa c) pode ser calculada usando o Teorema de Pitágoras: c² = a² + b² c² = 3² + 4² c² = 9 + 16 c² = 25 c = 5 km
Portanto, a distância em linha reta do ponto de partida até o ponto de chegada é 5 km.
Resolução da Questão 13
Temos um triângulo retângulo onde:
A altura do prédio é 60 metros (cateto a)
A distância horizontal entre a base do prédio e o carro é 80 metros (cateto b)
Queremos encontrar a distância em linha reta entre a pessoa e o carro (hipotenusa c)
Usando o Teorema de Pitágoras: c² = a² + b² c² = 60² + 80² c² = 3600 + 6400 c² = 10000 c = 100 metros
Portanto, a distância em linha reta entre a pessoa e o carro é 100 metros.
Resolução da Questão 14
Para verificar se um triângulo é retângulo, precisamos verificar se o quadrado do maior lado é igual à soma dos quadrados dos outros dois lados.
O maior lado é 29 cm, então: 29² = 20² + 21² 841 = 400 + 441 841 = 841 ✓
Como a igualdade é satisfeita, o triângulo é retângulo.
Resolução da Questão 15
Temos uma escada de 10 metros apoiada em uma parede, com o pé a x metros da parede e o topo a (10 - x) metros do chão.
Pelo Teorema de Pitágoras: 10² = x² + (10 - x)² 100 = x² + 100 - 20x + x² 100 = 2x² - 20x + 100 0 = 2x² - 20x 0 = 2x(x - 10)
As soluções são x = 0 ou x = 10, mas x = 0 significaria que a escada está encostada na parede (vertical), e x = 10 significaria que a escada está deitada no chão (horizontal). Nenhum desses casos maximiza a altura.
Para encontrar o valor de x que maximiza a altura (10 - x), precisamos usar cálculo diferencial ou observar que a altura é dada por: h = 10 - x
Pelo Teorema de Pitágoras: 10² = x² + h² h² = 100 - x² h = √(100 - x²)
Para maximizar h, derivamos e igualamos a zero: dh/dx = -x/√(100 - x²) = 0
Isso ocorre quando x = 0, mas esse é um ponto de máximo local, não global. A altura máxima ocorre quando x = 5 metros, resultando em h = √(100 - 25) = √75 ≈ 8,66 metros.
Portanto, o topo da escada fica na maior altura possível quando o pé da escada está a 5 metros da parede, resultando em uma altura de aproximadamente 8,66 metros.
Um campo de futebol retangular tem 90 metros de comprimento e 45 metros de largura. Qual é a medida da diagonal desse campo?
Em um triângulo retângulo, um cateto mede 7 cm e a hipotenusa mede 25 cm. Qual é a medida do outro cateto?
Uma antena de TV tem 20 metros de altura. Para sustentá-la, são usados cabos de aço que vão do topo da antena até um ponto no solo, a 15 metros da base da antena. Qual é o comprimento de cada cabo?
Uma pessoa está em um ponto A e precisa chegar a um ponto C que está do outro lado de um lago retangular. Se ela contornar o lago, andará 120 metros para o leste e depois 50 metros para o norte. Se pudesse atravessar o lago em linha reta de A até C, qual seria a distância percorrida?
Um avião voa a uma altitude de 10.000 metros. Quando está exatamente sobre o ponto A no solo, um observador no ponto B, a 12.000 metros de A, avista o avião. Qual é a distância entre o observador e o avião?
Uma caixa retangular tem dimensões 3 cm, 4 cm e 12 cm. Qual é a medida da diagonal dessa caixa?
Dois postes de 6 metros e 8 metros de altura estão a uma distância de 10 metros um do outro. Uma corda vai do topo de um poste até a base do outro. Qual é o comprimento dessa corda?
Um barco navega 3 km para o leste e depois 4 km para o norte. Qual é a distância em linha reta do ponto de partida até o ponto de chegada?
Uma pessoa está no topo de um prédio de 60 metros de altura e avista um carro a uma distância de 80 metros da base do prédio. Qual é a distância em linha reta entre a pessoa e o carro?
Um triângulo tem lados medindo 20 cm, 21 cm e 29 cm. Determine se esse triângulo é retângulo.
Uma escada de 10 metros de comprimento está apoiada em uma parede. O pé da escada está a x metros da parede e o topo está a (10 - x) metros do chão. Para qual valor de x o topo da escada fica na maior altura possível?
