Teorema de Pitágoras
Teorema de Pitágoras Desvendado
Você já se perguntou como os engenheiros calculam a distância exata entre dois pontos? Ou como os arquitetos conseguem projetar estruturas perfeitamente alinhadas? A resposta para essas e muitas outras questões está no Teorema de Pitágoras, um dos princípios mais importantes e versáteis da matemática.
Neste artigo, vamos explorar todos os aspectos desse teorema fascinante, com explicações simples, exemplos práticos e imagens ilustrativas para facilitar seu entendimento. Prepare-se para descobrir como um conceito matemático de mais de 2500 anos continua sendo fundamental em nosso dia a dia!
Quem foi Pitágoras e a História do Teorema

Pitágoras foi um matemático e filósofo grego que viveu entre 570 a.C. e 495 a.C. Nascido na ilha de Samos, ele fundou uma escola filosófica e religiosa na cidade de Crotona, no sul da Itália, conhecida como Escola Pitagórica.
Embora o teorema que leva seu nome seja sua contribuição mais famosa para a matemática, existem evidências de que civilizações anteriores, como os babilônios e egípcios, já conheciam relações semelhantes. No entanto, Pitágoras é creditado por ter sido o primeiro a demonstrá-lo matematicamente.
A Escola Pitagórica era uma comunidade que estudava não apenas matemática, mas também música, astronomia e filosofia. Os membros acreditavam que “tudo é número” e que a matemática era a chave para compreender o universo. Eles mantinham seus conhecimentos em segredo, e os membros juravam não revelar as descobertas matemáticas fora do grupo.
Uma curiosidade interessante é que, segundo a lenda, Pitágoras ficou tão feliz ao descobrir seu famoso teorema que ofereceu um sacrifício de 100 bois aos deuses. Por isso, às vezes, grandes descobertas matemáticas são chamadas de “hecatombes”, palavra que significa “sacrifício de 100 bois”.
O que é o Teorema de Pitágoras
O Teorema de Pitágoras pode ser enunciado de forma simples:
“Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.”
Em termos matemáticos, se chamarmos a hipotenusa de c e os catetos de a e b, podemos escrever:
c^2 = a^2 + b^2
Mas o que isso significa na prática? Um triângulo retângulo é aquele que possui um ângulo reto (90°). A hipotenusa é o lado oposto ao ângulo reto, e é sempre o lado mais longo do triângulo. Os catetos são os outros dois lados, que formam o ângulo reto.
O teorema nos diz que se elevarmos ao quadrado o comprimento da hipotenusa, obteremos o mesmo valor que a soma dos quadrados dos comprimentos dos catetos. Esta relação é válida para qualquer triângulo retângulo, independentemente de seu tamanho.
Por exemplo, se um triângulo retângulo tem catetos medindo 3 cm e 4 cm, a hipotenusa (c) pode ser calculada assim:
c^2 = 3^2 + 4^2 c^2 = 9 + 16 c^2 = 25 c = 5 cm
Portanto, a hipotenusa mede 5 cm.
Demonstrações Visuais do Teorema de Pitágoras
Uma das belezas do Teorema de Pitágoras é que ele pode ser demonstrado de várias maneiras. Vamos explorar algumas demonstrações visuais que tornam esse conceito mais tangível.
Demonstração por Áreas de Quadrados
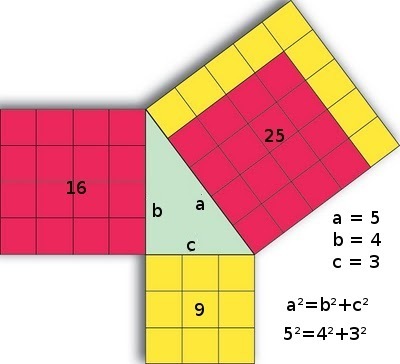
A demonstração mais conhecida envolve a comparação das áreas de quadrados construídos sobre os lados do triângulo retângulo.
Imagine um triângulo retângulo com catetos a e b, e hipotenusa c. Se construirmos quadrados sobre cada um desses lados, o quadrado sobre a hipotenusa terá área c^2, e os quadrados sobre os catetos terão áreas a^2 e b^2, respectivamente.
O Teorema de Pitágoras afirma que a área do quadrado maior (sobre a hipotenusa) é igual à soma das áreas dos dois quadrados menores (sobre os catetos).
Demonstração por Decomposição
Outra demonstração elegante envolve a decomposição e rearranjo de áreas:
Começamos com um quadrado de lado (a + b).
Dentro desse quadrado, construímos quatro triângulos retângulos idênticos, cada um com catetos a e b, e hipotenusa c.
Os triângulos são dispostos de modo que formem um quadrado menor no centro, cujo lado é a hipotenusa c.
A área do quadrado grande é (a + b)^2 = a^2 + 2ab + b^2.
A mesma área pode ser calculada como a soma da área do quadrado central (c^2) e as áreas dos quatro triângulos (4 × (a × b)/2 = 2ab).
Igualando as duas expressões: a^2 + 2ab + b^2 = c^2 + 2ab
Simplificando: a^2 + b^2 = c^2
Esta demonstração mostra visualmente como as áreas se relacionam, tornando o teorema mais intuitivo.
Demonstração por Semelhança de Triângulos
Uma terceira demonstração utiliza o conceito de semelhança de triângulos:
Traçamos a altura h do triângulo retângulo, partindo do ângulo reto até a hipotenusa.
Isso divide o triângulo original em dois triângulos menores, ambos semelhantes ao triângulo original e semelhantes entre si.
Usando as propriedades de triângulos semelhantes, podemos estabelecer proporções que, quando manipuladas algebricamente, nos levam à fórmula c^2 = a^2 + b^2.
Estas demonstrações visuais ajudam a compreender por que o Teorema de Pitágoras funciona, além de apenas memorizar a fórmula.
Como Aplicar o Teorema de Pitágoras
Aplicar o Teorema de Pitágoras é relativamente simples, mas requer atenção aos detalhes. Vamos ver como utilizá-lo em diferentes situações:
Calculando a Hipotenusa
Quando conhecemos os dois catetos (a e b) e queremos encontrar a hipotenusa (c):
Eleve cada cateto ao quadrado: a^2 e b^2
Some os resultados: a^2 + b^2
Extraia a raiz quadrada da soma: c = √(a^2 + b^2)
Exemplo: Se os catetos medem 6 cm e 8 cm, a hipotenusa será: c = √(6^2 + 8^2) = √(36 + 64) = √100 = 10 cm
Calculando um Cateto
Quando conhecemos a hipotenusa (c) e um cateto (a) e queremos encontrar o outro cateto (b):
Eleve a hipotenusa ao quadrado: c^2
Eleve o cateto conhecido ao quadrado: a^2
Subtraia o quadrado do cateto do quadrado da hipotenusa: c^2 – a^2
Extraia a raiz quadrada da diferença: b = √(c^2 – a^2)
Exemplo: Se a hipotenusa mede 13 cm e um cateto mede 5 cm, o outro cateto será: b = √(13^2 – 5^2) = √(169 – 25) = √144 = 12 cm
Verificando se um Triângulo é Retângulo
O Teorema de Pitágoras também pode ser usado para verificar se um triângulo é retângulo. Se tivermos três lados a, b e c (onde c é o maior lado), o triângulo é retângulo se e somente se: c^2 = a^2 + b^2
Exemplo: Um triângulo com lados 5 cm, 12 cm e 13 cm é retângulo porque: 13^2 = 5^2 + 12^2 169 = 25 + 144 169 = 169 ✓
Triângulos Pitagóricos e Ternos Notáveis
Os triângulos pitagóricos são triângulos retângulos cujos lados têm medidas que são números inteiros. Os ternos pitagóricos são conjuntos de três números inteiros positivos (a, b, c) que satisfazem a equação a^2 + b^2 = c^2.
Alguns ternos pitagóricos famosos incluem:
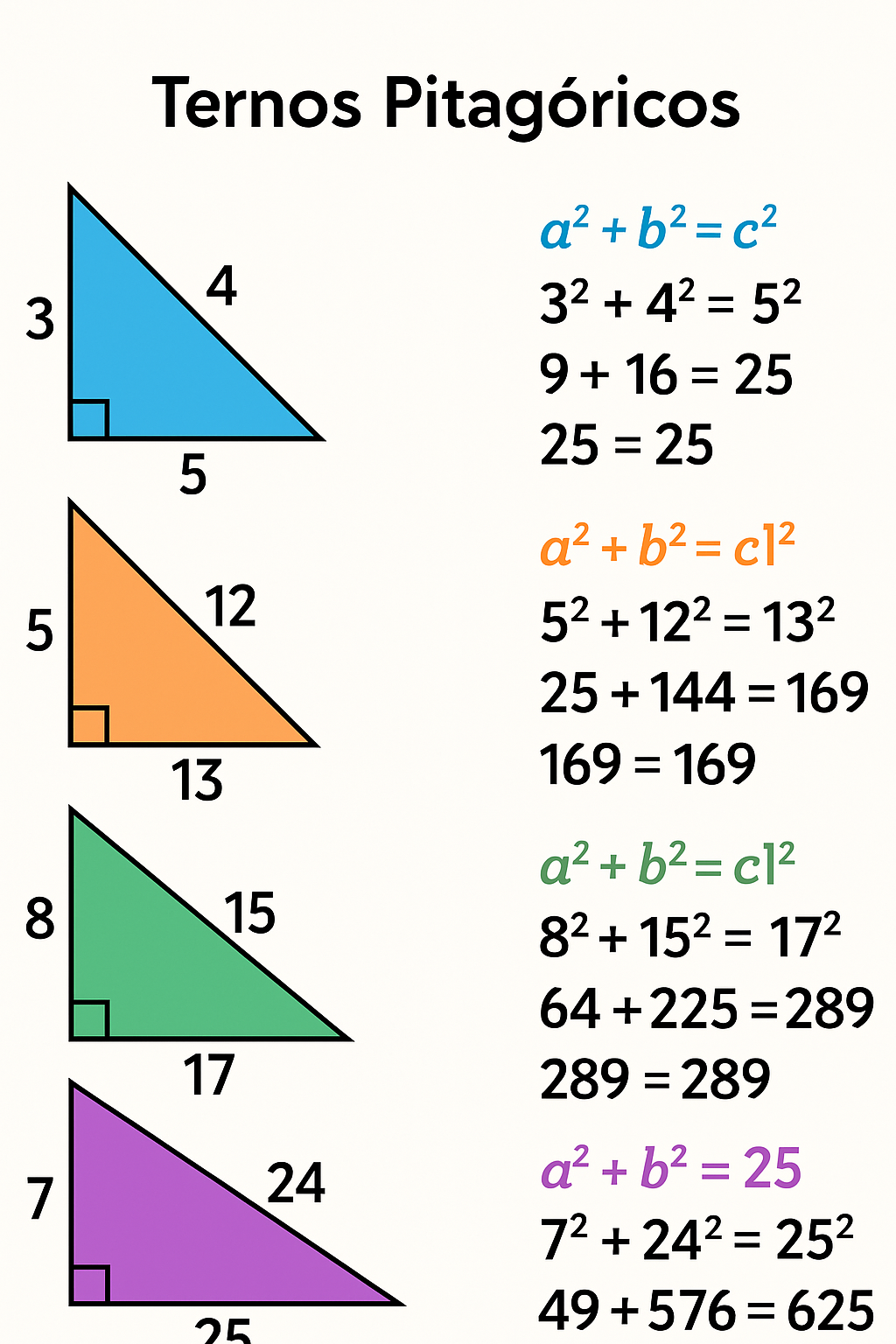
(3, 4, 5)
(5, 12, 13)
(8, 15, 17)
(7, 24, 25)
(9, 40, 41)
(11, 60, 61)
Uma propriedade interessante é que se multiplicarmos todos os números de um terno pitagórico pelo mesmo valor, obtemos outro terno pitagórico. Por exemplo, multiplicando (3, 4, 5) por 2, obtemos (6, 8, 10), que também é um terno pitagórico.
Existe uma fórmula para gerar ternos pitagóricos: para quaisquer números inteiros positivos m e n, com m > n, o terno (m^2 – n^2, 2mn, m^2 + n^2) é um terno pitagórico. Por exemplo, com m = 2 e n = 1, obtemos (3, 4, 5).
Aplicações Práticas do Teorema de Pitágoras no Cotidiano
O Teorema de Pitágoras não é apenas um conceito teórico; ele tem inúmeras aplicações práticas em nosso dia a dia:
Na Construção Civil e Arquitetura
Verificação de esquadro: Pedreiros e carpinteiros usam a relação 3-4-5 para garantir que cantos estejam em ângulo reto.
Cálculo de diagonais: Arquitetos usam o teorema para calcular diagonais de salas, terrenos e estruturas.
Projeto de escadas: O teorema ajuda a determinar a relação entre a altura, o comprimento horizontal e a inclinação de uma escada.
Na Navegação e Localização
Cálculo de distâncias: Navegadores usam o teorema para determinar a distância direta entre dois pontos.
Sistemas GPS: Os algoritmos de posicionamento global utilizam o teorema para calcular distâncias e posições.
Aviação: Pilotos usam o teorema para calcular rotas diretas entre aeroportos.
Na Física e Engenharia
Decomposição de forças: Engenheiros usam o teorema para analisar forças em diferentes direções.
Cálculo de velocidades: Físicos aplicam o teorema para determinar a velocidade resultante de movimentos em diferentes direções.
Design de estruturas: O teorema é fundamental no cálculo de tensões e forças em estruturas como pontes e edifícios.
Na Arte e Design
Perspectiva: Artistas usam o teorema para criar perspectivas realistas em desenhos e pinturas.
Design de produtos: Designers aplicam o teorema para calcular dimensões e proporções de objetos.
Fotografia: Fotógrafos usam o teorema para calcular distâncias focais e ângulos de visão.
Na Tecnologia
Processamento de imagens: Algoritmos de computador usam o teorema para transformações e rotações de imagens.
Jogos 3D: Programadores aplicam o teorema para calcular distâncias e colisões em ambientes virtuais.
Realidade virtual: O teorema é usado para calcular perspectivas e posicionamentos em ambientes imersivos.
Relação com Outros Conceitos Matemáticos
O Teorema de Pitágoras está intimamente relacionado com vários outros conceitos matemáticos importantes:
Trigonometria
O teorema é a base para a definição das funções trigonométricas seno, cosseno e tangente. Por exemplo, em um triângulo retângulo com hipotenusa c e catetos a e b:
sen(θ) = cateto oposto / hipotenusa = a/c
cos(θ) = cateto adjacente / hipotenusa = b/c
tan(θ) = cateto oposto / cateto adjacente = a/b
Geometria Analítica
A fórmula da distância entre dois pontos no plano cartesiano é uma aplicação direta do Teorema de Pitágoras: d = √[(x₂ – x₁)² + (y₂ – y₁)²]
Números Complexos
No plano complexo, o módulo de um número complexo z = a + bi é dado por |z| = √(a² + b²), que é essencialmente o Teorema de Pitágoras aplicado ao plano complexo.
Generalização para Espaços de Dimensões Superiores
O Teorema de Pitágoras pode ser generalizado para espaços de dimensões superiores. Por exemplo, em um espaço tridimensional, a distância entre dois pontos é: d = √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²]
Esta é uma extensão natural do teorema para três dimensões.
Dicas para Resolver Problemas com o Teorema de Pitágoras
Para aplicar o Teorema de Pitágoras com sucesso em problemas matemáticos, considere estas dicas:
Identificando Quando Usar o Teorema
O Teorema de Pitágoras deve ser usado quando:
O problema envolve um triângulo retângulo explícito
É possível identificar ou construir um triângulo retângulo na situação
O problema envolve distâncias perpendiculares ou diagonais
Há menção a ângulos retos ou perpendiculares
Erros Comuns a Evitar
Não verificar se o triângulo é retângulo: O teorema só se aplica a triângulos retângulos.
Confundir hipotenusa e catetos: A hipotenusa é sempre o lado oposto ao ângulo reto e é o lado mais longo.
Esquecer de extrair a raiz quadrada: Lembre-se que c² = a² + b² significa que c = √(a² + b²).
Aplicar o teorema em unidades diferentes: Certifique-se de que todas as medidas estão na mesma unidade antes de aplicar o teorema.
Estratégias de Verificação
Substituir os valores na equação: Após encontrar o valor desconhecido, substitua-o na equação original para verificar se a igualdade é satisfeita.
Verificar se o resultado faz sentido: Por exemplo, a hipotenusa deve ser maior que qualquer um dos catetos.
Usar aproximações: Em problemas com números irracionais, use aproximações para verificar se o resultado está na direção correta.
Conclusão: A Importância Atemporal do Teorema de Pitágoras
O Teorema de Pitágoras é um dos pilares fundamentais da matemática, com aplicações que transcendem o tempo e as culturas. Desde sua descoberta há mais de 2500 anos, ele continua sendo essencial em campos tão diversos quanto a arquitetura, a navegação, a física, a engenharia e a tecnologia moderna.
O que torna o Teorema de Pitágoras tão especial é sua combinação de simplicidade e profundidade. A equação c² = a² + b² é fácil de memorizar, mas suas implicações e aplicações são vastas e poderosas. Ele nos mostra como a matemática pode ser ao mesmo tempo elegante em sua formulação e prática em suas aplicações.
Ao dominar o Teorema de Pitágoras, você não está apenas aprendendo uma fórmula matemática, mas adquirindo uma ferramenta que permite resolver problemas reais e compreender melhor o mundo ao seu redor. É um conhecimento que transcende a sala de aula e encontra aplicações em praticamente todas as áreas que envolvem medidas, distâncias e geometria.
Agora que você compreende o Teorema de Pitágoras, suas origens, demonstrações, aplicações e como utilizá-lo, está pronto para resolver os exercícios a seguir e consolidar seu aprendizado.
Algumas video-aulas sobre o assunto:
http://www.youtube.com/watch?v=7YeYeL2MjB4
Canal: Dicasdemat Sandro Curió
http://www.youtube.com/watch?v=RxfPjqXx-g0
Canal: Gis com Giz Matemática
