Volumes Desvendados: Guia Completo para o Ensino Fundamental

Você já se perguntou como calcular a quantidade de água em uma piscina? Ou quanto ar cabe dentro de um balão? Ou ainda, como os engenheiros determinam a quantidade exata de concreto necessária para uma construção? A resposta para essas e muitas outras questões está no estudo dos Volumes, um dos conceitos mais importantes e práticos da geometria espacial.

Neste artigo, vamos explorar todos os aspectos desse tema fascinante, com explicações simples, exemplos práticos e imagens ilustrativas para facilitar seu entendimento. Prepare-se para descobrir como o cálculo de volumes está presente em nosso dia a dia e como ele pode ser aplicado para resolver problemas reais!

O que é Volume

O volume é a medida do espaço ocupado por um corpo ou objeto tridimensional. Em termos mais simples, é a quantidade de espaço que um sólido ocupa ou a quantidade de material que ele contém.

Imagine um aquário: o volume representa a quantidade de água que pode ser colocada dentro dele. Ou pense em uma caixa: o volume indica quanto espaço há disponível para armazenar objetos em seu interior.

Unidades de Medida de Volume

As unidades de medida de volume são derivadas das unidades de comprimento elevadas ao cubo. No Sistema Internacional de Unidades (SI), a unidade padrão de volume é o metro cúbico (m³), que corresponde ao espaço ocupado por um cubo com 1 metro de aresta.

Outras unidades comuns incluem:

• Centímetro cúbico (cm³): 1 m³ = 1.000.000 cm³

• Decímetro cúbico (dm³): 1 m³ = 1.000 dm³

• Milímetro cúbico (mm³): 1 m³ = 1.000.000.000 mm³

• Litro (L): 1 L = 1 dm³ = 1.000 cm³

• Mililitro (mL): 1 mL = 1 cm³

É importante notar que o litro, embora seja uma unidade de capacidade, é numericamente igual ao decímetro cúbico, o que estabelece uma relação direta entre volume e capacidade.

Representação Visual do Volume

Para visualizar o conceito de volume, podemos pensar em preencher um espaço tridimensional com cubos unitários. Por exemplo, um cubo com 3 cm de aresta pode ser preenchido com 27 cubos de 1 cm de aresta (3 × 3 × 3 = 27). Isso nos dá um volume de 27 cm³.

Esta representação nos ajuda a entender que o volume é uma medida tridimensional, diferente da área (bidimensional) ou do comprimento (unidimensional).

Princípio de Cavalieri

O Princípio de Cavalieri, formulado pelo matemático italiano Bonaventura Cavalieri no século XVII, é uma ferramenta poderosa para o cálculo de volumes. Ele estabelece que:

"Se dois sólidos têm a mesma altura e se as seções feitas por planos paralelos às bases e à mesma distância delas têm áreas iguais, então os volumes dos sólidos são iguais."

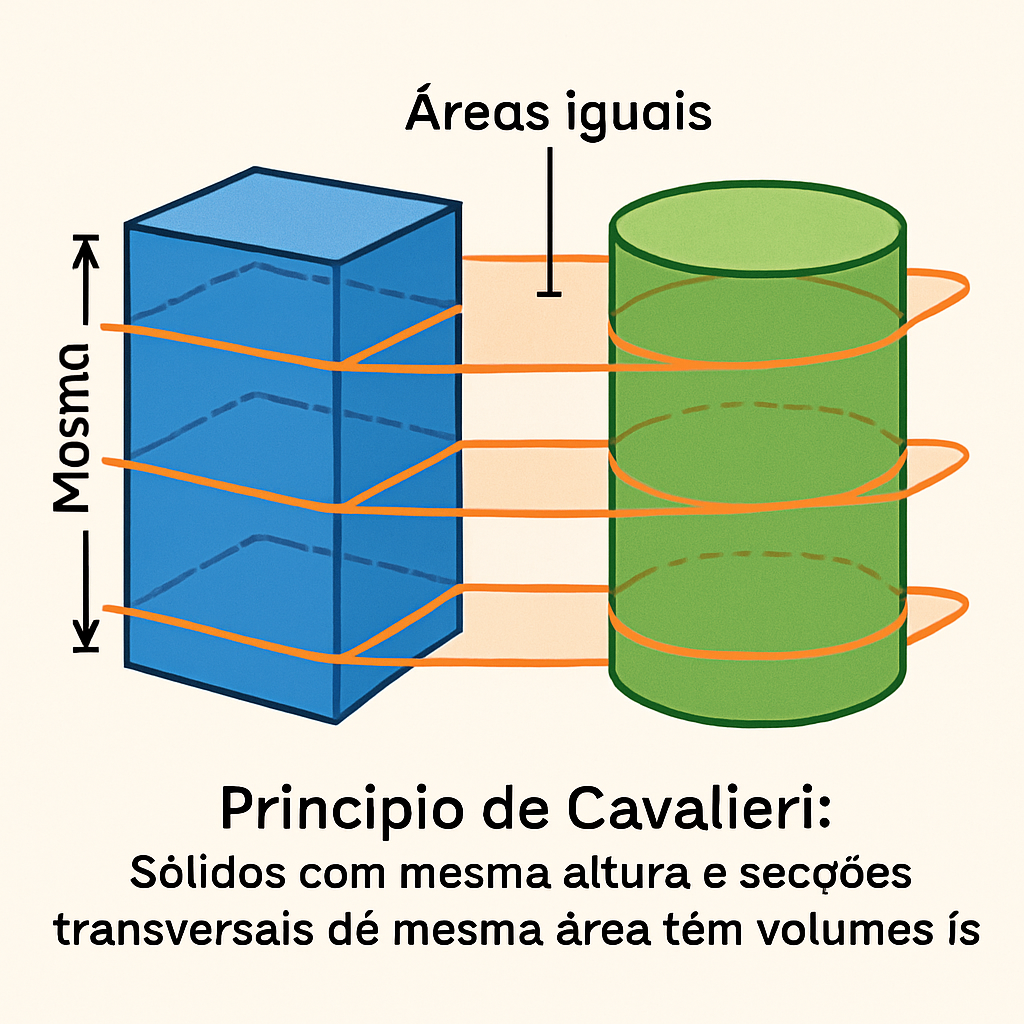
Em termos mais simples, se cortarmos dois sólidos com planos paralelos às suas bases e, em cada altura, as áreas das seções forem iguais, então os volumes dos sólidos também serão iguais, independentemente de suas formas.

Este princípio nos permite calcular volumes de sólidos complexos comparando-os com sólidos mais simples cujos volumes já conhecemos. Por exemplo, podemos usar o Princípio de Cavalieri para demonstrar que o volume de uma pirâmide é um terço do volume de um prisma com a mesma base e altura.

Volume do Paralelepípedo

O paralelepípedo é um sólido geométrico formado por seis faces, todas paralelogramos. Quando todas as faces são retângulos, temos um caso especial chamado paralelepípedo retângulo.

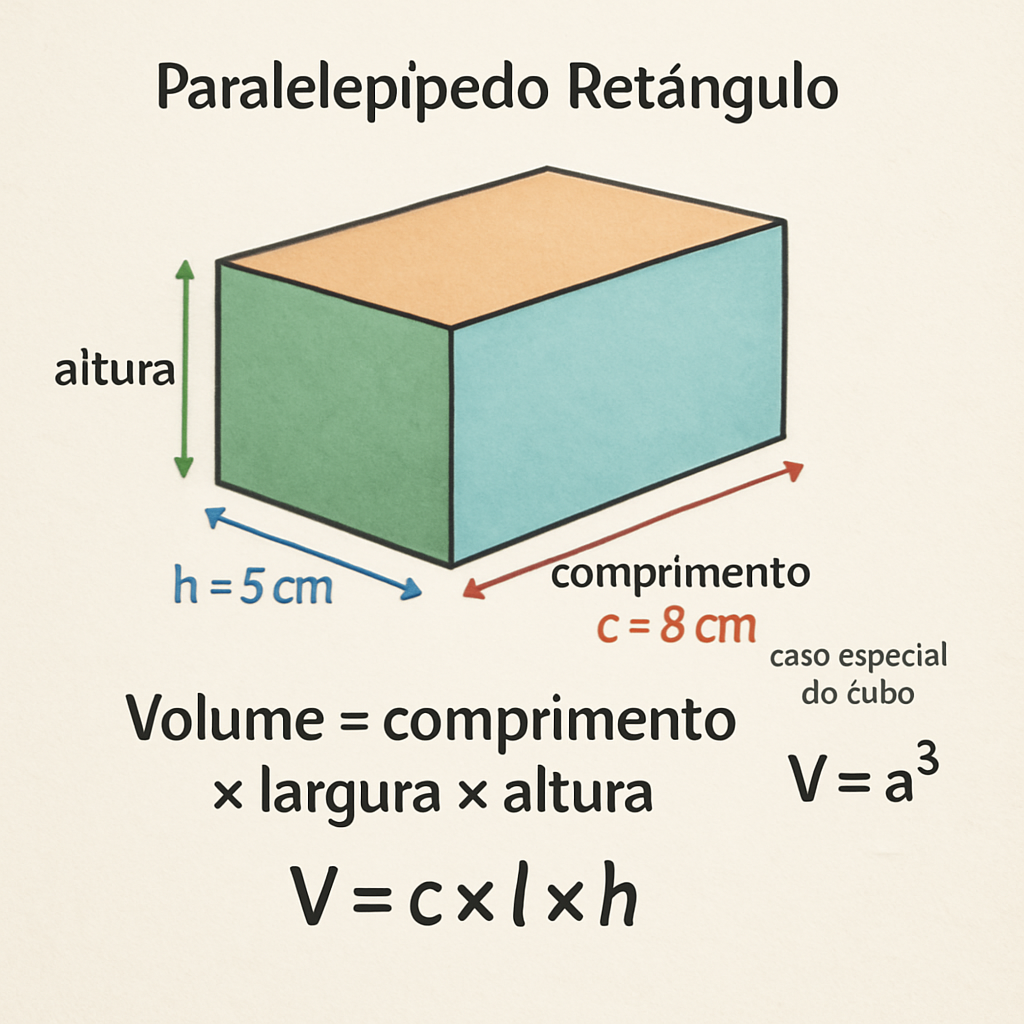
O volume de um paralelepípedo retângulo é calculado multiplicando-se suas três dimensões: comprimento, largura e altura.

V = c × l × h

Onde:

• V é o volume

• c é o comprimento

• l é a largura

• h é a altura

Caso Especial: O Cubo

O cubo é um caso particular do paralelepípedo, onde todas as arestas têm o mesmo comprimento. Seu volume é calculado elevando-se a medida da aresta ao cubo:

V = a³

Onde:

• V é o volume

• a é a medida da aresta

Exemplo: Um cubo com aresta de 5 cm tem volume V = 5³ = 125 cm³.

Volume do Prisma

Um prisma é um sólido geométrico que possui duas faces paralelas e congruentes, chamadas bases, e faces laterais que são paralelogramos. Os prismas são classificados de acordo com o polígono que forma suas bases: prisma triangular, quadrangular, pentagonal, hexagonal, etc.

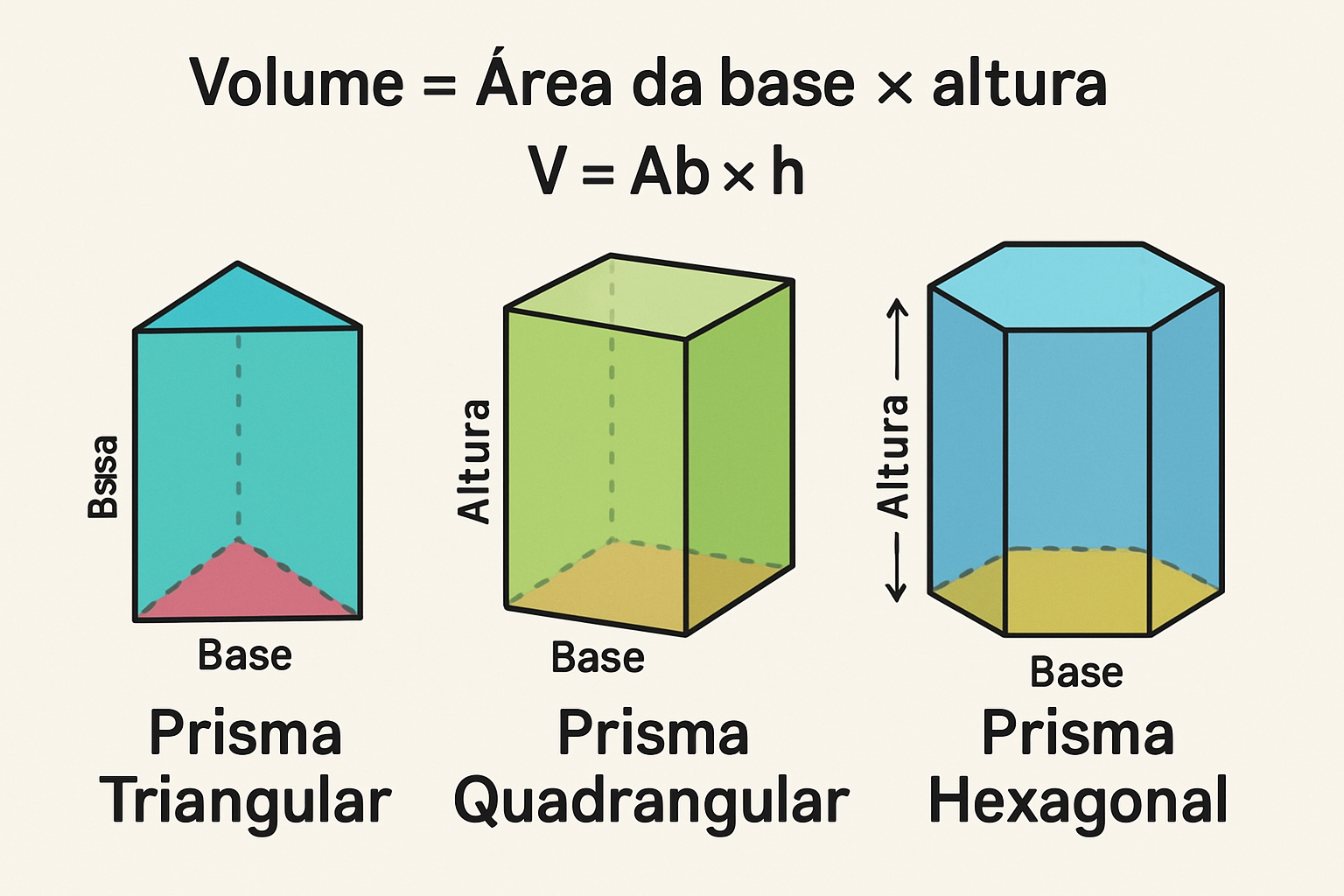
O volume de qualquer prisma é calculado multiplicando-se a área da base pela altura:

V = A_base × h

Onde:

• V é o volume

• A_base é a área da base

• h é a altura (distância entre as bases)

Exemplo: Um prisma triangular com base de área 12 cm² e altura 7 cm tem volume V = 12 × 7 = 84 cm³.

Esta fórmula é válida para qualquer tipo de prisma, independentemente da forma de sua base. O importante é calcular corretamente a área da base e multiplicá-la pela altura.

Volume da Pirâmide

Uma pirâmide é um sólido geométrico formado por uma base poligonal e faces laterais triangulares que se encontram em um ponto chamado vértice ou ápice. Assim como os prismas, as pirâmides são classificadas de acordo com o polígono que forma sua base: pirâmide triangular, quadrangular, pentagonal, etc.

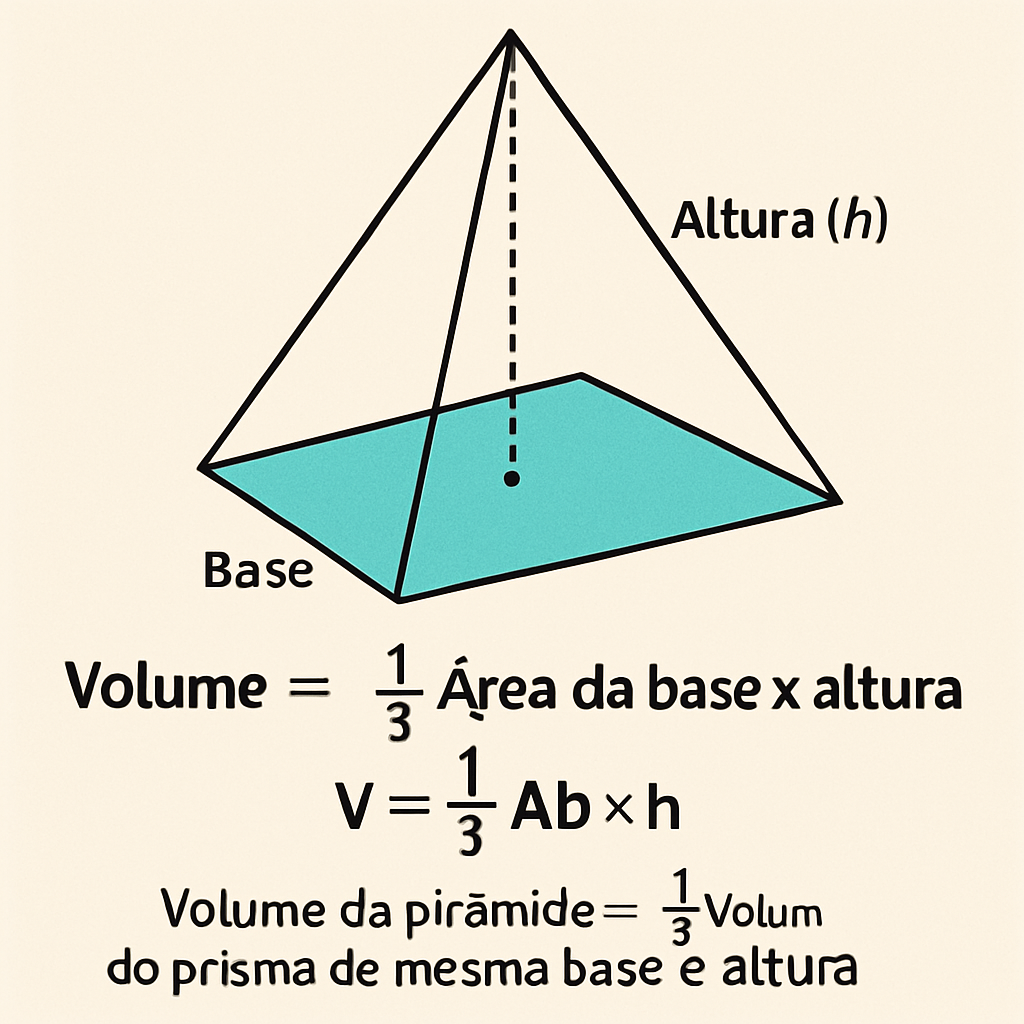
O volume de uma pirâmide é calculado usando a seguinte fórmula:

V = (1/3) × A_base × h

Onde:

• V é o volume

• A_base é a área da base

• h é a altura (distância perpendicular do vértice à base)

Exemplo: Uma pirâmide quadrangular com base de área 36 cm² e altura 9 cm tem volume V = (1/3) × 36 × 9 = 108 cm³.

É interessante notar que o volume de uma pirâmide é exatamente um terço do volume de um prisma com a mesma base e altura. Esta relação pode ser demonstrada usando o Princípio de Cavalieri.

Volume do Cilindro

O cilindro é um sólido geométrico formado por duas bases circulares paralelas e congruentes, e uma superfície lateral curva. Pode ser visto como um prisma com bases circulares.

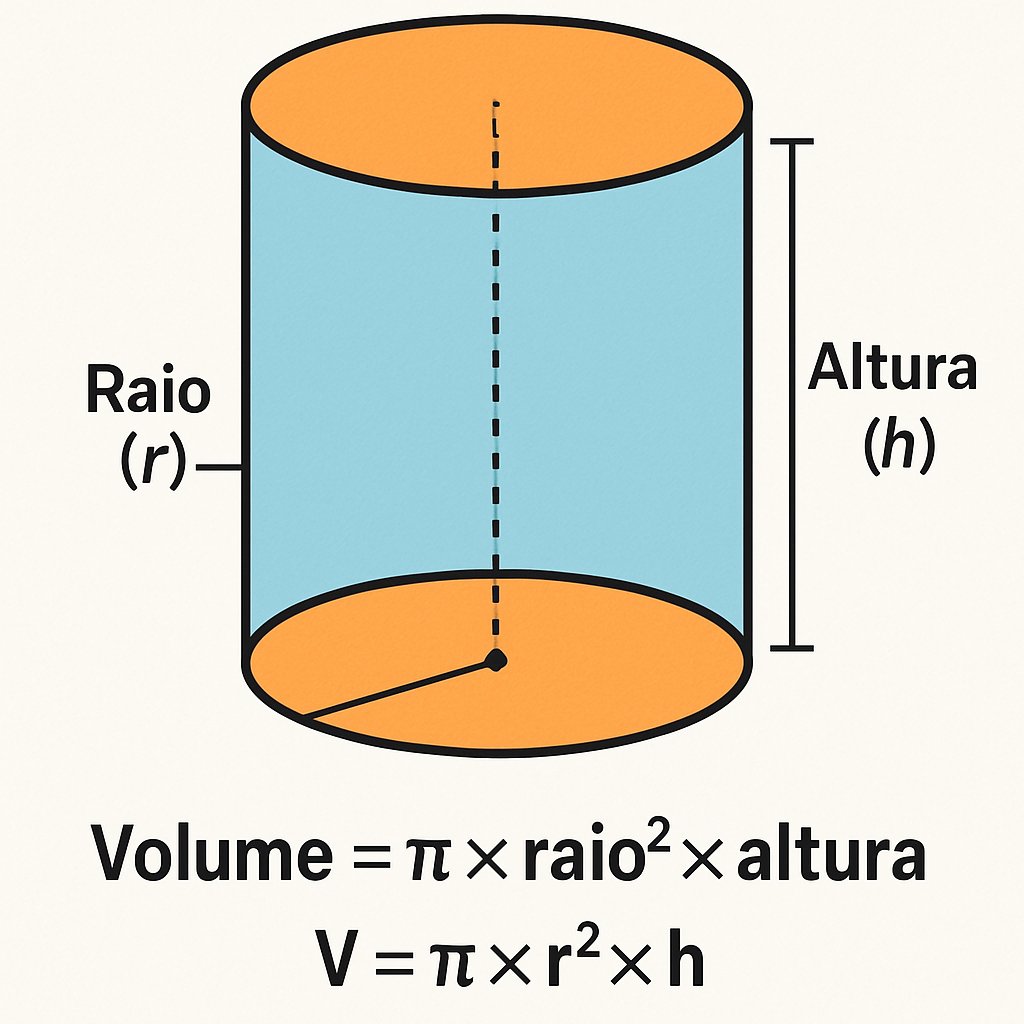
O volume de um cilindro é calculado multiplicando-se a área da base circular pela altura:

V = π × r² × h

Onde:

• V é o volume

• π (pi) é aproximadamente 3,14159...

• r é o raio da base

• h é a altura (distância entre as bases)

Exemplo: Um cilindro com raio da base de 4 cm e altura 10 cm tem volume V = π × 4² × 10 = π × 16 × 10 = 160π ≈ 502,4 cm³.

O cilindro é um sólido muito comum no dia a dia, presente em objetos como latas de refrigerante, rolos de papel, tubos, etc.

Volume do Cone

O cone é um sólido geométrico formado por uma base circular e uma superfície lateral curva que se afunila até um ponto chamado vértice ou ápice. Pode ser visto como uma pirâmide com base circular.

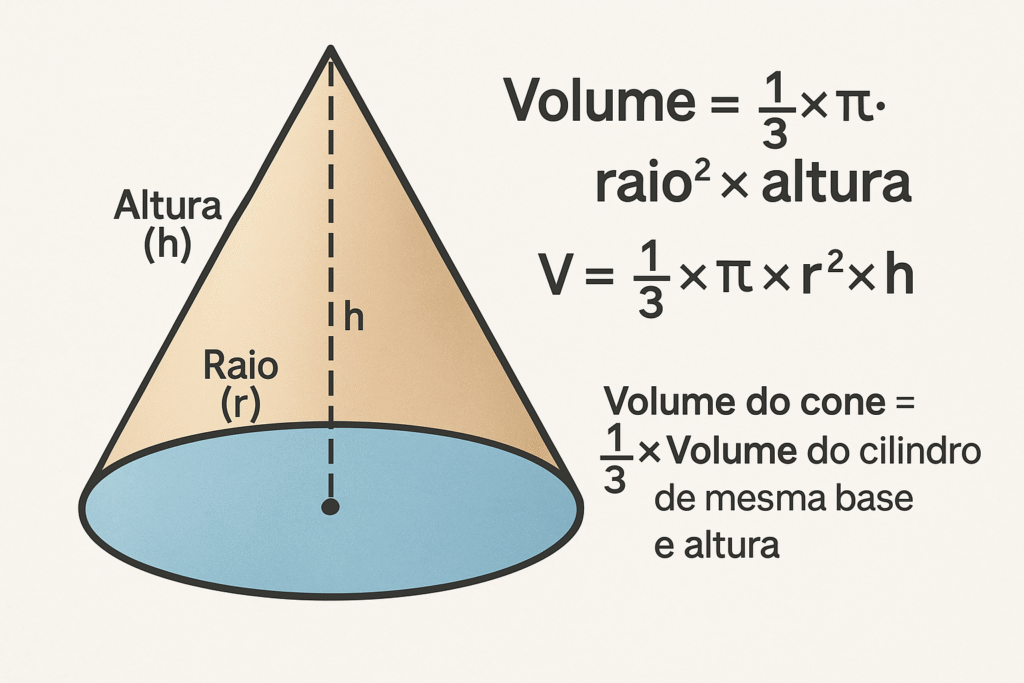
O volume de um cone é calculado usando a seguinte fórmula:

V = (1/3) × π × r² × h

Onde:

• V é o volume

• π (pi) é aproximadamente 3,14159...

• r é o raio da base

• h é a altura (distância perpendicular do vértice à base)

Exemplo: Um cone com raio da base de 5 cm e altura 12 cm tem volume V = (1/3) × π × 5² × 12 = (1/3) × π × 25 × 12 = 100π ≈ 314 cm³.

Assim como a pirâmide em relação ao prisma, o volume de um cone é exatamente um terço do volume de um cilindro com a mesma base e altura.

Volume da Esfera

A esfera é um sólido geométrico formado por todos os pontos do espaço que estão a uma mesma distância (raio) de um ponto fixo (centro). É o equivalente tridimensional de um círculo.

O volume de uma esfera é calculado usando a seguinte fórmula:

V = (4/3) × π × r³

Onde:

• V é o volume

• π (pi) é aproximadamente 3,14159...

• r é o raio da esfera

Exemplo: Uma esfera com raio de 6 cm tem volume V = (4/3) × π × 6³ = (4/3) × π × 216 = 288π ≈ 904,32 cm³.

A fórmula do volume da esfera foi descoberta por Arquimedes no século III a.C., o que foi uma conquista notável para a época, considerando as limitações dos métodos matemáticos disponíveis.

Relações entre Volumes de Sólidos

Existem várias relações interessantes entre os volumes de diferentes sólidos geométricos. Conhecer essas relações pode facilitar a resolução de problemas e proporcionar uma compreensão mais profunda da geometria espacial.

Relação entre Prisma e Pirâmide

Como mencionado anteriormente, o volume de uma pirâmide é um terço do volume de um prisma com a mesma base e altura:

V_pirâmide = (1/3) × V_prisma

Relação entre Cilindro e Cone

De forma similar, o volume de um cone é um terço do volume de um cilindro com a mesma base e altura:

V_cone = (1/3) × V_cilindro

Relação entre Cilindro e Esfera

Se considerarmos um cilindro circunscrito a uma esfera (ou seja, um cilindro que "envolve" perfeitamente a esfera), com altura igual ao diâmetro da esfera, a relação entre seus volumes é:

V_esfera = (2/3) × V_cilindro

Esta é uma relação descoberta por Arquimedes e é fundamental para a demonstração da fórmula do volume da esfera.

Relação entre Cubo e Esfera Inscrita

Se uma esfera está inscrita em um cubo (ou seja, a esfera toca o cubo em seus seis pontos médios das faces), a relação entre seus volumes é:

V_esfera = (π/6) × V_cubo ≈ 0,5236 × V_cubo

Isso significa que a esfera ocupa aproximadamente 52,36% do volume do cubo.

Estas relações não apenas são matematicamente elegantes, mas também têm aplicações práticas em diversos campos, como engenharia, arquitetura e design.

Aplicações Práticas do Cálculo de Volumes

O cálculo de volumes tem inúmeras aplicações práticas em nosso dia a dia e em diversas áreas profissionais:

Na Construção Civil

• Cálculo de materiais: Engenheiros e arquitetos usam o cálculo de volumes para determinar a quantidade de concreto, areia, brita e outros materiais necessários para uma construção.

• Dimensionamento de reservatórios: O volume é essencial para projetar caixas d'água, cisternas e outros sistemas de armazenamento.

• Movimentação de terra: Em obras que envolvem escavações, o cálculo do volume de terra a ser removido é fundamental para o planejamento e orçamento.

Na Indústria

• Design de embalagens: Fabricantes usam o cálculo de volumes para otimizar o design de embalagens, reduzindo custos e desperdício de material.

• Tanques e recipientes: Indústrias químicas, alimentícias e farmacêuticas precisam calcular volumes com precisão para processos de produção e armazenamento.

• Transporte de cargas: O volume é um fator crucial no planejamento logístico e no cálculo de custos de transporte.

No Cotidiano

• Cozinha: Receitas frequentemente especificam volumes de ingredientes (xícaras, colheres, litros).

• Consumo de água: O cálculo do volume ajuda a estimar o consumo de água em atividades como encher uma piscina ou regar um jardim.

• Armazenamento doméstico: Ao organizar objetos em caixas ou armários, consideramos implicitamente o volume disponível e necessário.

Na Ciência

• Medicina: O volume é usado para calcular dosagens de medicamentos, capacidade pulmonar e volume sanguíneo.

• Meteorologia: O cálculo de volumes de massas de ar é importante para previsões climáticas.

• Geologia: Geólogos estimam volumes de formações rochosas, reservatórios de petróleo e depósitos minerais.

Estas aplicações demonstram como o conhecimento sobre volumes transcende a sala de aula e tem impacto direto em diversos aspectos de nossas vidas.

Como Resolver Problemas de Volume

Para resolver problemas envolvendo volumes, podemos seguir uma abordagem sistemática:

1. Identificar o Sólido Geométrico

O primeiro passo é identificar qual sólido geométrico está envolvido no problema. Isso determinará qual fórmula de volume deve ser utilizada.

2. Identificar os Dados Fornecidos

Verifique quais informações são fornecidas no problema: dimensões, áreas, outros volumes relacionados, etc.

3. Escolher a Fórmula Adequada

Selecione a fórmula de volume apropriada para o sólido identificado:

• Paralelepípedo: V = c × l × h

• Cubo: V = a³

• Prisma: V = A_base × h

• Pirâmide: V = (1/3) × A_base × h

• Cilindro: V = π × r² × h

• Cone: V = (1/3) × π × r² × h

• Esfera: V = (4/3) × π × r³

4. Substituir os Valores e Calcular

Substitua os valores conhecidos na fórmula e realize os cálculos necessários. Lembre-se de verificar se todas as unidades estão consistentes.

5. Verificar a Unidade de Medida

O resultado do cálculo de volume deve ser expresso em unidades cúbicas (m³, cm³, etc.) ou em unidades de capacidade (L, mL, etc.).

6. Interpretar o Resultado

Analise se o resultado obtido faz sentido no contexto do problema. Um volume negativo ou excessivamente grande/pequeno pode indicar um erro de cálculo.

Dicas Adicionais

• Conversão de unidades: Muitas vezes é necessário converter entre diferentes unidades de volume. Lembre-se das relações: 1 m³ = 1.000 L, 1 L = 1.000 mL = 1.000 cm³.

• Decomposição: Para sólidos complexos, considere decompô-los em sólidos mais simples, calcular o volume de cada parte e depois somá-los.

• Princípio de Cavalieri: Em alguns casos, pode ser útil aplicar o Princípio de Cavalieri para comparar o volume desconhecido com um volume conhecido.

Seguindo estes passos e dicas, você estará bem equipado para resolver uma ampla variedade de problemas envolvendo volumes.

Conclusão: A Importância do Estudo de Volumes

O estudo dos volumes é uma parte fundamental da geometria espacial, com aplicações que vão muito além da sala de aula. Desde a antiguidade, quando Arquimedes descobriu como calcular o volume de uma esfera, até os dias atuais, com simulações computacionais de fluidos em três dimensões, o conceito de volume tem sido essencial para o avanço da ciência e da tecnologia.

Compreender como calcular o volume de diferentes sólidos geométricos nos permite:

• Resolver problemas práticos do cotidiano

• Tomar decisões mais informadas em projetos de engenharia e arquitetura

• Entender melhor o mundo tridimensional em que vivemos

• Desenvolver o raciocínio espacial e a capacidade de visualização

As fórmulas que aprendemos neste artigo – para paralelepípedos, prismas, pirâmides, cilindros, cones e esferas – são ferramentas poderosas que nos permitem quantificar e comparar o espaço ocupado por diferentes objetos e estruturas.

Ao dominar o cálculo de volumes, você adquire uma habilidade matemática que tem aplicações práticas imediatas e que serve como base para estudos mais avançados em áreas como cálculo integral, física e engenharia.

Agora que você compreende os princípios fundamentais do cálculo de volumes, está pronto para praticar com os exercícios a seguir e consolidar seu aprendizado.

Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=3iWl-Liuw5s

Canal:Descomplica

http://www.youtube.com/watch?v=TN2zv_vSH70

Canal: Gis com Giz Matemática