Desvendando os Ângulos: Trigonometria no Triângulo Retângulo para Iniciantes!

Introdução: Além dos Lados, Explorando os Ângulos!

Se você já explorou o fascinante Teorema de Pitágoras, sabe que ele nos revela uma relação poderosa entre os lados de um triângulo retângulo. Mas e os ângulos? Como eles se relacionam com as medidas dos lados? É aqui que entra em cena a Trigonometria, um ramo da matemática que constrói pontes entre os ângulos e os lados dos triângulos, especialmente do triângulo retângulo.

A palavra "Trigonometria" vem do grego: "trigonon" (triângulo) e "metron" (medida). Essencialmente, ela nos ensina a medir triângulos, não apenas seus lados, mas também seus ângulos e as relações intrínsecas entre eles. Pode parecer algo complexo à primeira vista, mas a trigonometria no triângulo retângulo se baseia em ideias bastante intuitivas e extremamente úteis.

Desde os tempos antigos, a trigonometria tem sido uma ferramenta indispensável. Navegadores a usavam para traçar rotas pelos vastos oceanos, astrônomos para medir distâncias celestiais, engenheiros para projetar estruturas seguras e até mesmo artistas e desenvolvedores de jogos a utilizam hoje para criar perspectivas realistas e movimentos precisos. Ela está presente no cálculo da altura de uma montanha inacessível, na determinação da largura de um rio, na inclinação de uma rampa e em muitas outras situações práticas.

Neste guia completo, vamos mergulhar no mundo da Trigonometria no Triângulo Retângulo. Nosso objetivo é desmistificar as famosas razões trigonométricas – Seno, Cosseno e Tangente – explicando seus conceitos de forma clara, simples e acessível, especialmente para quem está começando a explorar esse tema no ensino fundamental. Prepare-se para descobrir como os ângulos e os lados de um triângulo retângulo conversam entre si e como você pode usar essa conversa para resolver problemas intrigantes! Vamos juntos desvendar os segredos das Razões Trigonométricas.

1. Relembrando o Triângulo Retângulo: A Base de Tudo

Antes de entrarmos nas razões trigonométricas, é fundamental estarmos confortáveis com o protagonista da nossa história: o triângulo retângulo. Vamos relembrar suas características principais:

• Definição: Um triângulo retângulo é qualquer triângulo que possui um ângulo reto, ou seja, um ângulo que mede exatamente 90° (noventa graus). Esse ângulo é geralmente marcado com um pequeno quadrado no vértice.

• Elementos Essenciais:

  • Hipotenusa: É o lado oposto ao ângulo reto. É sempre o lado mais longo do triângulo retângulo.

  • Catetos: São os dois lados que formam o ângulo reto. Eles são menores que a hipotenusa.

• Ângulos Agudos: Além do ângulo reto (90°), um triângulo retângulo possui dois ângulos agudos (menores que 90°). Uma propriedade importante é que a soma dos ângulos internos de qualquer triângulo é sempre 180°. Portanto, em um triângulo retângulo, a soma dos dois ângulos agudos é sempre 90° (eles são complementares).

Identificando Catetos em Relação a um Ângulo Agudo:

Essa parte é crucial para a trigonometria! A classificação de um cateto como "oposto" ou "adjacente" depende do ângulo agudo que estamos analisando.

Imagine que estamos focando em um dos ângulos agudos, que chamaremos de α (alfa):

• Cateto Oposto (CO): É o cateto que está do outro lado do triângulo, diretamente em frente ao ângulo α. Ele não toca o vértice do ângulo α (exceto pela hipotenusa).

• Cateto Adjacente (CA): É o cateto que está ao lado do ângulo α, formando um dos lados desse ângulo (o outro lado é a hipotenusa). A palavra "adjacente" significa "ao lado".

Se mudarmos o foco para o outro ângulo agudo, β (beta), a classificação dos catetos se inverte:

• O cateto que era oposto a α se torna adjacente a β.

• O cateto que era adjacente a α se torna oposto a β.

A hipotenusa é sempre a mesma, independentemente do ângulo agudo escolhido.

Dominar a identificação correta da hipotenusa, do cateto oposto e do cateto adjacente para um ângulo agudo específico é o primeiro passo indispensável para aplicar as razões trigonométricas.

2. As Razões Trigonométricas: Seno, Cosseno e Tangente

A grande ideia da trigonometria no triângulo retângulo é que existe uma relação constante entre as medidas dos lados e as medidas dos ângulos agudos. Imagine vários triângulos retângulos que são semelhantes entre si (possuem os mesmos ângulos agudos, mas tamanhos diferentes). Se pegarmos um ângulo agudo específico, por exemplo, 30°, em todos esses triângulos, a razão (divisão) entre o cateto oposto a ele e a hipotenusa será sempre a mesma, não importa o tamanho do triângulo! O mesmo vale para outras razões entre os lados.

Essas razões constantes recebem nomes especiais e são a base da trigonometria: Seno, Cosseno e Tangente.

Para um ângulo agudo α em um triângulo retângulo, definimos:

• Seno de α (abreviado como sen α): É a razão entre a medida do Cateto Oposto a α e a medida da Hipotenusa. sen α = Cateto Oposto / Hipotenusa = CO / H

• Cosseno de α (abreviado como cos α): É a razão entre a medida do Cateto Adjacente a α e a medida da Hipotenusa. cos α = Cateto Adjacente / Hipotenusa = CA / H

• Tangente de α (abreviada como tan α ou tg α): É a razão entre a medida do Cateto Oposto a α e a medida do Cateto Adjacente a α. tan α = Cateto Oposto / Cateto Adjacente = CO / CA

Mnemônico para Lembrar:

Uma forma popular de memorizar essas definições é usar a sigla SOH CAH TOA (pronuncia-se "so-ca-toa"):

• SOH: Seno = Oposto / Hipotenusa

• CAH: Cosseno = Adjacente / Hipotenusa

• TOA: Tangente = Oposto / Adjacente

Existem outras frases mnemônicas em português, como "Socorro! O Homem Caiu Aqui Hoje Tomando Outra Cerveja Azul" (S=O/H, C=A/H, T=O/A), ou variações que podem ajudar a fixar as fórmulas.

Exemplo Numérico:

Considere um triângulo retângulo famoso, cujos lados medem 3, 4 e 5 unidades (o triângulo pitagórico 3-4-5). A hipotenusa é o maior lado, H = 5. Os catetos são 3 e 4.

Vamos chamar de α o ângulo oposto ao lado de medida 3, e de β o ângulo oposto ao lado de medida 4.

• Para o ângulo α:

  • Cateto Oposto (CO) = 3

  • Cateto Adjacente (CA) = 4

  • Hipotenusa (H) = 5

  • sen α = CO / H = 3 / 5 = 0,6

  • cos α = CA / H = 4 / 5 = 0,8

  • tan α = CO / CA = 3 / 4 = 0,75

• Para o ângulo β:

  • Cateto Oposto (CO) = 4

  • Cateto Adjacente (CA) = 3

  • Hipotenusa (H) = 5

  • sen β = CO / H = 4 / 5 = 0,8

  • cos β = CA / H = 3 / 5 = 0,6

  • tan β = CO / CA = 4 / 3 ≈ 1,33

Note que sen α = cos β e cos α = sen β. Isso não é coincidência, como veremos a seguir!

Compreender e saber aplicar essas três razões fundamentais é a chave para resolver a maioria dos problemas de trigonometria no triângulo retângulo.

3. Relações Fundamentais: Conectando as Razões

As razões trigonométricas não são independentes; elas se relacionam entre si de maneiras importantes. Conhecer essas relações pode simplificar muitos cálculos e ajudar a resolver problemas onde nem todas as informações são dadas diretamente.

• Relação Fundamental da Trigonometria: A relação mais importante é: sen²(α) + cos²(α) = 1 Isso significa que, para qualquer ângulo agudo α, a soma do quadrado do seu seno com o quadrado do seu cosseno é sempre igual a 1.

  Demonstração Simples: Em um triângulo retângulo com ângulo α, cateto oposto CO, cateto adjacente CA e hipotenusa H: sen α = CO / H → sen²(α) = (CO)² / H² cos α = CA / H → cos²(α) = (CA)² / H² Somando: sen²(α) + cos²(α) = [(CO)² / H²] + [(CA)² / H²] = [(CO)² + (CA)²] / H² Pelo Teorema de Pitágoras, sabemos que (CO)² + (CA)² = H². Substituindo: sen²(α) + cos²(α) = H² / H² = 1.

• Relação da Tangente: A tangente de um ângulo pode ser expressa em termos do seno e do cosseno desse mesmo ângulo: tan(α) = sen(α) / cos(α)

  Demonstração Simples: sen(α) / cos(α) = (CO / H) / (CA / H) Dividir frações é o mesmo que multiplicar pela inversa da segunda: (CO / H) * (H / CA) Simplificando o H: CO / CA Mas CO / CA é a definição da tan(α). Portanto, tan(α) = sen(α) / cos(α).

• Relações entre Ângulos Complementares: Se α e β são os dois ângulos agudos de um triângulo retângulo, sabemos que α + β = 90° (são complementares). Como vimos no exemplo do triângulo 3-4-5:

  • O seno de um ângulo agudo é igual ao cosseno do seu complemento: sen(α) = cos(β) ou sen(α) = cos(90° - α).

  • O cosseno de um ângulo agudo é igual ao seno do seu complemento: cos(α) = sen(β) ou cos(α) = sen(90° - α).

  Isso acontece porque o cateto oposto a α é o cateto adjacente a β, e vice-versa.

Importância: Essas relações são ferramentas poderosas. Se você conhece o seno de um ângulo, pode encontrar o cosseno usando a Relação Fundamental. Se conhece o seno e o cosseno, pode encontrar a tangente. Se conhece o seno de 30°, sabe automaticamente o cosseno de 60°.

4. Ângulos Notáveis: 30°, 45° e 60°

Existem três ângulos agudos que aparecem com muita frequência em problemas de matemática e física: 30°, 45° e 60°. Por causa disso, e porque seus valores de seno, cosseno e tangente podem ser calculados exatamente usando geometria básica (sem precisar de calculadora), eles são chamados de ângulos notáveis.

É muito útil conhecer e memorizar os valores das razões trigonométricas para esses ângulos.

Dedução para 45°:

• Considere um quadrado de lado 1. Seus ângulos são todos 90°.

• Trace uma diagonal. Ela divide o quadrado em dois triângulos retângulos idênticos.

• Cada triângulo retângulo tem catetos de medida 1.

• Pelo Teorema de Pitágoras, a hipotenusa (a diagonal) mede: H² = 1² + 1² = 2 → H = √2.

• Os ângulos agudos desse triângulo são ambos de 45° (pois a diagonal divide o ângulo de 90° do quadrado ao meio).

• Agora, calculamos as razões para o ângulo de 45°:

  • sen 45° = CO / H = 1 / √2 = (1 √2) / (√2 √2) = √2 / 2

  • cos 45° = CA / H = 1 / √2 = √2 / 2

  • tan 45° = CO / CA = 1 / 1 = 1

Dedução para 30° e 60°:

• Considere um triângulo equilátero (todos os lados iguais, todos os ângulos iguais a 60°) de lado 2.

• Trace a altura relativa a uma das bases. A altura divide o triângulo equilátero em dois triângulos retângulos idênticos.

• Cada triângulo retângulo tem:

  • Hipotenusa = lado do triângulo equilátero = 2.

  • Um cateto = metade da base do triângulo equilátero = 2 / 2 = 1.

  • O outro cateto = altura (h). Por Pitágoras: 2² = 1² + h² → 4 = 1 + h² → h² = 3 → h = √3.

  • Os ângulos agudos desse triângulo retângulo são 30° (metade do ângulo de 60° do vértice superior) e 60° (o ângulo da base).

• Agora, calculamos as razões:

  • Para o ângulo de 30°: CO = 1, CA = √3, H = 2

    • sen 30° = CO / H = 1 / 2

    • cos 30° = CA / H = √3 / 2

    • tan 30° = CO / CA = 1 / √3 = (1 √3) / (√3 √3) = √3 / 3

  • Para o ângulo de 60°: CO = √3, CA = 1, H = 2

    • sen 60° = CO / H = √3 / 2

    • cos 60° = CA / H = 1 / 2

    • tan 60° = CO / CA = √3 / 1 = √3

Tabela dos Ângulos Notáveis:

É muito comum organizar esses valores em uma tabela para facilitar a consulta e memorização:

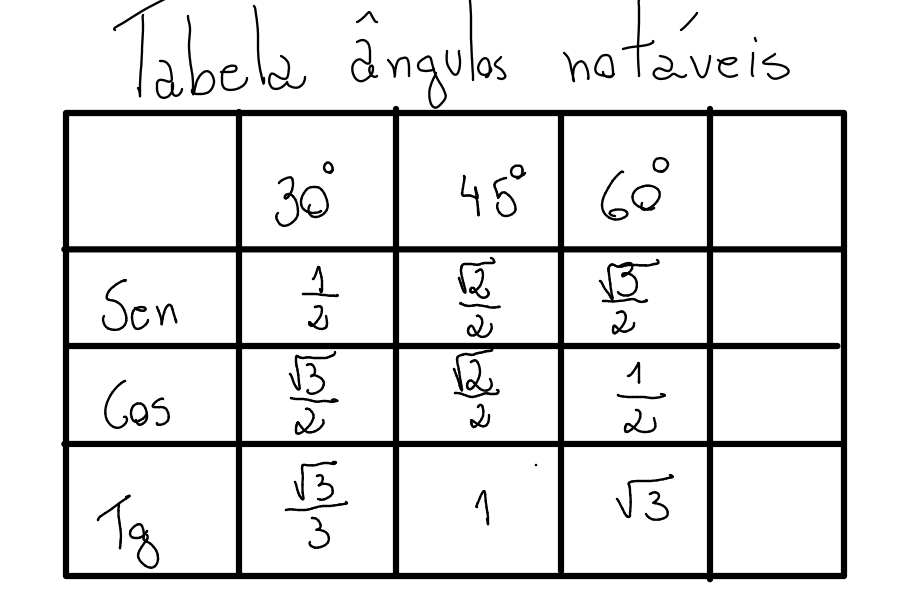
Dica de Memorização: Existe uma música ou padrão para lembrar: "1, 2, 3... 3, 2, 1... Tudo sobre 2... A raiz vai no 3 e no 2... A tangente é diferente, vejam só vocês: Raiz de 3 sobre 3, 1, Raiz de 3".

Conhecer esses valores de cor agiliza muito a resolução de exercícios!

5. Resolvendo Triângulos Retângulos: O Poder da Trigonometria

Um dos principais objetivos da trigonometria é "resolver" triângulos. Resolver um triângulo retângulo significa determinar as medidas de todos os seus três lados e de seus três ângulos, a partir de algumas informações conhecidas.

Com o Teorema de Pitágoras e as razões trigonométricas (seno, cosseno, tangente), podemos resolver praticamente qualquer triângulo retângulo se tivermos informações suficientes. Geralmente, precisamos conhecer pelo menos duas medidas, sendo pelo menos uma delas um lado.

Casos Comuns:

1. Conhecemos um ângulo agudo (α) e a medida de um lado:

   • Se conhecemos a Hipotenusa (H):

     • Para achar o Cateto Oposto (CO): Use sen α = CO / H → CO = H * sen α

     • Para achar o Cateto Adjacente (CA): Use cos α = CA / H → CA = H * cos α

   • Se conhecemos o Cateto Oposto (CO) ao ângulo α:

     • Para achar a Hipotenusa (H): Use sen α = CO / H → H = CO / sen α

     • Para achar o Cateto Adjacente (CA): Use tan α = CO / CA → CA = CO / tan α

   • Se conhecemos o Cateto Adjacente (CA) ao ângulo α:

     • Para achar a Hipotenusa (H): Use cos α = CA / H → H = CA / cos α

     • Para achar o Cateto Oposto (CO): Use tan α = CO / CA → CO = CA * tan α

   • O outro ângulo agudo (β) é fácil: β = 90° - α.

2. Conhecemos as medidas de dois lados:

   • Para achar o terceiro lado: Use o Teorema de Pitágoras (H² = (CO)² + (CA)²).

   • Para achar um dos ângulos agudos (α): Escolha uma razão trigonométrica que use os dois lados conhecidos. Por exemplo, se conhece CO e CA, use tan α = CO / CA. Calcule o valor da razão. Depois, você precisa encontrar qual ângulo α tem essa tangente. Isso pode ser feito:

     • Se o valor for de um ângulo notável (ex: tan α = 1), você sabe que α = 45°.

     • Se não for notável, você usaria uma calculadora científica (função tan⁻¹, arctan ou atan) ou consultaria uma tabela trigonométrica para encontrar o ângulo α.

   • O outro ângulo agudo (β) é β = 90° - α.

Exemplo Passo a Passo:

Problema: Um triângulo retângulo tem hipotenusa medindo 10 cm e um ângulo agudo de 30°. Resolva o triângulo.

Solução:

1. Informações: H = 10 cm, α = 30°.

2. Achar o outro ângulo (β): β = 90° - α = 90° - 30° = 60°.

3. Achar o Cateto Oposto a α (CO): Usamos seno. sen 30° = CO / H 1/2 = CO / 10 2 * CO = 10 → CO = 10 / 2 = 5 cm.

4. Achar o Cateto Adjacente a α (CA): Usamos cosseno. cos 30° = CA / H √3/2 = CA / 10 2 * CA = 10√3 → CA = (10√3) / 2 = 5√3 cm.

5. Resultado: Lados: 5 cm, 5√3 cm, 10 cm. Ângulos: 30°, 60°, 90°.

6. Aplicações Práticas da Trigonometria: Medindo o Mundo

A trigonometria no triângulo retângulo não é apenas um exercício acadêmico; ela tem aplicações incrivelmente úteis no mundo real, permitindo-nos medir coisas que seriam difíceis ou impossíveis de medir diretamente.

• Cálculo de Alturas Inacessíveis: Imagine que você quer saber a altura de um prédio alto ou de uma árvore. Você pode medir a distância horizontal do ponto onde você está até a base do objeto (Cateto Adjacente). Em seguida, usando um instrumento chamado teodolito (ou até um transferidor improvisado), você mede o ângulo de elevação – o ângulo formado entre a linha horizontal do seu olho e a linha de visão até o topo do objeto. Com o ângulo (α) e o Cateto Adjacente (CA), você pode usar a tangente para encontrar a altura (Cateto Oposto, CO): tan α = CO / CA → CO = CA * tan α. (Se necessário, some a altura do observador/instrumento ao resultado).

  <!-- Placeholder para imagem: Desenho de uma pessoa olhando para o topo de um prédio. Mostrar a distância horizontal (CA), a altura do prédio (CO), a linha de visão (Hipotenusa) e o ângulo de elevação (α) formado com a horizontal. Indicar a fórmula CO = CA * tan α. -->

• Cálculo de Distâncias Inacessíveis: Para medir a largura de um rio, você pode ficar em uma margem e identificar um ponto fixo (como uma árvore) na margem oposta. Caminhe uma distância conhecida ao longo da sua margem (Cateto Adjacente). Do ponto final, meça o ângulo formado entre a sua margem e a linha de visão até o ponto fixo na outra margem (α). Usando a tangente, você encontra a largura do rio (Cateto Oposto): tan α = CO / CA → CO = CA * tan α. Outra aplicação é usar o ângulo de depressão (ângulo formado entre a horizontal e a linha de visão para baixo) a partir de um ponto alto (como um farol) para calcular a distância até um objeto no nível do mar.

  <!-- Placeholder para imagem: Desenho da margem de um rio. Ponto A na margem, ponto P (árvore) na margem oposta. Caminha-se até o ponto B na mesma margem (distância AB = CA). Mede-se o ângulo α em B (ângulo PBA). A largura do rio (AP = CO) é encontrada por CO = CA * tan α. -->

• Navegação e Astronomia: A trigonometria é fundamental para determinar posições usando ângulos em relação a pontos de referência (estrelas, marcos terrestres), calcular distâncias e traçar rotas.

• Engenharia e Construção: Usada para calcular inclinações de rampas, telhados, forças em estruturas, projetos de pontes, etc.

• Física: Essencial para decompor vetores (como forças, velocidades) em componentes perpendiculares, facilitando a análise de movimentos e equilíbrios, especialmente em planos inclinados.

• Jogos e Computação Gráfica: Usada para calcular ângulos de visão, rotações de objetos, posicionamento em ambientes 3D, criando efeitos visuais realistas.

A capacidade de relacionar ângulos e lados torna a trigonometria uma ferramenta versátil e poderosa em muitas áreas do conhecimento e da tecnologia.

7. Resumo e Dicas Finais: Consolidando o Conhecimento

Exploramos os fundamentos da trigonometria no triângulo retângulo, uma ferramenta matemática poderosa que conecta ângulos e lados. Vamos recapitular os pontos essenciais:

Conceitos Chave:

• Triângulo Retângulo: Possui um ângulo de 90°. Lados: Hipotenusa (oposta ao 90°) e Catetos (formam o 90°).

• Cateto Oposto (CO) e Adjacente (CA): Dependem do ângulo agudo (α) de referência.

• Razões Trigonométricas:

  • Seno: sen α = CO / H

  • Cosseno: cos α = CA / H

  • Tangente: tan α = CO / CA (ou tan α = sen α / cos α)

• Relação Fundamental: sen²(α) + cos²(α) = 1

• Ângulos Complementares (α + β = 90°): sen α = cos β, cos α = sen β.

• Ângulos Notáveis (30°, 45°, 60°): Possuem valores de sen, cos, tan exatos e fáceis de deduzir/memorizar.

• Resolver Triângulos: Encontrar todos os lados e ângulos usando Pitágoras e as razões trigonométricas.

Dicas Importantes:

1. Identifique Corretamente: Sempre comece identificando a hipotenusa e, em seguida, os catetos oposto e adjacente em relação ao ângulo agudo com o qual você está trabalhando.

2. Escolha a Razão Certa: Selecione a razão (sen, cos ou tan) que relaciona o lado/ângulo que você quer encontrar com os lados/ângulos que você já conhece.

3. Tabela dos Notáveis: Memorize ou saiba deduzir rapidamente os valores para 30°, 45° e 60°. Isso agiliza muito!

4. Calculadora: Para ângulos não notáveis, use uma calculadora científica. Certifique-se de que ela está no modo correto (geralmente DEG para graus).

5. Desenhe: Sempre que possível, faça um esboço do triângulo e marque as informações conhecidas e o que você precisa encontrar. Isso ajuda a visualizar o problema.

8. Questões de Fixação

Para consolidar seu aprendizado, preparamos 15 exercícios que abordam os conceitos e aplicações da trigonometria no triângulo retângulo. Eles estão disponíveis em um arquivo separado, seguidos por suas resoluções detalhadas em outro arquivo. Desafie-se a resolvê-los!

9. Conclusão: A Porta de Entrada para um Mundo Maior

A trigonometria no triângulo retângulo é apenas o começo de uma jornada fascinante. Ela fornece as bases para entender conceitos mais avançados, como a trigonometria no ciclo trigonométrico, que lida com ângulos de qualquer medida, e as funções trigonométricas (senoide, cossenoide), essenciais em física, engenharia e muitas outras áreas.

Dominar o seno, o cosseno e a tangente no contexto do triângulo retângulo é uma habilidade valiosa que amplia sua capacidade de resolver problemas geométricos e de modelar situações do mundo real. Continue praticando, explorando diferentes tipos de problemas e você verá como a trigonometria pode ser uma ferramenta poderosa e elegante.

Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=D-E_A04ReTE

Canal: Gis com Giz Matemática

http://www.youtube.com/watch?v=C7NrVLmEYcs

Canal: Dicasdemat Sandro Curió