Propriedades das figuras geométricas

Explore o fascinante mundo das figuras geométricas e suas propriedades essenciais! Aprenda sobre lados, ângulos, vértices, simetria, área, volume e muito mais

Anderson Luiz Floriano Dos Santos

3/3/20257 min read

Introdução: A Arquitetura do Espaço – Desvendando as Propriedades das Figuras Geométricas

Desde os primórdios da civilização, o estudo das formas e do espaço tem sido fundamental para a compreensão do mundo ao nosso redor. As figuras geométricas são as entidades básicas desse estudo, e cada uma delas possui um conjunto único de propriedades que as definem e as distinguem umas das outras. Essas propriedades incluem características como o número de lados, a medida dos ângulos, a presença de simetria, a forma de calcular sua área ou volume, e muitas outras.

Nesta postagem abrangente, embarcaremos em uma jornada para desvendar as propriedades das figuras geométricas, tanto as planas (bidimensionais) quanto as espaciais (tridimensionais). Utilizaremos uma linguagem simples e didática, rica em exemplos e ilustrações, para que você possa compreender as características essenciais de cada forma e como essas propriedades se relacionam com o mundo físico. Seja você um estudante explorando os fundamentos da geometria ou alguém buscando aprofundar seus conhecimentos, este guia completo é para você!

1. Figuras Geométricas Planas: O Universo Bidimensional

As figuras geométricas planas são aquelas que possuem apenas duas dimensões: comprimento e largura. Elas existem em um plano e incluem polígonos (formados por segmentos de reta) e figuras curvas.

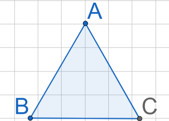
1.1. Triângulos:

Definição: Polígono com três lados e três ângulos.
Propriedades:
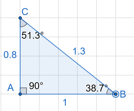
- A soma dos ângulos internos de um triângulo é sempre 180°.
- Classificação quanto aos lados:
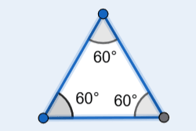
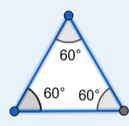
  - Equilátero: Três lados iguais e três ângulos iguais (60° cada). Possui 3 eixos de simetria.
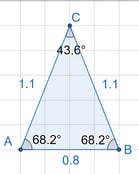
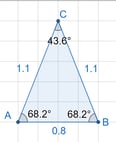
  - Isósceles: Dois lados iguais e dois ângulos iguais (os ângulos da base). Possui 1 eixo de simetria.
  - Escaleno: Três lados diferentes e três ângulos diferentes. Não possui eixos de simetria (a menos que seja degenerado).
- Classificação quanto aos ângulos:
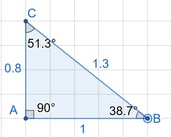
  - Retângulo: Possui um ângulo de 90°.
  - Acutângulo: Possui três ângulos agudos (menores que 90°).
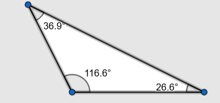
  - Obtusângulo: Possui um ângulo obtuso (maior que 90°).
- Possui 3 vértices.
- A área de um triângulo pode ser calculada por (base×altura) /2.

1.2. Quadriláteros:

Definição: Polígono com quatro lados e quatro ângulos.
Propriedades:
- A soma dos ângulos internos de um quadrilátero é sempre 360°.
- Paralelogramo: Lados opostos paralelos e iguais. Ângulos opostos iguais. Diagonais se intersectam no ponto médio.
  - Retângulo: Paralelogramo com quatro ângulos de 90°. Diagonais são iguais. Possui 2 eixos de simetria.
  - Losango: Paralelogramo com quatro lados iguais. Diagonais se intersectam perpendicularmente e bissectam os ângulos. Possui 2 eixos de simetria.
  - Quadrado: Paralelogramo com quatro lados iguais e quatro ângulos de 90°. Possui todas as propriedades do retângulo e do losango. Possui 4 eixos de simetria.
- Trapézio: Possui apenas um par de lados paralelos (bases).
  - Isósceles: Trapézio com lados não paralelos iguais.
  - Retângulo: Trapézio com dois ângulos retos.
- Deltoide (ou Papagaio): Possui dois pares de lados adjacentes iguais. Diagonais se intersectam perpendicularmente. Possui 1 eixo de simetria (a diagonal que liga os vértices dos ângulos diferentes).
- Possui 4 vértices e 2 diagonais.
- A área varia dependendo do tipo de quadrilátero.

1.3. Polígonos Regulares:

Definição: Polígonos com todos os lados iguais e todos os ângulos iguais.
Propriedades:
- Todos os lados têm o mesmo comprimento.
- Todos os ângulos internos têm a mesma medida.
- Possuem um centro a partir do qual todos os vértices estão à mesma distância (equidistantes).
- Possuem simetria rotacional e reflexiva (vários eixos de simetria).
- Exemplos: triângulo equilátero, quadrado, pentágono regular, hexágono regular, etc.
- A soma dos ângulos internos de um polígono regular de n lados é (n−2)×180°.
- Cada ângulo interno de um polígono regular de n lados mede ((n−2)×180°)/2.

1.4. Círculo:

Definição: Conjunto de todos os pontos em um plano que estão a uma distância fixa (raio) de um ponto central.
Propriedades:
- Possui um centro e um raio.
- O diâmetro é o dobro do raio (d=2r).
- A circunferência (o perímetro do círculo) é dada por C=2πr ou C=πd.
- A área do círculo é dada por A=πr².
- Possui infinitos eixos de simetria.
- Todos os raios têm o mesmo comprimento.
- Todos os diâmetros têm o mesmo comprimento.

2. Figuras Geométricas Espaciais: O Universo Tridimensional

As figuras geométricas espaciais são aquelas que possuem três dimensões: comprimento, largura e altura (ou profundidade). Elas ocupam volume no espaço.

2.1. Poliedros:

Definição: Sólidos geométricos cujas faces são polígonos planos.
Propriedades:
- Possuem faces, arestas (onde as faces se encontram) e vértices (onde as arestas se encontram).
- A relação de Euler para poliedros convexos é V−A+F=2, onde V é o número de vértices, A é o número de arestas e F é o número de faces.
- Prismas: Possuem duas bases paralelas e congruentes (polígonos) e faces laterais que são paralelogramos.
  - Reto: As faces laterais são retângulos.
  - Obliquo: As faces laterais são paralelogramos não retangulares.
  - O volume de um prisma é V=Area base×altura.
- Pirâmides: Possuem uma base poligonal e faces laterais triangulares que se encontram em um único vértice (ápice).
  - Reta: O ápice está diretamente acima do centro da base.
  - Oblíqua: O ápice não está diretamente acima do centro da base.
  - O volume de uma pirâmide é V=(1/3) × Area base × altura.
- Cubo (Hexaedro Regular): Prisma reto com seis faces quadradas congruentes. Possui 8 vértices, 12 arestas iguais e 6 faces iguais. Seu volume é V=aresta³.
- Paralelepípedo: Prisma reto com seis faces que são paralelogramos.
  - Reto (Bloco Retangular): Paralelepípedo com seis faces retangulares. Seu volume é V=comprimento×largura×altura.

2.2. Corpos Redondos:

Definição: Sólidos geométricos que possuem superfícies curvas.
Propriedades:
- Esfera: Conjunto de todos os pontos no espaço que estão a uma distância fixa (raio) de um ponto central.
  - Possui um centro e um raio.
  - Sua superfície é dada por A=4πr².
  - Seu volume é dado por V=(3/4) πr³.
  - Possui infinitos planos de simetria.
- Cilindro Circular Reto: Sólido gerado pela rotação de um retângulo em torno de um de seus lados. Possui duas bases circulares paralelas e congruentes e uma superfície lateral curva.
  - Possui um raio da base (r) e uma altura (h).
  - Sua área da superfície lateral é Alateral=2πrh.
  - Sua área total é Atotal=2πr(r+h).
  - Seu volume é V=πr²h.
- Cone Circular Reto: Sólido gerado pela rotação de um triângulo retângulo em torno de um de seus catetos. Possui uma base circular e uma superfície lateral curva que se encontra em um único vértice (ápice).
  - Possui um raio da base (r), uma altura (h) e uma geratriz (g=r2+h2).
  - Sua área da superfície lateral é Alateral=πrg.
  - Sua área total é Atotal=πr(r+g).
  - Seu volume é V=31πr2h.

3. Propriedades Fundamentais Comuns:

Além das propriedades específicas de cada figura, algumas propriedades são fundamentais e se aplicam a diversas formas geométricas:

Lados: Segmentos de reta que formam os polígonos.
Ângulos: Formados pela união de dois lados em um vértice. Podem ser internos ou externos
Vértices: Pontos onde os lados de um polígono se encontram.
Diagonais: Segmentos de reta que ligam dois vértices não adjacentes em um polígono.
Perímetro: A soma dos comprimentos de todos os lados de um polígono.
Área: A medida da superfície de uma figura plana.
Volume: A medida do espaço ocupado por uma figura espacial.
Simetria: A propriedade de uma figura permanecer inalterada sob certas transformações (reflexão, rotação, translação).
- Simetria de Reflexão (Axial): A figura pode ser dividida em duas partes que são imagens espelhadas uma da outra por uma linha (eixo de simetria).
- Simetria de Rotação: A figura pode ser rotacionada em torno de um ponto central por um certo ângulo (menor que 360°) e coincidir com sua posição original.
- Simetria de Translação: A figura pode ser deslocada em linha reta e coincidir com sua posição original (aplica-se a padrões repetitivos).

4. A Importância das Propriedades Geométricas:

O conhecimento das propriedades das figuras geométricas é essencial em diversas áreas:

Arquitetura e Engenharia: Para projetar edifícios, pontes e outras estruturas, considerando formas, áreas, volumes e estabilidade.
Design Gráfico e Arte: Para criar composições visuais equilibradas e esteticamente agradáveis, utilizando simetria e proporção.
Física e Matemática: Para modelar fenômenos naturais, calcular grandezas e resolver problemas.
Cartografia e Navegação: Para representar a Terra e orientar deslocamentos.
Indústria e Manufatura: Para criar objetos com dimensões e formas precisas.

Compreender as propriedades geométricas nos permite analisar o mundo ao nosso redor de forma mais precisa e resolver problemas práticos de maneira eficaz.

Conclusão: A Harmonia das Formas e do Espaço

As propriedades das figuras geométricas revelam a beleza e a ordem que permeiam o espaço ao nosso redor. Desde os simples polígonos planos até os complexos sólidos tridimensionais, cada forma possui características únicas que a definem e a tornam adequada para diferentes propósitos. Ao desvendar essas propriedades, não apenas aprimoramos nossa compreensão da matemática, mas também aguçamos nossa percepção do mundo que habitamos. Esperamos que este guia completo e didático tenha iluminado o fascinante universo das figuras geométricas e suas propriedades, inspirando você a explorar ainda mais a harmonia das formas e do espaço!