Perímetro de figuras planas
Perímetros Desvendados: Guia Completo para o Ensino Fundamental
Você já se perguntou como calcular a quantidade de cerca necessária para cercar um terreno? Ou quanto de moldura é preciso para emoldurar um quadro? Ou ainda, como os arquitetos determinam a quantidade exata de rodapé necessário para uma sala? A resposta para essas e muitas outras questões está no estudo do Perímetro, um dos conceitos mais importantes e práticos da geometria plana.
Neste artigo, vamos explorar todos os aspectos desse tema fascinante, com explicações simples, exemplos práticos e imagens ilustrativas para facilitar seu entendimento. Prepare-se para descobrir como o cálculo de perímetros está presente em nosso dia a dia e como ele pode ser aplicado para resolver problemas reais!
O que é Perímetro
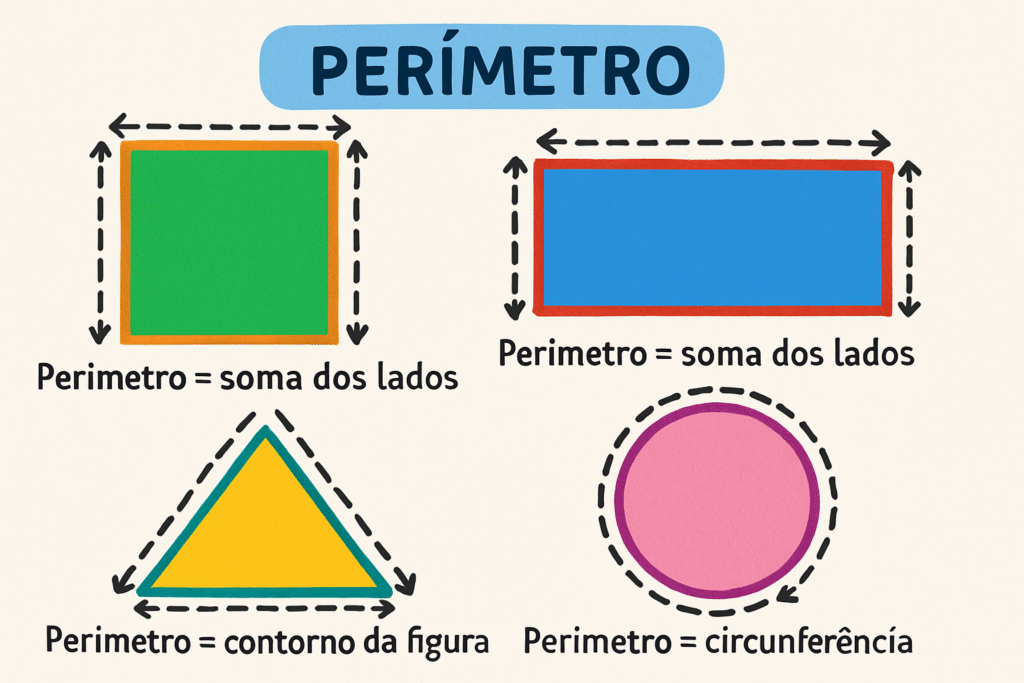
O perímetro é a medida do contorno de uma figura plana, ou seja, é o comprimento total da linha que delimita a figura. Em termos mais simples, é a soma dos comprimentos de todos os lados de uma figura.
Imagine uma cerca ao redor de um terreno: o perímetro representa o comprimento total dessa cerca. Ou pense em uma pulseira: o perímetro é o comprimento total da pulseira, que determina se ela cabe no seu pulso.
Unidades de Medida de Perímetro
As unidades de medida de perímetro são as mesmas utilizadas para medir comprimento. No Sistema Internacional de Unidades (SI), a unidade padrão é o metro (m), mas também são comumente utilizadas:
Quilômetro (km): 1 km = 1.000 m
Centímetro (cm): 1 m = 100 cm
Milímetro (mm): 1 m = 1.000 mm
É importante notar que a soma de todos os lados é uma medida unidimensional (de comprimento), diferente da área, que é bidimensional (de superfície). Por isso, o perímetro é sempre expresso em unidades lineares (m, cm, km), enquanto a área é expressa em unidades quadradas (m², cm², km²).
Diferença entre Perímetro e Área
Muitas vezes, os conceitos de perímetro e área são confundidos. Para entender a diferença:
Perímetro: Mede o contorno, a fronteira da figura (comprimento).
Área: Mede a superfície, o espaço interno da figura (superfície).
Por exemplo, se pensarmos em um campo de futebol:
O perímetro seria a distância total ao redor do campo (o comprimento da linha que delimita o campo).
A área seria o espaço dentro do campo (a superfície onde os jogadores correm).
Perímetro de Polígonos Regulares
Os polígonos regulares são figuras planas fechadas formadas por segmentos de reta (lados), onde todos os lados têm o mesmo comprimento e todos os ângulos internos são iguais.
O perímetro de um polígono regular pode ser calculado multiplicando-se o comprimento de um lado pelo número de lados:
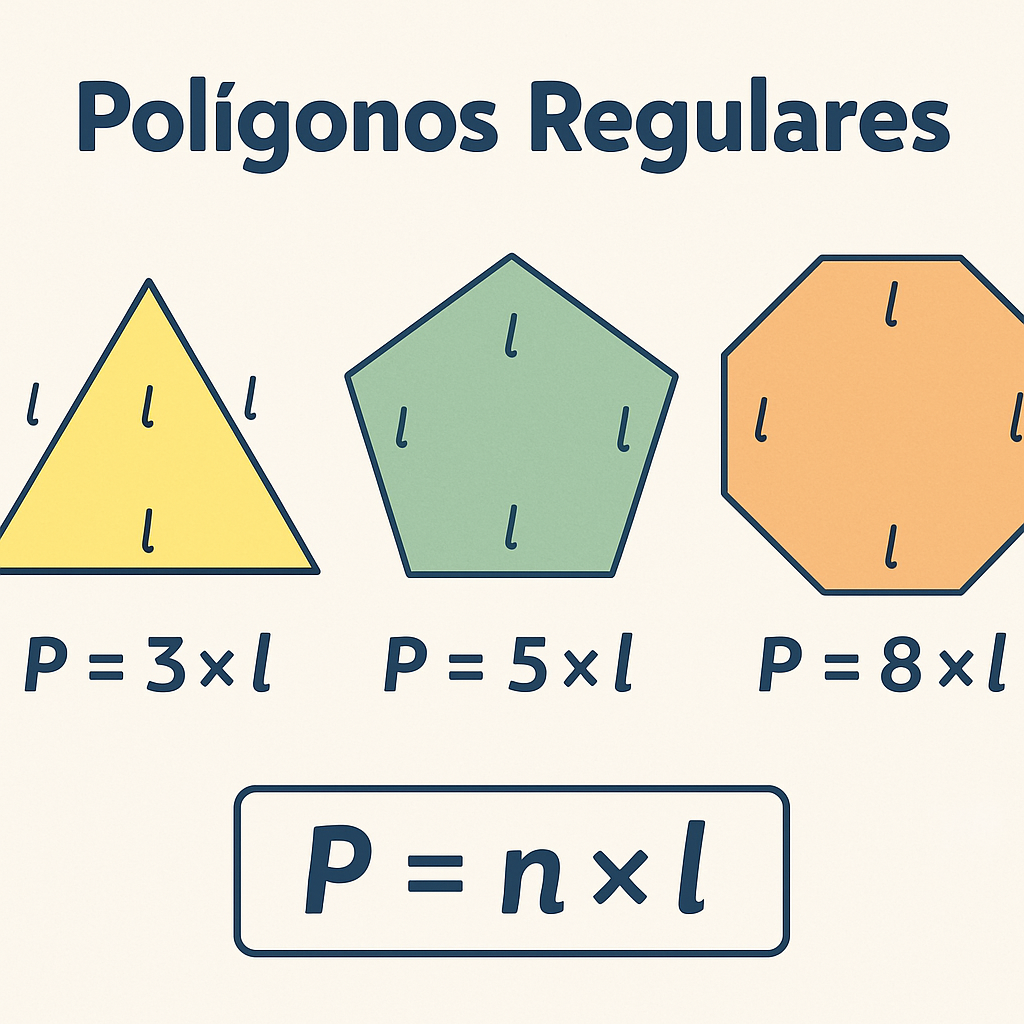
P = n × l
Onde:
P é o perímetro
n é o número de lados
l é o comprimento de cada lado
Exemplo: Um hexágono regular (6 lados) com lados de 5 cm tem perímetro P = 6 × 5 = 30 cm.
Esta fórmula é válida para qualquer polígono regular, independentemente do número de lados. A seguir, veremos casos específicos de polígonos comuns.
Perímetro do Quadrado
O quadrado é um polígono regular com 4 lados iguais e 4 ângulos retos (90°).
O perímetro de um quadrado é calculado multiplicando-se o comprimento do lado por 4:
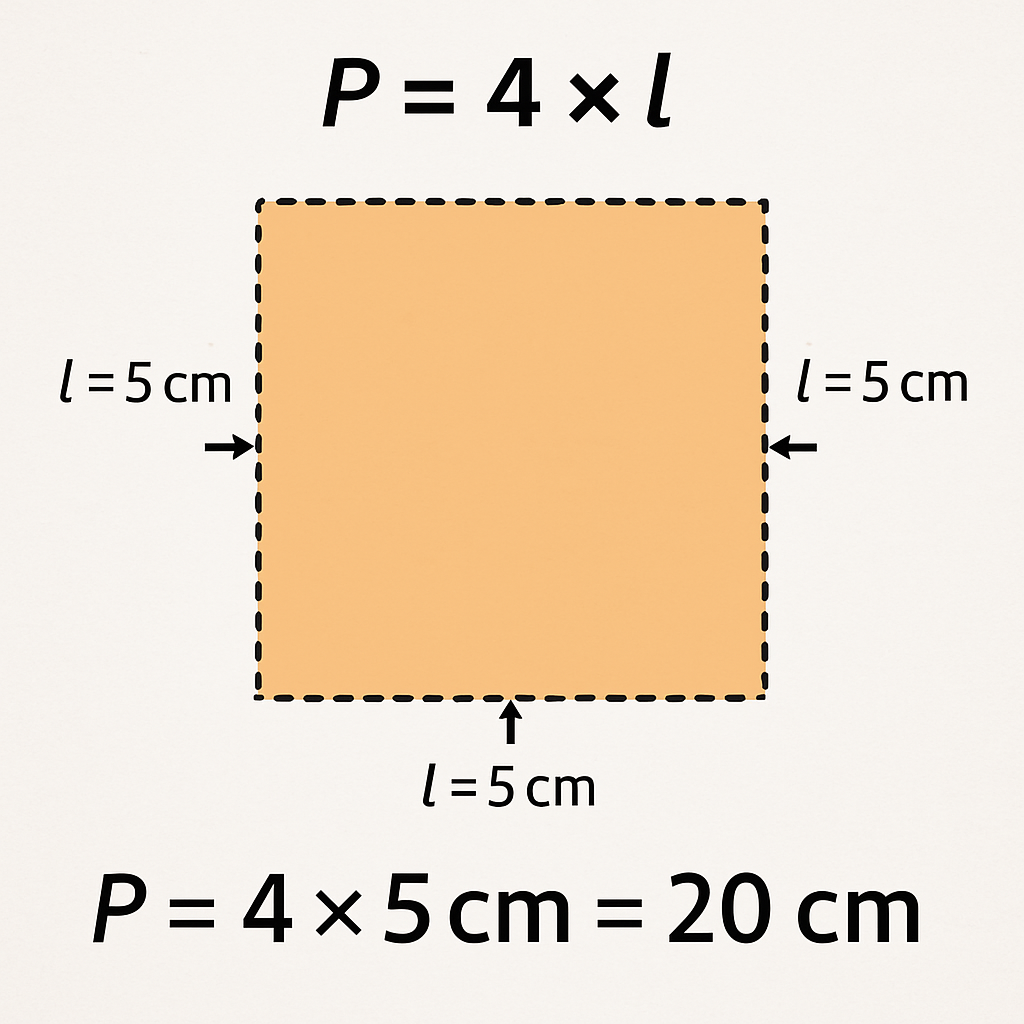
P = 4 × l
Onde:
P é o perímetro
l é o comprimento do lado
Exemplo: Um quadrado com lado de 7 cm tem perímetro P = 4 × 7 = 28 cm.
Uma característica interessante do quadrado é que, conhecendo apenas uma medida (o lado), podemos calcular tanto o perímetro quanto a área.
Perímetro do Retângulo
O retângulo é um quadrilátero (polígono de 4 lados) com 4 ângulos retos (90°). Diferente do quadrado, o retângulo tem lados opostos iguais, mas lados adjacentes podem ter comprimentos diferentes.
O perímetro de um retângulo é calculado somando-se todos os seus lados, ou, de forma mais prática, usando a fórmula:
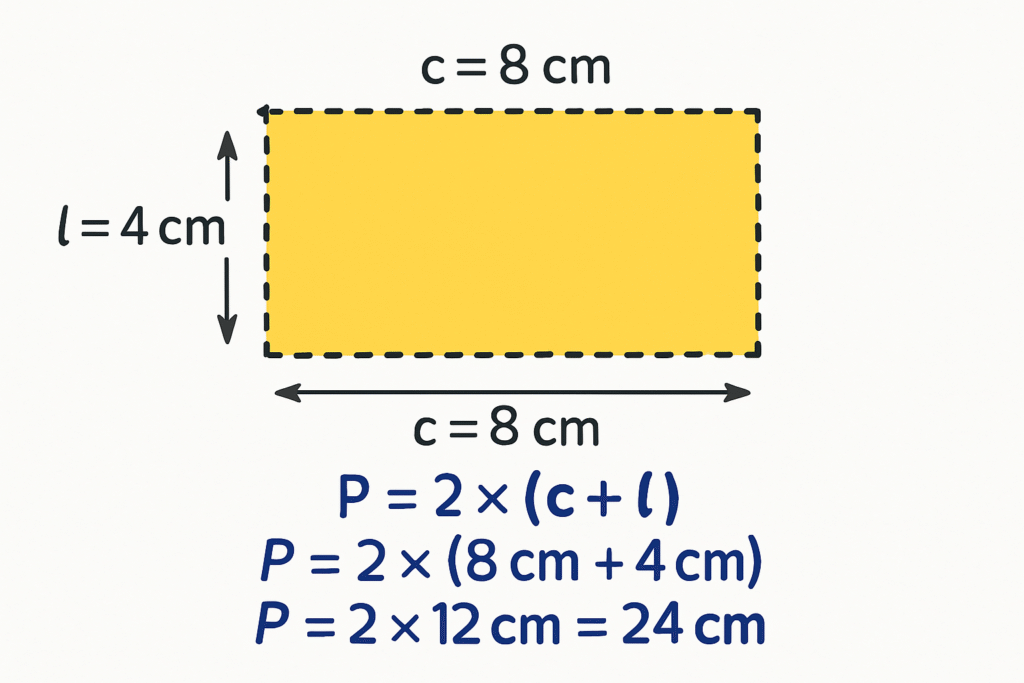
P = 2 × (c + l)
Onde:
P é o perímetro
c é o comprimento
l é a largura
Exemplo: Um retângulo com comprimento de 8 cm e largura de 5 cm tem perímetro P = 2 × (8 + 5) = 2 × 13 = 26 cm.
O retângulo é uma das figuras mais comuns no nosso cotidiano, presente em livros, mesas, portas, janelas, telas de celular, entre outros objetos.
Perímetro do Triângulo
O triângulo é um polígono com 3 lados. Existem diferentes tipos de triângulos, classificados de acordo com seus lados e ângulos:
Triângulo equilátero: Todos os lados têm o mesmo comprimento.
Triângulo isósceles: Dois lados têm o mesmo comprimento.
Triângulo escaleno: Todos os lados têm comprimentos diferentes.
O perímetro de qualquer triângulo é calculado somando-se os comprimentos de seus três lados:
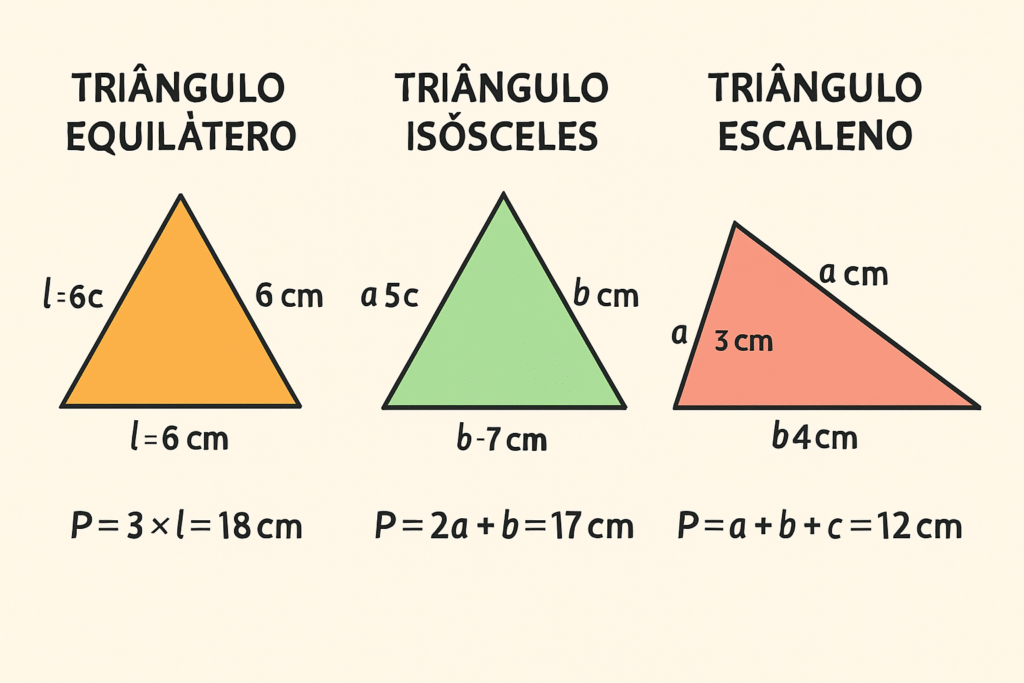
P = a + b + c
Onde:
P é o perímetro
a, b e c são os comprimentos dos lados
Exemplo: Um triângulo com lados de 5 cm, 7 cm e 9 cm tem perímetro P = 5 + 7 + 9 = 21 cm.
Casos Especiais de Triângulos
Para o triângulo equilátero, onde todos os lados têm o mesmo comprimento, o perímetro pode ser calculado de forma mais simples:
P = 3 × l
Onde:
P é o perímetro
l é o comprimento de cada lado
Exemplo: Um triângulo equilátero com lado de 6 cm tem perímetro P = 3 × 6 = 18 cm.
Perímetro de Outros Polígonos
Além dos polígonos já mencionados, existem muitos outros, como pentágonos (5 lados), hexágonos (6 lados), heptágonos (7 lados), octógonos (8 lados), etc.
Para calcular o perímetro de qualquer polígono, basta somar os comprimentos de todos os seus lados:
P = l₁ + l₂ + l₃ + … + lₙ
Onde:
P é o perímetro
l₁, l₂, l₃, …, lₙ são os comprimentos dos lados
Para polígonos regulares, como já vimos, podemos usar a fórmula simplificada P = n × l, onde n é o número de lados e l é o comprimento de cada lado.
Exemplo: Um pentágono regular (5 lados) com lados de 4 cm tem perímetro P = 5 × 4 = 20 cm.
Perímetro do Círculo
O círculo não é um polígono, pois não é formado por segmentos de reta, mas por uma curva fechada onde todos os pontos estão à mesma distância de um ponto central (o centro do círculo).
O perímetro de um círculo é chamado de circunferência e pode ser calculado usando a seguinte fórmula:
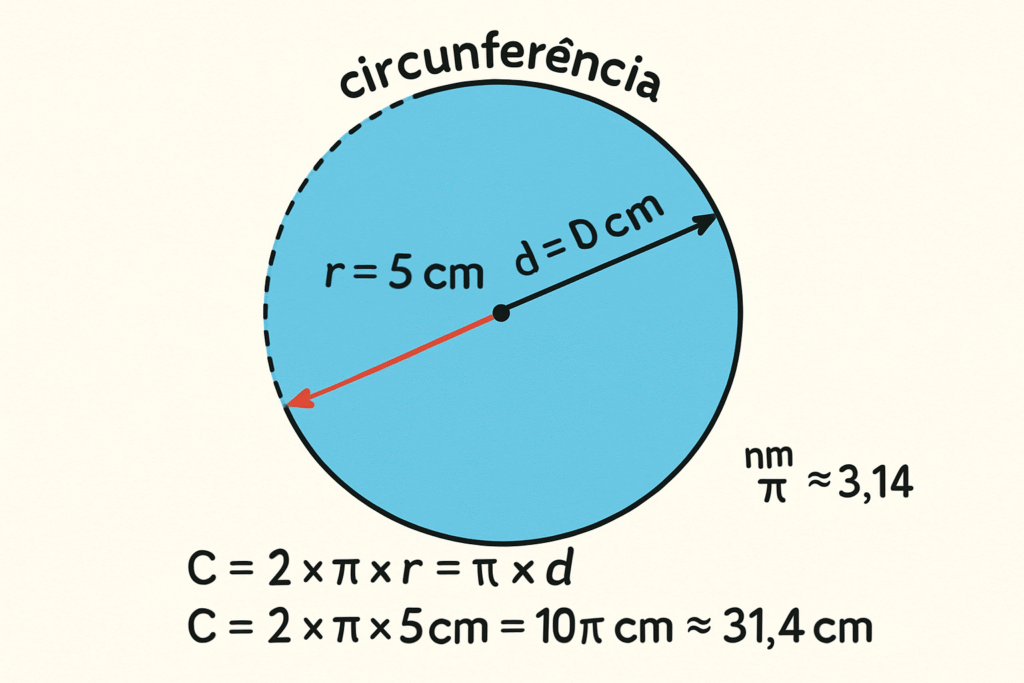
C = 2 × π × r
ou
C = π × d
Onde:
C é a circunferência (perímetro)
π (pi) é aproximadamente 3,14159…
r é o raio do círculo
d é o diâmetro do círculo (d = 2 × r)
Exemplo: Um círculo com raio de 5 cm tem circunferência C = 2 × π × 5 = 10π ≈ 31,42 cm.
É importante lembrar que o diâmetro de um círculo é sempre o dobro do raio, e que π é uma constante matemática que representa a razão entre a circunferência e o diâmetro de qualquer círculo.
Perímetro de Figuras Compostas
Muitas vezes, nos deparamos com figuras que são compostas por várias figuras geométricas básicas. Para calcular o perímetro dessas figuras compostas, precisamos identificar o contorno externo completo.
Existem duas abordagens principais:
1. Decomposição
Podemos decompor a figura em figuras mais simples, calcular o perímetro de cada uma delas e depois somar as partes que formam o contorno externo, tendo cuidado para não contar duas vezes os segmentos internos.
2. Soma Direta
Podemos identificar e medir cada segmento que forma o contorno externo da figura e somá-los diretamente.
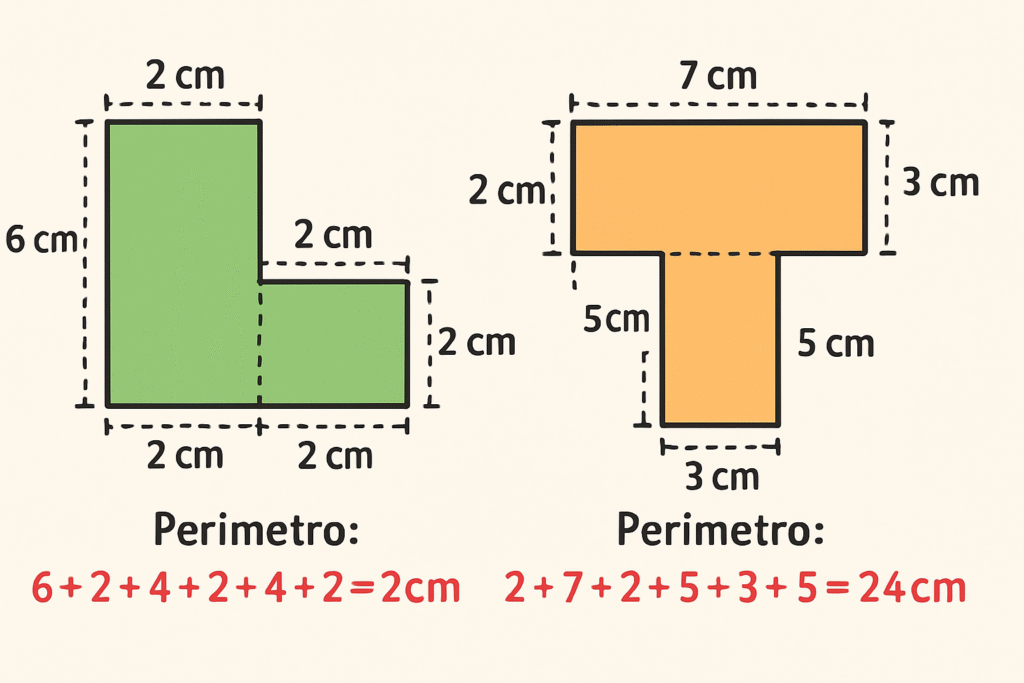
Exemplo: Considere uma figura em forma de “L”, formada por dois retângulos: um de 5 cm × 3 cm e outro de 2 cm × 4 cm. O perímetro dessa figura seria a soma de todos os segmentos do contorno externo, que é 18 cm.
É importante observar que, ao calcular o perímetro de figuras compostas, devemos considerar apenas o contorno externo, ignorando as linhas internas onde as figuras se encontram.
Relação entre Perímetro e Escala
Quando trabalhamos com mapas, plantas ou modelos em escala, é importante entender como o perímetro é afetado pela escala.
Se uma figura é ampliada ou reduzida por um fator de escala k, seu perímetro também é ampliado ou reduzido pelo mesmo fator:
P₂ = k × P₁
Onde:
P₁ é o perímetro original
P₂ é o perímetro após a mudança de escala
k é o fator de escala
Exemplo: Se uma planta de uma casa tem perímetro de 40 cm na escala 1:100, o perímetro real da casa será 40 × 100 = 4.000 cm = 40 m.
Esta relação é linear, diferente da relação entre escala e área, que é quadrática (a área é afetada pelo quadrado do fator de escala).
Aplicações Práticas do Cálculo
O cálculo de perímetros tem inúmeras aplicações práticas em nosso dia a dia e em diversas áreas profissionais:
Na Construção Civil
Cercamento de terrenos: Calcular a quantidade de cerca, muro ou grade necessária para cercar um terreno.
Instalação de rodapés: Determinar a quantidade de rodapé necessária para uma sala.
Molduras e acabamentos: Calcular o comprimento de molduras para portas, janelas e outros elementos arquitetônicos.
Na Agricultura
Irrigação por gotejamento: Determinar o comprimento de tubulação necessária para irrigar o perímetro de uma plantação.
Cercamento de pastos: Calcular a quantidade de cerca necessária para delimitar áreas de pastagem.
Controle de pragas: Estabelecer barreiras de proteção ao redor de cultivos.
No Design e Decoração
Molduras para quadros e espelhos: Calcular o comprimento de moldura necessária.
Bordas decorativas: Determinar o comprimento de bordas para mesas, tapetes e outros elementos decorativos.
Fitas e acabamentos: Calcular a quantidade de fita necessária para acabamentos em cortinas, almofadas, etc.
No Esporte
Demarcação de campos: Calcular o comprimento de linhas para demarcar campos esportivos.
Pistas de corrida: Determinar o comprimento de pistas de atletismo e outros circuitos.
Cordas e redes: Calcular o comprimento de cordas para redes de vôlei, tênis, etc.
Na Saúde
Medidas corporais: O perímetro é usado para medir circunferências corporais, como cintura, quadril, braço, etc.
Avaliação física: Essas medidas são importantes para avaliação física e acompanhamento de saúde.
Estas aplicações demonstram como o conhecimento sobre perímetros transcende a sala de aula e tem impacto direto em diversos aspectos de nossas vidas.
Como Resolver Problemas de Perímetro
Para resolver problemas envolvendo este conceito, podemos seguir uma abordagem sistemática:
1. Identificar a Figura Geométrica
O primeiro passo é identificar qual figura geométrica está envolvida no problema. Isso determinará qual fórmula de perímetro deve ser utilizada.
2. Identificar os Dados Fornecidos
Verifique quais informações são fornecidas no problema: comprimentos de lados, raios, diâmetros, etc.
3. Escolher a Fórmula Adequada
Selecione a fórmula de perímetro apropriada para a figura identificada:
Quadrado: P = 4 × l
Retângulo: P = 2 × (c + l)
Triângulo: P = a + b + c
Polígono regular: P = n × l
Círculo: C = 2 × π × r
4. Substituir os Valores e Calcular
Substitua os valores conhecidos na fórmula e realize os cálculos necessários. Lembre-se de verificar se todas as unidades estão consistentes.
5. Verificar a Unidade de Medida
O resultado do cálculo de perímetro deve ser expresso em unidades lineares (m, cm, km, etc.).
6. Interpretar o Resultado
Analise se o resultado obtido faz sentido no contexto do problema. Um perímetro negativo ou excessivamente grande/pequeno pode indicar um erro de cálculo.
Dicas Adicionais
Conversão de unidades: Muitas vezes é necessário converter entre diferentes unidades de comprimento. Lembre-se das relações: 1 m = 100 cm = 1.000 mm, 1 km = 1.000 m.
Figuras compostas: Para figuras complexas, considere decompô-las em figuras mais simples e calcular o perímetro do contorno externo.
Uso de diagramas: Desenhar a figura e anotar as medidas conhecidas pode ajudar a visualizar o problema e evitar erros.
Seguindo estes passos e dicas, você estará bem equipado para resolver uma ampla variedade de problemas envolvendo perímetros.
Conclusão: A Importância do Estudo de Perímetros
O estudo dos perímetros é uma parte fundamental da geometria plana, com aplicações que vão muito além da sala de aula. Desde a antiguidade, quando civilizações antigas precisavam medir o contorno de terras para agricultura, até os dias atuais, com cálculos precisos para construção civil e design, o conceito de perímetro tem sido essencial para o desenvolvimento humano.
Compreender como calcular o perímetro de diferentes figuras geométricas nos permite:
Resolver problemas práticos do cotidiano
Tomar decisões mais informadas em projetos de construção e design
Entender melhor o mundo bidimensional em que vivemos
Desenvolver o raciocínio espacial e a capacidade de visualização
As fórmulas que aprendemos neste artigo – para quadrados, retângulos, triângulos, polígonos regulares e círculos – são ferramentas poderosas que nos permitem quantificar e comparar o contorno de diferentes objetos e estruturas.
Ao dominar o cálculo de perímetros, você adquire uma habilidade matemática que tem aplicações práticas imediatas e que serve como base para estudos mais avançados em áreas como geometria analítica, cálculo e física.
Agora que você compreende os princípios fundamentais do cálculo de perímetros, está pronto para praticar com os exercícios a seguir e consolidar seu aprendizado.
Algumas video- aulas sobre o assunto:
http://www.youtube.com/watch?v=H7RIM8RRr_A
Canal: Matemática do Zero – Raffaías Santos
http://www.youtube.com/watch?v=dArATPsuLjM
Canal: Gis com Giz Matemática
