Pitágoras: O Filósofo que Revolucionou a Matemática e Moldou o Pensamento Ocidental

Introdução: Desvendando o Legado de um Gênio Grego

No vasto panteão de pensadores que moldaram a civilização ocidental, poucos nomes ressoam com a mesma intensidade e mistério que o de Pitágoras de Samos. Frequentemente associado ao famoso teorema que atormenta (e ilumina) estudantes de geometria há milênios, Pitágoras foi muito mais do que um matemático. Ele foi um filósofo profundo, um místico enigmático, um líder carismático e, acima de tudo, uma figura central na transição do pensamento mítico para o racional na Grécia Antiga. Sua influência estende-se da matemática à música, da astronomia à ética, deixando um legado complexo e duradouro que continua a fascinar e inspirar.

Mas quem foi realmente Pitágoras? Para além do teorema, que ideias revolucionárias ele propôs? Como sua escola, uma mistura peculiar de comunidade científica e seita religiosa, impactou o desenvolvimento do conhecimento? Neste artigo, embarcaremos em uma jornada pela história, explorando a vida, as contribuições e o pensamento deste gigante intelectual. Investigaremos suas origens, suas supostas viagens em busca de sabedoria, a fundação de sua influente escola na Magna Grécia e, claro, suas descobertas matemáticas que não apenas revolucionaram a disciplina, mas também buscaram decifrar a própria harmonia do cosmos. Convidamos você, estudante, entusiasta da matemática ou simplesmente curioso, a desvendar conosco os segredos e a genialidade de Pitágoras, o filósofo que viu nos números a chave para compreender o universo.

Quem Foi Pitágoras? Traçando o Perfil do Sábio de Samos

A figura histórica de Pitágoras emerge das brumas do tempo, envolta em lendas e relatos nem sempre convergentes. Separar o homem do mito é um desafio, dado que ele próprio parece ter cultivado uma aura de mistério e que nenhum escrito de sua autoria sobreviveu até nós. O que sabemos advém principalmente de biógrafos e filósofos posteriores, como Heródoto, Platão, Aristóteles e Diógenes Laércio, cujas narrativas, embora valiosas, foram escritas séculos depois e muitas vezes misturam fatos com hagiografia.

Origens e Juventude em Samos: O Berço de um Pensador

Pitágoras nasceu por volta de 570 a.C. na ilha de Samos, uma próspera pólis grega no Mar Egeu, próxima à costa da Jônia (atual Turquia). Samos era, na época, um vibrante centro comercial e cultural, o que certamente proporcionou ao jovem Pitágoras um ambiente estimulante. Relatos tradicionais indicam que seu pai era Mnesarco, um mercador ou um gravador de gemas, possivelmente de origem fenícia, e sua mãe, Pythais, uma nativa de Samos. Algumas lendas posteriores chegam a atribuir-lhe uma concepção divina, ligando-o ao deus Apolo, o que reforça a veneração que o cercava.

Sua educação inicial provavelmente seguiu os moldes da elite grega da época, incluindo estudos em música (lira), poesia e atletismo. Mais significativo, porém, pode ter sido o contato com as correntes filosóficas que floresciam na Jônia. Há indícios, embora não conclusivos, de que Pitágoras possa ter sido discípulo ou ao menos conhecido figuras proeminentes como Tales de Mileto, o "pai da filosofia ocidental", e seu sucessor, Anaximandro. Se verdadeiros, esses encontros teriam exposto Pitágoras às primeiras tentativas de explicar o universo através da razão e da observação, buscando um princípio fundamental (a arché) para toda a existência, uma busca que marcaria profundamente seu próprio pensamento.

Viagens em Busca de Sabedoria: Rumo ao Egito e à Babilônia?

A tradição biográfica pitagórica é rica em relatos sobre longas viagens que o filósofo teria empreendido em busca de conhecimento, passando décadas longe de Samos. Os destinos mais citados são o Egito e a Babilônia, centros de antigas e renomadas tradições matemáticas, astronômicas e religiosas. No Egito, ele teria se aprofundado nos mistérios sacerdotais, na geometria prática utilizada para demarcar terras após as cheias do Nilo e na complexa cosmologia egípcia. Na Babilônia, acredita-se que tenha absorvido conhecimentos avançados de aritmética, álgebra e astronomia, incluindo observações celestes e métodos de cálculo.

Outras tradições mencionam ainda viagens à Fenícia, Síria, Pérsia e até mesmo à Índia. Embora a historicidade e a duração exata dessas viagens sejam debatidas por especialistas – alguns veem nelas um embelezamento posterior para justificar a amplitude dos conhecimentos pitagóricos –, é inegável que o pensamento de Pitágoras incorpora elementos que sugerem contato com culturas orientais, como a crença na transmigração das almas (metempsicose) e certas práticas ascéticas. Independentemente da veracidade literal das viagens, elas simbolizam a busca incessante de Pitágoras por uma sabedoria universal, integrando conhecimentos de diversas fontes.

O Estabelecimento em Crotona: Nascimento de uma Comunidade Filosófica

Por volta de 530 a.C., Pitágoras, já um homem maduro e possuidor de vasto conhecimento, deixou Samos. A razão mais provável para sua partida foi a crescente tirania de Polícrates, governante de Samos, cujo regime opressor poderia ser incompatível com a independência intelectual e as aspirações de Pitágoras. Ele dirigiu-se à Magna Grécia, a região do sul da Itália colonizada por gregos, estabelecendo-se na cidade de Crotona (atual Crotone, na Calábria).

Crotona era uma cidade florescente, conhecida por sua escola de medicina e por seus atletas vitoriosos nos Jogos Olímpicos. Foi ali que Pitágoras encontrou terreno fértil para disseminar suas ideias e fundar sua famosa escola, que era, na verdade, muito mais que uma instituição de ensino: era uma comunidade filosófica, científica e religiosa, com forte influência política. A chegada de Pitágoras a Crotona marca o início da fase mais documentada e influente de sua vida, onde suas ideias matemáticas e filosóficas ganhariam forma e seus seguidores se multiplicariam, dando origem ao movimento pitagórico.

A Escola Pitagórica: Mais que Matemática, um Modo de Vida

A comunidade fundada por Pitágoras em Crotona transcendia em muito a noção moderna de uma escola. Era uma irmandade (hetaireia), um centro de estudos intelectuais, uma comunidade religiosa e, em certa medida, uma força política. A influência de Pitágoras e seus seguidores rapidamente se espalhou pela Magna Grécia, atraindo discípulos das famílias aristocráticas locais, ansiosos por participar dessa nova forma de vida dedicada à busca da sabedoria e da purificação.

Fundação e Princípios: A Busca pela Harmonia Interior e Cósmica

A Escola Pitagórica, ou Ordem Pitagórica, baseava-se em princípios filosóficos e religiosos profundos. O objetivo central era a purificação da alma (katharsis) para libertá-la do ciclo de reencarnações (metempsicose) e alcançar uma união com o divino. Para os pitagóricos, essa purificação não se dava apenas por rituais religiosos tradicionais, mas principalmente através do estudo intelectual, da contemplação da ordem do cosmos e de uma vida regrada e virtuosa.

A matemática, a música e a astronomia não eram vistas apenas como disciplinas acadêmicas, mas como caminhos para compreender a estrutura harmoniosa e racional do universo. Acreditava-se que, ao desvendar as leis numéricas que regem o cosmos, a alma humana poderia espelhar essa harmonia e ordem, purificando-se no processo. A vida comunitária era essencial, com bens muitas vezes compartilhados e um forte senso de lealdade e fraternidade entre os membros.

A Filosofia Pitagórica: "Tudo é Número"

O cerne da filosofia pitagórica reside na célebre, embora possivelmente simplificada, máxima: "Tudo é número". Para Pitágoras e seus seguidores, os números não eram meras abstrações ou ferramentas de contagem, mas os próprios princípios constitutivos da realidade. Eles acreditavam que a essência de todas as coisas, desde os corpos celestes até as notas musicais e as virtudes morais, podia ser expressa através de relações numéricas.

Cada número possuía um significado simbólico e qualitativo. O número 1 (a mônada) representava a unidade primordial, a origem de tudo. O 2 (a díade) simbolizava a dualidade, a divisão, o feminino. O 3 representava a harmonia (união da unidade e da dualidade), o masculino. O 4 simbolizava a justiça e a solidez (associado ao quadrado). A soma dos quatro primeiros números (1+2+3+4 = 10), a tetraktys, era especialmente sagrada, vista como um símbolo da perfeição do universo e da harmonia cósmica. A tetraktys era representada por um triângulo equilátero com dez pontos e servia como base para juramentos solenes.

Essa visão numérica do universo levava a uma busca incessante por padrões e proporções matemáticas na natureza. Acreditavam que compreender essas relações era compreender a própria estrutura da realidade e a mente do Criador (ou Demiurgo).

A Crença na Transmigração das Almas (Metempsicose)

Um dos aspectos mais distintivos e, para muitos gregos da época, exóticos do pitagorismo era a crença na metempsicose, a doutrina da reencarnação ou transmigração das almas. Influenciada possivelmente por tradições órficas ou orientais, essa crença postulava que a alma é imortal e, após a morte do corpo, migra para outro corpo, seja humano, animal ou até mesmo vegetal, dependendo do grau de pureza alcançado na vida anterior.

O objetivo final era escapar desse ciclo de renascimentos através de uma vida dedicada à filosofia, ao estudo e à prática de virtudes. A purificação da alma, alcançada pelo conhecimento da ordem numérica do cosmos e por um comportamento ético, permitiria à alma retornar à sua origem divina. Essa crença tinha implicações práticas profundas no modo de vida pitagórico, incluindo restrições alimentares (como o vegetarianismo, embora haja debates sobre sua universalidade na escola) e a ênfase na memória e no autoconhecimento como formas de recordar vidas passadas e aprender com elas.

O Modo de Vida Pitagórico: Regras, Rituais e Segredo

A vida na comunidade pitagórica era estritamente regulada por um conjunto de preceitos e proibições conhecidos como akousmata (coisas ouvidas) ou symbola (símbolos, senhas). Essas regras abrangiam diversos aspectos da vida cotidiana, desde a dieta e o vestuário até o comportamento social e os rituais religiosos. Alguns exemplos famosos (e por vezes enigmáticos) incluem:

•Abster-se de comer favas (talvez por razões religiosas, de saúde ou simbólicas).

•Não remexer o fogo com uma faca (não provocar quem está irado).

•Não quebrar o pão (não dividir os amigos).

•Calçar primeiro o sapato direito.

•Não falar sem luz.

•Apagar as cinzas ao retirar a panela do fogo (apagar os vestígios da raiva).

Além dessas regras, a escola era marcada por um forte senso de hierarquia e segredo. Os discípulos eram divididos em diferentes níveis. Os akousmatikoi (ouvintes) eram os iniciantes, que recebiam os ensinamentos de forma dogmática e se concentravam nos aspectos práticos e morais da doutrina. Após um período de provação e silêncio (que podia durar anos), os mais aptos poderiam se tornar mathematikoi (estudantes, aprendizes), tendo acesso aos ensinamentos mais profundos sobre matemática, música, astronomia e filosofia, diretamente do mestre ou dos discípulos mais avançados. A divulgação dos conhecimentos mais esotéricos para não iniciados era estritamente proibida, vista como uma profanação.

Essa combinação de rigor intelectual, disciplina moral, misticismo religioso e sigilo conferiu à Escola Pitagórica uma aura única e poderosa, mas também a tornou alvo de suspeitas e, eventualmente, perseguições.

As Revoluções Matemáticas de Pitágoras: Desvendando a Ordem Numérica

Embora a Escola Pitagórica fosse um complexo centro filosófico e religioso, é inegável que suas contribuições mais duradouras e universalmente reconhecidas residem no campo da matemática. Para Pitágoras e seus seguidores, a matemática era a linguagem do universo, a chave para desvendar a ordem subjacente a toda a realidade. Eles não apenas utilizaram conhecimentos matemáticos herdados de egípcios e babilônios, mas os elevaram a um novo patamar de abstração, rigor e generalização, lançando as bases para muito do que hoje entendemos como matemática pura.

O Famoso Teorema de Pitágoras: Mais que um Triângulo Retângulo

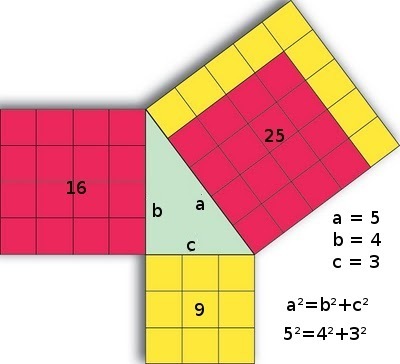
Nenhuma descoberta matemática está tão intrinsecamente ligada ao nome de Pitágoras quanto o teorema que leva seu nome. Afirmando que, em qualquer triângulo retângulo, o quadrado da medida da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados das medidas dos catetos (os lados que formam o ângulo reto), ou seja, a² + b² = c², este teorema é uma pedra angular da geometria euclidiana e possui inúmeras aplicações práticas e teóricas.

É importante notar que a relação expressa pelo teorema já era conhecida empiricamente por civilizações anteriores, como os babilônios e talvez os egípcios, que utilizavam ternos de números que satisfaziam a relação (como 3, 4 e 5) para construir ângulos retos em suas edificações e demarcações de terra. No entanto, a grande contribuição atribuída aos pitagóricos (ou talvez ao próprio Pitágoras) foi a demonstração formal e geral do teorema, provando que ele era válido para todos os triângulos retângulos, e não apenas para casos específicos. Essa busca por provas lógicas e universais, em vez de meras constatações práticas, representa uma mudança fundamental na natureza do pensamento matemático, característica da abordagem grega.

Existem diversas demonstrações possíveis para o Teorema de Pitágoras, algumas visuais e outras algébricas. Uma demonstração visual clássica envolve a construção de quadrados sobre cada um dos lados do triângulo retângulo e a reorganização das áreas para mostrar a equivalência. (Poderíamos incluir aqui uma descrição simplificada ou uma imagem ilustrativa posteriormente). A beleza e a universalidade do teorema residem em sua capacidade de conectar álgebra (a equação) e geometria (as formas) de maneira elegante e fundamental.

Sua importância transcende a geometria básica. O teorema é fundamental para a definição de distância no plano cartesiano, para a trigonometria (através da identidade fundamental sen²θ + cos²θ = 1), para a física (no cálculo de vetores e trajetórias) e para inúmeras outras áreas da ciência e da engenharia. É um testemunho do poder da abstração matemática e da busca pitagórica pela ordem numérica no mundo.

Contribuições à Teoria dos Números: Explorando as Propriedades Intrínsecas

O fascínio pitagórico pelos números ia muito além da geometria. Eles foram pioneiros no estudo das propriedades intrínsecas dos números inteiros, dando origem ao que hoje chamamos de Teoria dos Números. Investigaram conceitos como:

•Números Pares e Ímpares: Classificaram os números e exploraram suas interações em operações aritméticas.

•Números Primos e Compostos: Reconheceram a importância dos números primos como "blocos de construção" dos inteiros.

•Números Figurados: Exploraram padrões geométricos formados por pontos, como os números triangulares (1, 3, 6, 10...), quadrados (1, 4, 9, 16...) e pentagonais, buscando relações entre aritmética e geometria.

•Números Perfeitos: Definiram um número perfeito como aquele que é igual à soma de seus divisores próprios (excluindo ele mesmo). O primeiro número perfeito é 6 (1+2+3=6), seguido por 28 (1+2+4+7+14=28). A busca por números perfeitos fascinou matemáticos por séculos.

•Números Amigáveis: Pares de números onde cada um é a soma dos divisores próprios do outro. O par pitagórico mais conhecido é (220, 284).

•Médias e Proporções: Estudaram diferentes tipos de médias (aritmética, geométrica, harmônica) e suas relações, aplicando-as especialmente à teoria musical.

Essa exploração sistemática das propriedades dos números, buscando padrões, relações e significados ocultos, foi uma marca registrada do pitagorismo e estabeleceu a Teoria dos Números como um ramo fundamental da matemática.

A Crise dos Incomensuráveis: A Descoberta dos Números Irracionais

Paradoxalmente, a busca pitagórica pela ordem numérica perfeita e pela crença de que tudo poderia ser expresso como uma razão de inteiros (números racionais) levou a uma das descobertas mais perturbadoras e revolucionárias da história da matemática: a existência de grandezas incomensuráveis, representadas pelos números irracionais.

A descoberta provavelmente surgiu da aplicação do próprio Teorema de Pitágoras a um simples quadrado de lado 1. A diagonal desse quadrado, pela aplicação do teorema, mede √2 (pois 1² + 1² = d², então d² = 2, e d = √2). Os pitagóricos tentaram expressar √2 como uma fração (uma razão de dois inteiros), mas descobriram, através de uma prova por contradição (reductio ad absurdum), que isso era impossível. √2 não pode ser escrito como p/q, onde p e q são inteiros.

Essa descoberta abalou profundamente os alicerces da filosofia pitagórica. Se nem mesmo a diagonal de um simples quadrado podia ser expressa pela razão de inteiros, como sustentar que "tudo é número" (no sentido de número racional)? A existência de grandezas incomensuráveis representava uma falha na suposta harmonia numérica perfeita do cosmos, um "escândalo lógico".

A tradição associa essa descoberta a Hipaso de Metaponto, um membro da escola. Diz a lenda que Hipaso teria quebrado o voto de segredo pitagórico ao divulgar a existência dos irracionais para o mundo exterior, ou talvez a própria descoberta tenha sido considerada uma heresia. Como punição, relatos variam: alguns dizem que ele foi expulso da escola, outros que foi afogado no mar pelos próprios companheiros pitagóricos durante uma viagem. Embora a veracidade desses relatos seja incerta, eles ilustram o quão chocante e problemática foi a descoberta dos números irracionais para a visão de mundo pitagórica.

Apesar da crise inicial, a descoberta dos irracionais foi um passo crucial no desenvolvimento da matemática, forçando os gregos a repensar a natureza dos números e das grandezas, e eventualmente levando ao desenvolvimento de uma teoria mais robusta das proporções por Eudoxo, que podia lidar tanto com grandezas comensuráveis quanto incomensuráveis.

Pitágoras e a Harmonia do Cosmos: Música, Números e Estrelas

A busca pitagórica pela ordem numérica não se limitava ao mundo abstrato da matemática pura ou às propriedades intrínsecas dos números. Estendia-se à própria estrutura do universo físico, buscando desvendar a harmonia subjacente que regia tanto os sons musicais quanto o movimento dos corpos celestes. Para Pitágoras, o cosmos (kosmos, palavra que ele teria sido o primeiro a usar para designar o universo, significando "ordem" e "beleza") era um sistema perfeitamente ordenado e harmonioso, cujas leis poderiam ser compreendidas através das relações numéricas e musicais.

A Música das Razões: A Escala Pitagórica e o Monocordo

Uma das áreas onde a conexão entre números e fenômenos físicos se manifestou de forma mais clara para os pitagóricos foi na música. A tradição atribui a Pitágoras descobertas fundamentais sobre as relações matemáticas que governam os intervalos musicais consonantes. Diz a lenda que, ao passar por uma oficina de ferreiros, Pitágoras teria notado que martelos de pesos diferentes produziam sons harmoniosos quando golpeavam o metal simultaneamente. Intrigado, ele teria investigado a relação entre os pesos dos martelos e os sons produzidos, descobrindo que os intervalos musicais agradáveis ao ouvido (como a oitava, a quinta e a quarta) correspondiam a razões simples entre os pesos (ou, mais precisamente, entre os comprimentos de cordas vibrantes).

Para investigar essas relações de forma mais sistemática, Pitágoras (ou seus seguidores) teria desenvolvido o monocordo, um instrumento simples consistindo de uma única corda esticada sobre uma caixa de ressonância, com uma ponte móvel que permitia dividir a corda em diferentes comprimentos. Experimentando com o monocordo, eles descobriram que:

•Dividir a corda ao meio (razão 1:2) produzia uma nota uma oitava acima da nota original.

•Dividir a corda em dois terços (razão 2:3) produzia uma nota uma quinta perfeita acima.

•Dividir a corda em três quartos (razão 3:4) produzia uma nota uma quarta perfeita acima.

Essas descobertas foram revolucionárias. Elas demonstravam que a harmonia musical, algo percebido subjetivamente como belo e agradável, possuía uma base matemática objetiva, expressa por razões simples de números inteiros (as mesmas razões encontradas na sagrada tetraktys: 1, 2, 3, 4). A música era, portanto, uma manifestação audível da ordem numérica do universo.

Com base nessas razões fundamentais (2:1, 3:2, 4:3), os pitagóricos construíram uma escala musical, conhecida como escala pitagórica. Essa escala, baseada na sobreposição de quintas perfeitas, dominou a música ocidental por séculos e influenciou profundamente a teoria musical. Embora apresentasse algumas limitações (como a "coma pitagórica", uma pequena discrepância que surge ao completar o ciclo de quintas), ela representou um avanço monumental na compreensão matemática da música e reforçou a convicção pitagórica na onipresença dos números.

A Harmonia das Esferas: A Dança Cósmica dos Planetas

Se a música terrena podia ser explicada por relações numéricas, por que não a música celestial? Estendendo sua visão matemática do som para os céus, os pitagóricos desenvolveram a fascinante doutrina da "Harmonia das Esferas". Eles acreditavam que os planetas, incluindo o Sol e a Lua (considerados planetas na época), moviam-se em órbitas circulares ao redor de um "Fogo Central" (e não da Terra, uma visão surpreendentemente não geocêntrica para a época, embora diferente do heliocentrismo moderno).

Crucialmente, eles postularam que as distâncias entre essas esferas celestes (ou órbitas) e suas velocidades correspondiam às mesmas razões numéricas que governavam os intervalos musicais harmoniosos. Assim como as cordas vibrantes do monocordo produziam sons, os planetas, em seu movimento rápido e regular através do éter celestial, também produziriam um som contínuo e harmonioso – uma música divina e perfeita, a Harmonia das Esferas.

Por que, então, não ouvimos essa música celestial? Os pitagóricos ofereciam algumas explicações. Uma delas era que essa música estava presente desde o nosso nascimento, e por isso nos acostumamos a ela, tornando-nos incapazes de percebê-la conscientemente, assim como o ferreiro não percebe o barulho constante de sua oficina. Outra explicação, mais esotérica, sugeria que apenas almas purificadas, como a do próprio Pitágoras, seriam capazes de ouvir essa harmonia divina.

Embora a ideia de uma música literal produzida pelos planetas tenha sido posteriormente descartada pela ciência, a doutrina da Harmonia das Esferas teve uma influência imensa e duradoura. Ela representou uma das primeiras tentativas de descrever o universo como um sistema unificado, governado por leis matemáticas universais que se aplicam tanto aos céus quanto à Terra. Essa busca por uma ordem matemática no cosmos inspirou astrônomos por séculos, desde Ptolomeu até Johannes Kepler, que, em sua obra Harmonices Mundi (A Harmonia do Mundo), ainda buscava as relações musicais e geométricas que regiam os movimentos planetários, agora dentro de um modelo heliocêntrico. A Harmonia das Esferas permanece como um poderoso símbolo da visão pitagórica de um universo intrinsecamente matemático, ordenado e belo.

O Legado de Pitágoras: Influência Através dos Séculos

A morte de Pitágoras, ocorrida provavelmente em Metaponto por volta de 495 a.C., não significou o fim de suas ideias. Pelo contrário, o pitagorismo continuou a exercer uma influência profunda e multifacetada sobre o pensamento ocidental, reverberando através dos séculos na filosofia, na ciência, na matemática e até mesmo em correntes místicas e esotéricas. Embora a escola original tenha eventualmente se dispersado, as sementes lançadas por Pitágoras e seus seguidores germinaram em diversos campos do conhecimento, moldando a maneira como entendemos o universo e nosso lugar nele.

Impacto na Filosofia: De Platão ao Neoplatonismo

A influência mais direta e significativa do pitagorismo na filosofia grega se deu através de Platão. Embora Platão raramente cite Pitágoras diretamente, muitos dos temas centrais de sua filosofia carregam ecos inconfundíveis do pensamento pitagórico. A distinção platônica entre o mundo sensível (imperfeito e mutável) e o mundo das Ideias ou Formas (eterno, perfeito e acessível apenas pela razão) assemelha-se à ênfase pitagórica na realidade inteligível dos números e das relações matemáticas como mais verdadeiras que a realidade material.

A teoria da reminiscência de Platão, segundo a qual aprender é, na verdade, recordar conhecimentos que a alma possuía antes de encarnar, está claramente ligada à doutrina pitagórica da metempsicose e da imortalidade da alma. A importância que Platão atribui à matemática como propedêutica essencial para a filosofia, evidente na inscrição que supostamente adornava a entrada de sua Academia ("Não entre quem não for geômetra"), reflete diretamente a visão pitagórica da matemática como chave para a compreensão da realidade e purificação da alma. A cosmologia platônica apresentada no diálogo Timeu, que descreve o universo como obra de um Demiurgo que utiliza modelos matemáticos e harmônicos, também demonstra forte influência pitagórica.

Através de Platão, o pitagorismo permeou grande parte da filosofia posterior. Aristóteles, embora crítico de muitos aspectos do platonismo e do pitagorismo (especialmente a ideia de que as coisas são números), dedicou atenção considerável às doutrinas pitagóricas em seus escritos, reconhecendo sua importância histórica e suas contribuições, especialmente na matemática. Mais tarde, durante o período helenístico e romano, o Neopitagorismo surgiu como um renascimento do interesse pelas ideias originais de Pitágoras, enfatizando seus aspectos místicos e religiosos. Figuras como Nicômaco de Gerasa e Jâmblico buscaram reviver os ensinamentos e o modo de vida pitagórico.

Finalmente, o Neoplatonismo, a última grande escola filosófica da antiguidade, fundada por Plotino no século III d.C., integrou fortemente elementos pitagóricos e platônicos. A visão neoplatônica de uma hierarquia da realidade emanando de um Uno transcendente, e a ênfase na contemplação intelectual e na matemática como meios de ascensão da alma, devem muito à tradição pitagórico-platônica.

Influência na Ciência: A Matemática como Linguagem do Universo

A convicção pitagórica de que o universo é fundamentalmente matemático e que suas leis podem ser expressas através de números e geometria teve um impacto duradouro no desenvolvimento da ciência. A busca por uma ordem matemática subjacente aos fenômenos naturais tornou-se um motor poderoso para a investigação científica.

A doutrina da Harmonia das Esferas, como mencionado, inspirou astrônomos por séculos. Johannes Kepler, no século XVII, foi profundamente influenciado pela ideia de uma harmonia matemática nos céus. Embora tenha rejeitado o modelo cosmológico pitagórico original e a ideia de uma música literal, Kepler dedicou anos a encontrar as relações geométricas e harmônicas precisas que governavam as órbitas planetárias (agora elípticas e heliocêntricas), culminando em suas três leis do movimento planetário. Sua obra Harmonices Mundi é um testemunho eloquente da persistência do ideal pitagórico de um cosmos matematicamente ordenado.

Galileu Galilei, outro gigante da Revolução Científica, ecoou a visão pitagórica ao afirmar que o "livro da natureza" está escrito em linguagem matemática. Sua ênfase na quantificação, na medição e na formulação de leis físicas em termos matemáticos representa a concretização do programa pitagórico de compreender o mundo através dos números. A própria física moderna, com suas leis expressas em equações matemáticas complexas, pode ser vista como uma herdeira distante da intuição fundamental de Pitágoras.

O Pitagorismo na Cultura e no Esoterismo

Além da filosofia e da ciência, o legado de Pitágoras também se manifestou em correntes culturais e esotéricas. A aura de mistério que cercava Pitágoras e sua escola, o sigilo, os rituais e a crença na metempsicose, alimentaram lendas e atraíram o interesse de tradições místicas ao longo da história.

A numerologia, a prática de atribuir significados místicos ou divinatórios aos números, embora muitas vezes uma simplificação ou distorção da filosofia pitagórica original, certamente se inspirou na ideia pitagórica de que os números possuem qualidades intrínsecas e simbólicas. Sociedades secretas e ordens esotéricas, como a Maçonaria e os Rosacrucianismo, por vezes reivindicaram uma linhagem espiritual ligada a Pitágoras e às antigas escolas de mistérios, vendo nele um mestre da sabedoria oculta.

Na arte e na arquitetura, a busca pitagórica por proporções harmoniosas (como a Razão Áurea, embora sua conexão direta com os pitagóricos históricos seja debatida) influenciou conceitos de beleza e equilíbrio estético. A ideia de que a harmonia visual e auditiva pode ser baseada em relações matemáticas continua a inspirar artistas, músicos e arquitetos.

Declínio e Dispersão da Escola Pitagórica: O Fim de uma Era

Apesar de sua profunda influência intelectual, a Escola Pitagórica como comunidade organizada e politicamente ativa na Magna Grécia não durou para sempre. O mesmo rigor, exclusividade e envolvimento político que lhe conferiram poder também geraram ressentimento e oposição.

Conflitos Políticos em Crotona e a Revolta Anti-Pitagórica

Os pitagóricos, vindos em grande parte das classes aristocráticas, exerciam considerável influência política em Crotona e outras cidades da Magna Grécia. Essa influência, combinada com o caráter secreto e elitista da escola, começou a gerar atritos com facções democráticas e com aqueles que se sentiam excluídos ou ameaçados pelo poder pitagórico.

Relatos históricos, embora fragmentários e por vezes contraditórios, descrevem um crescente clima de tensão. Uma figura chave nesse conflito parece ter sido Cílon de Crotona, um homem rico e influente que, segundo algumas fontes, teria sido rejeitado como membro da escola e, por vingança ou ambição política, incitou uma revolta popular contra os pitagóricos.

Por volta do final do século VI ou início do século V a.C. (as datas são incertas, podendo ter ocorrido antes ou depois da morte de Pitágoras), essa tensão explodiu em violência. Uma multidão enfurecida teria atacado uma reunião de pitagóricos, incendiando a casa onde estavam congregados e matando muitos deles. Os sobreviventes foram forçados a fugir de Crotona.

Perseguições e a Dispersão Final

Esse evento marcou o início do declínio da influência política direta dos pitagóricos na Magna Grécia. Embora comunidades pitagóricas tenham persistido em outras cidades, como Metaponto e Tarento (onde figuras como Arquitas de Tarento, um renomado matemático, filósofo e estadista pitagórico, floresceram no século IV a.C.), elas enfrentaram perseguições intermitentes.

A escola como uma organização coesa e centralizada gradualmente se desintegrou. Os ensinamentos, antes guardados em segredo, começaram a ser registrados por escrito e a se disseminar mais amplamente, embora talvez de forma fragmentada. Filósofos como Filolau de Crotona (século V a.C.) são creditados por terem sido os primeiros a publicar textos expondo a doutrina pitagórica.

A dispersão dos pitagóricos, embora tenha significado o fim da escola como entidade política e comunitária na Magna Grécia, paradoxalmente contribuiu para a disseminação de suas ideias filosóficas e matemáticas por todo o mundo grego e, eventualmente, para além dele, garantindo a sobrevivência e a contínua influência do legado de Pitágoras.

Conclusão: Pitágoras, o Eterno Arquiteto do Pensamento

Pitágoras de Samos permanece como uma das figuras mais fascinantes e influentes da história intelectual. Mais do que o "pai" de um teorema geométrico, ele foi um arquiteto do pensamento, cujas ideias sobre a natureza fundamentalmente matemática do universo, a importância da harmonia e da ordem, e a busca pela purificação da alma através do conhecimento, ecoaram através dos milênios.

Sua vida, envolta em lendas, simboliza a busca incessante pela sabedoria, integrando conhecimentos de diversas culturas e tradições. Sua escola, uma mistura única de academia científica, comunidade religiosa e força política, representou uma tentativa audaciosa de viver de acordo com princípios filosóficos e de transformar a sociedade através da razão e da virtude.

As contribuições matemáticas atribuídas a ele e seus seguidores – a demonstração do teorema, os avanços na teoria dos números, a descoberta dos irracionais (ainda que problemática para eles) – lançaram as bases para o desenvolvimento da matemática como a conhecemos. Sua visão de um cosmos ordenado por relações numéricas e harmônicas, expressa na música das esferas, inspirou gerações de filósofos e cientistas a buscar as leis matemáticas que regem o universo.

Mesmo o declínio e a dispersão de sua escola não diminuíram o poder de suas ideias. Filtradas através de Platão, Aristóteles, neopitagóricos e neoplatônicos, e redescobertas durante o Renascimento e a Revolução Científica, as intuições fundamentais de Pitágoras sobre a importância dos números e da matemática continuam a ser relevantes.

Ao olharmos para Pitágoras hoje, somos convidados a refletir sobre a profunda conexão entre a matemática, a filosofia, a música, a ciência e a própria busca humana por significado e ordem em um universo vasto e complexo. Ele nos lembra que os números não são apenas ferramentas de cálculo, mas podem ser vistos como uma linguagem universal, capaz de descrever desde a beleza de uma melodia até a majestosa dança dos planetas. O legado de Pitágoras não está apenas nos livros de matemática, mas na própria estrutura do pensamento ocidental, um testemunho duradouro do poder da razão e da busca incessante pela harmonia.