Introdução: A Presença Constante da Vírgula – O Que São Números Decimais?

Em nosso dia a dia, encontramos números que não são inteiros com muita frequência: preços de produtos, medidas de comprimento, resultados de cálculos precisos. Esses números, que possuem uma parte inteira e uma parte fracionária separadas por uma vírgula (em português brasileiro) ou um ponto (em alguns outros sistemas), são os números decimais. Eles são uma forma poderosa e conveniente de representar frações e realizar cálculos com maior precisão.

A beleza dos números decimais reside em sua capacidade de expressar quantidades que estão entre dois números inteiros consecutivos. Nesta postagem abrangente, desvendaremos o mundo dos números decimais, explorando sua estrutura, como lê-los e escrevê-los corretamente, como compará-los e, crucialmente, como realizar as operações básicas com eles. Além disso, veremos como os números decimais se aplicam em diversas situações práticas do nosso cotidiano.

1. A Estrutura dos Números Decimais: Inteiro e Fracionário

Um número decimal é composto por duas partes principais:

• Parte Inteira: Localizada à esquerda da vírgula, representa o número inteiro propriamente dito.

• Parte Decimal: Localizada à direita da vírgula, representa a parte fracionária do número. Cada dígito após a vírgula ocupa uma posição específica, indicando uma fração de uma potência de dez.

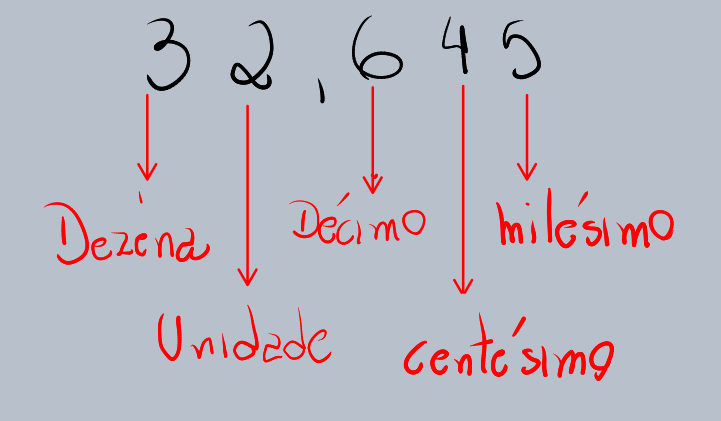
As posições após a vírgula são chamadas de casas decimais:

• Primeira casa decimal: décimos (representa 1/10​)

• Segunda casa decimal: centésimos (representa 1/100​)

• Terceira casa decimal: milésimos (representa 1/1000)

• E assim por diante (décimos de milésimos, centésimos de milésimos, milionésimos...).

Exemplo: No número 3,725:

• 3 é a parte inteira.

• 7 é o dígito dos décimos (7/10).

• 2 é o dígito dos centésimos (2/100).

• 5 é o dígito dos milésimos (5/1000).

Portanto, 3,725 representa 3 + 7/10​+ 2/100​ + 5/1000​.

2. Como Ler Números Decimais: Uma Questão de Posição

Para ler um número decimal corretamente, seguimos algumas regras simples:

1. Lemos a parte inteira normalmente.

2. Lemos a vírgula como "vírgula".

3. Lemos a parte decimal como um número inteiro, seguido da unidade correspondente à última casa decimal.

Exemplos:

• 0,5: Zero vírgula cinco décimos.

• 1,23: Um vírgula vinte e três centésimos.

• 4,07: Quatro vírgula zero sete centésimos.

• 10,008: Dez vírgula zero zero oito milésimos.

• 0,0001: Zero vírgula um décimo de milésimo.

3. Como Escrever Números Decimais: Do Texto à Vírgula

Para escrever um número decimal a partir de sua leitura, fazemos o processo inverso:

1. Escrevemos a parte inteira.

2. Colocamos a vírgula.

3. Escrevemos a parte decimal de forma que o último dígito ocupe a casa decimal indicada. Se necessário, adicionamos zeros à esquerda para posicionar corretamente os dígitos.

Exemplos:

• Três vírgula sete décimos: 3,7

• Quinze vírgula quarenta e cinco centésimos: 15,45

• Dois vírgula zero zero um milésimos: 2,001

• Zero vírgula doze milésimos: 0,012 (note o zero adicionado após a vírgula)

4. Comparação de Números Decimais: Quem é Maior?

Para comparar dois ou mais números decimais, seguimos estes passos:

1. Comparamos as partes inteiras. O número com a maior parte inteira é o maior.

2. Se as partes inteiras forem iguais, comparamos os dígitos na primeira casa decimal (décimos). O número com o maior dígito é o maior.

3. Se os décimos forem iguais, comparamos os dígitos na segunda casa decimal (centésimos), e assim por diante, até encontrarmos dígitos diferentes.

Dica: Para facilitar a comparação, podemos adicionar zeros à direita da parte decimal de um número para que ambos tenham o mesmo número de casas decimais. Isso não altera o valor do número.

Exemplos:

• Comparar 2,5 e 3,1: 3 > 2, então 3,1 é maior.

• Comparar 1,7 e 1,9: As partes inteiras são iguais. Comparando os décimos, 9 > 7, então 1,9 é maior.

• Comparar 0,65 e 0,62: Partes inteiras e décimos são iguais. Comparando os centésimos, 5 > 2, então 0,65 é maior.

• Comparar 4,3 e 4,30: Adicionando um zero, temos 4,30 e 4,30, que são iguais.

5. Operações com Números Decimais: Aritmética com Vírgula

Realizar operações com números decimais segue princípios semelhantes aos dos números inteiros, com atenção especial ao posicionamento da vírgula.

5.1. Adição e Subtração:

Para adicionar ou subtrair números decimais:

1. Alinhamos os números verticalmente, de modo que as vírgulas fiquem umas abaixo das outras. Isso garante que os dígitos com o mesmo valor posicional sejam somados ou subtraídos corretamente.

2. Se necessário, adicionamos zeros à direita para que todos os números tenham o mesmo número de casas decimais.

3. Realizamos a adição ou subtração como se fossem números inteiros.

4. A vírgula no resultado final deve estar alinhada com as vírgulas dos números que foram operados.

Exemplos:

• 2,35 + 1,4 = 2,35 + 1,40 = 3,75

• 5,8 - 2,17 = 5,80 - 2,17 = 3,63

5.2. Multiplicação:

Para multiplicar números decimais:

1. Multiplicamos os números como se fossem inteiros, ignorando as vírgulas inicialmente.

2. Contamos o número total de casas decimais nos fatores (os números que estão sendo multiplicados).

3. No produto final, contamos da direita para a esquerda o mesmo número total de casas decimais e colocamos a vírgula.

Exemplos:

• 1,5 × 2,3 (1 casa decimal + 1 casa decimal = 2 casas decimais no resultado) 15 × 23 = 345 Resultado: 3,45

• 0,12 × 0,4 (2 casas decimais + 1 casa decimal = 3 casas decimais no resultado) 12 × 4 = 48 Resultado: 0,048 (adicionamos um zero à esquerda para ter 3 casas decimais)

5.3. Divisão:

A divisão de números decimais requer um pouco mais de atenção:

1. Se o divisor (o número pelo qual estamos dividindo) for decimal, precisamos transformá-lo em um número inteiro. Fazemos isso multiplicando tanto o divisor quanto o dividendo (o número que está sendo dividido) por uma potência de dez (10, 100, 1000, etc.) que mova a vírgula do divisor para a direita até o final.

2. Realizamos a divisão como se fossem números inteiros.

3. Se durante a divisão precisarmos adicionar zeros ao dividendo para continuar a operação, colocamos uma vírgula no quociente (o resultado da divisão) antes de adicionar o primeiro zero.

Exemplos:

• 7,5 ÷ 2,5 (multiplicamos ambos por 10 para eliminar a vírgula do divisor) 75 ÷ 25 = 3 Resultado: 3

• 12,6 ÷ 0,2 (multiplicamos ambos por 10) 126 ÷ 2 = 63 Resultado: 63

• 5 ÷ 4 (o divisor já é inteiro) 5 ÷ 4 = 1 com resto 1. Adicionamos uma vírgula e um zero ao dividendo (5,0) e continuamos a divisão. 10 ÷ 4 = 2 com resto 2. Adicionamos outro zero (5,00). 20 ÷ 4 = 5 com resto 0. Resultado: 1,25

6. Conversão de Frações em Números Decimais: A Ponte entre as Representações

Todo número racional (que pode ser expresso como uma fração ba​) pode ser representado como um número decimal, que pode ser finito ou infinito e periódico. Para converter uma fração em um decimal, basta dividir o numerador pelo denominador.

Exemplos:

• 1/2 ​= 1÷2 = 0,5 (decimal finito)

• 3/4 ​= 3÷4 = 0,75 (decimal finito)

• 1/3 = 1÷3 = 0,333... (decimal infinito e periódico)

• 7/9 ​= 7÷9 = 0,777... (decimal infinito e periódico)

7. Aplicações Práticas dos Números Decimais: A Matemática do Cotidiano

Os números decimais são ferramentas essenciais em inúmeras situações do nosso dia a dia:

• Comércio e Finanças: Preços de produtos, taxas de juros, cálculos de impostos, conversão de moedas.

• Medições: Comprimento (metros, centímetros), peso (quilogramas, gramas), volume (litros, mililitros).

• Ciências: Resultados de experimentos, constantes físicas (como a gravidade: 9,8 m/s²).

• Tecnologia: Representação de dados em computadores, precisão em cálculos de engenharia.

• Gastronomia: Medidas de ingredientes em receitas.

• Esportes: Tempos de corrida, distâncias percorridas, pontuações.

A familiaridade com os números decimais e a habilidade de operar com eles são fundamentais para a literacia numérica e para a resolução de problemas práticos.

Conclusão: Dominando a Arte da Vírgula Matemática

Os números decimais são uma extensão natural dos números inteiros, permitindo-nos representar quantidades com maior precisão e realizar cálculos de forma eficiente. Compreender sua estrutura, como lê-los, escrevê-los, compará-los e operar com eles é uma habilidade essencial na matemática e em diversas áreas da vida. Espero que este guia completo e didático tenha desvendado os segredos dos números decimais e o capacitado a utilizar a "vírgula matemática" com confiança e clareza. Continue explorando o fascinante mundo dos números!

Algumas video aulas sobre o assunto:

http://www.youtube.com/watch?v=13jlmVyGrLo

Canal: Gis com Giz Matemática

http://www.youtube.com/watch?v=ijhusRH1P7M

Canal: Professora Vilma Ribeiro