Multiplicação e Divisão de frações
Multiplicação e Divisão de Frações: Desvendando os Segredos da Matemática Fracionária
Bem-vindo ao Nossa Matemática! Hoje, vamos mergulhar em um dos tópicos mais fundamentais e, por vezes, desafiadores da matemática: a multiplicação e divisão de frações. Compreender esses conceitos é crucial para qualquer estudante, pois eles são a base para problemas mais complexos e para a aplicação da matemática no dia a dia. Nosso objetivo é desmistificar a multiplicação e divisão de frações, tornando-a acessível, didática e, acima de tudo, fácil de entender. Prepare-se para dominar as frações de uma vez por todas!
O Que São Frações? Uma Breve Revisão
Antes de nos aprofundarmos na multiplicação e divisão de frações, é importante relembrar o que são frações. Para representar uma parte de um todo, usamos uma fração que é formada por um denominador que diz em quantas vezes o todo foi dividido e o numerador que diz a parte que queremos representar do todo. No caso da fração 1/2, por exemplo, o inteiro foi repartido em 2 porções idênticas, e estamos nos referindo a apenas uma dessas porções
Multiplicação de Frações: Multiplicando Partes de um Todo
A multiplicação de frações é um conceito que, à primeira vista, pode parecer contraintuitivo. Ao contrário da multiplicação com números inteiros, que normalmente leva a um resultado maior, a multiplicação de frações pode diminuir o valor. Isso acontece porque, na essência, estamos calculando ‘uma parte de uma parte’.
Como Multiplicar Frações: A Regra Simples
Multiplicar frações é fácil, ,multiplicamos os numeradores para obter o numerador da resposta e depois multiplicamos os denominadores para obter os denominadores da resposta. O resultado será uma nova fração.
Fórmula:
(a/b) * (c/d) = (a * c) / (b * d)
Exemplo Prático:
Vamos multiplicar 1/2 por 3/4. Imagine que você tem 1/2 de uma bolo e quer comer 3/4 dessa parte. Você vai comer uma parte menor.
(1/2) * (3/4) = (1 * 3) / (2 * 4) = 3/8
O resultado é 3/8. Isso significa que você comeu 3 oitavos do bolo original.
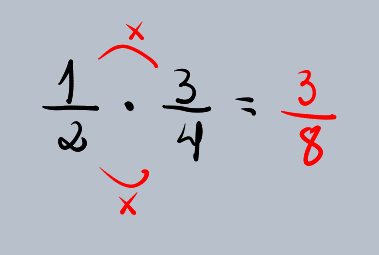
Simplificação na Multiplicação de Frações
Após realizar a multiplicação de frações, é fundamental simplificar o resultado, se possível. Simplificar uma fração significa encontrar um divisor comum entre o numerador e o denominador e então dividi-los. Isso torna a fração mais fácil de entender e de trabalhar.
Exemplo de Simplificação:
Se você multiplicar 2/3 por 3/4:
(2/3) * (3/4) = (2 * 3) / ( 3* 4) = 6/12
Agora, simplificamos 6/12. 6 e 12 podem ser divididos de forma exata por 6. Dividindo ambos por 6, obtemos: 1/2
Então, 6/12 simplificado é 1/2.
Multiplicação de Frações com Números Mistos
Quando você se depara com números mistos (um número inteiro e uma fração, como 1 1/2) na multiplicação de frações, o primeiro passo é convertê-los em frações impróprias. Frações impróprias tem como característica o numerador igual ou maior que o denominador.
Como transformar de misto para fração imprópria:
1.Multiplique o número inteiro pelo denominador da fração.
2.Some o resultado ao numerador.
3.Mantenha o mesmo denominador.
Exemplo: Converter 1 1/2 em fração imprópria.
1.1 * 2 = 2
2.2 + 1 = 3
3.A fração imprópria é 3/2.
Agora é só realizar a multiplicação das frações como já demostrado.
Multiplicação de Frações por um Número Inteiro
Para multiplicar uma fração por um número inteiro, basta transformar o número inteiro em uma fração, colocando-o sobre o denominador 1. Depois efetua a multiplicação normalmente.
Exemplo: Multiplicar 2/5 por 4.
Transforme 4 em 4/1.
(2/5) * (4/1) = (2 * 4) / (5 * 1) = 8/5
Divisão de Frações: Invertendo e Multiplicando
A divisão de frações é outro conceito que pode parecer complicado, mas que se torna muito simples com uma regra fundamental: “manter, trocar, inverter”.
Como Dividir Frações: A Regra do Inverso
Para realizar a divisão de frações, você deve manter a primeira fração, trocar o sinal de divisão por multiplicação e inverter a segunda fração (o numerador vira o denominador e vice-versa). Depois, é só fazer a multiplicação como já visto antes.
Fórmula:
(a/b) ÷ (c/d) = (a/b) * (d/c) = (a * d) / (b * c)
Exemplo Prático:
Vamos dividir 1/2 por 1/4. Imagine que você tem metade de um bolo e quer saber quantos pedaços de 1/4 de bolo você consegue fazer com essa metade.
(1/2) ÷ (1/4)
1.Mantenha a primeira fração: 1/2
2.Mude a conta de dividir para uma conta de multiplicar: *
3.Inverta a segunda fração (1/4 se torna 4/1):
Agora, realize a multiplicação de frações:
(1/2) * (4/1) = (1 * 4) / (2 * 1) = 4/2
Simplificando 4/2, obtemos 2. Isso significa que você consegue fazer 2 pedaços de 1/4 de bolo com metade do bolo.
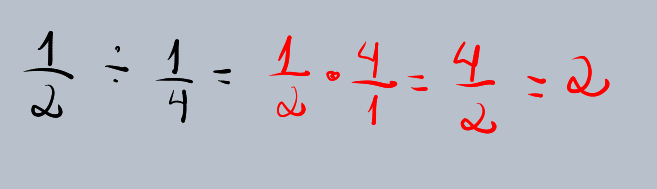
Divisão de Frações com Números Mistos
Assim como na multiplicação, ao lidar com números mistos na divisão de frações, o primeiro passo é convertê-los em frações impróprias. Depois, aplique a regra do “manter, trocar, inverter” e realize a multiplicação e divisão de frações.
Divisão de Frações por um Número Inteiro
Para dividir uma fração por um número inteiro, transforme o número inteiro em uma fração (colocando-o sobre 1). Em seguida, aplique a regra do inverso e realize a multiplicação de frações.
Exemplo: Dividir 3/4 por 2.
Transforme 2 em 2/1.
(3/4) ÷ (2/1)
1.Mantenha a primeira fração: 3/4
2.Substitua o sinal de divisão pelo de multiplicação
3.Inverta a segunda fração (2/1 se torna 1/2):
Agora, realize a multiplicação de frações:
(3/4) * (1/2) = (3 * 1) / (4 * 2) = 3/8
Dicas e Truques para Multiplicação e Divisão de Frações
Dominar a multiplicação e divisão de frações requer prática, mas algumas dicas podem facilitar o processo:
•Simplifique antes de multiplicar: Se possível, simplifique as frações antes de multiplicá-las. Isso pode tornar os números menores e mais fáceis de trabalhar, evitando simplificações maiores no final. Por exemplo, na multiplicação de 2/3 por 3/4, você pode “cortar” o 3 do numerador da primeira fração com o 3 do denominador da segunda fração, e o 2 do numerador da primeira com o 4 do denominador da segunda, resultando em 1/2 diretamente.
•Visualize: Sempre que possível, tente visualizar as frações. Desenhar diagramas ou usar objetos reais pode ajudar a entender o que está acontecendo quando você realiza a multiplicação e divisão de frações.
•Pratique regularmente: A matemática é como um músculo: quanto mais você o exercita, mais forte ele fica. Faça muitos exercícios de multiplicação e divisão de frações para fixar o conhecimento.
A Importância da Multiplicação e Divisão de Frações no Dia a Dia
A multiplicação e divisão de frações não são apenas conceitos abstratos de livros didáticos; elas têm aplicações práticas em diversas situações do nosso cotidiano. Encontramos frações em uma vasta gama de atividades da nossa vida, abrangendo desde a culinária e a construção civil até o mundo das finanças e da pesquisa científica.
Por exemplo, ao dobrar ou reduzir uma receita, você está aplicando a multiplicação de frações. Se uma receita pede 3/4 de xícara de farinha e você quer fazer o dobro, você multiplica 3/4 por 2. Quando você divide uma pizza em fatias iguais para um grupo de amigos, cada fatia representa uma fração do todo.
Perguntas Frequentes sobre Multiplicação e Divisão de Frações
1. Qual a diferença entre multiplicar e dividir frações?
A principal diferença reside na operação e no efeito sobre o resultado. A regra da multiplicação de frações é multiplicar os numeradores e, separadamente, os denominadores. Isso geralmente resulta em uma fração de valor inferior às originais (no caso de frações próprias), pois estamos, na verdade, calculando uma ‘parte de uma parte. Na divisão de frações, você inverte a segunda fração e, em seguida, multiplica. O resultado geralmente é uma fração maior que a primeira (se a segunda fração for própria e menor que 1).
2. A regra para multiplicar ou dividir frações exige que os denominadores sejam iguais, ou isso não é necessário?
Sim! Para somar e subtrair frações, o número de baixo tem que ser igual. Mas para multiplicar e dividir, não tem problema nenhum se os números de baixo forem diferentes. Você pode multiplicar ou dividir diretamente, seguindo as regras que aprendemos.
3. Por que invertemos a segunda fração na divisão?
A estratégia de inverter a segunda fração e então realizar uma multiplicação é um recurso utilizado para transformar um problema de divisão em um de multiplicação com resultado idêntico. Este princípio se baseia na premissa de que a divisão por uma fração é matematicamente idêntica à multiplicação pelo seu recíproco. A título de exemplo, a divisão por 1/2 é análoga à multiplicação por 2. Essa é uma propriedade fundamental da matemática que simplifica a operação.
4. Como sei quando devo simplificar uma fração?
A boa prática matemática diz que você deve simplificar uma fração se o numerador e o denominador compartilharem um divisor comum (diferente de 1). Esse processo facilita a compreensão da fração e é o formato padrão para expressar resultados. É uma boa prática simplificar tanto antes quanto depois de realizar a multiplicação e divisão de frações.
Conclusão: Dominando a Multiplicação e Divisão de Frações
Esperamos que esta explicação detalhada sobre multiplicação e divisão de frações tenha sido útil e esclarecedora. Com as regras simples que você aprendeu aqui e um pouco de dedicação, você estará apto a resolver qualquer problema envolvendo multiplicação e divisão de frações com confiança. Continue explorando o mundo fascinante da matemática com o Nossa Matemática!
