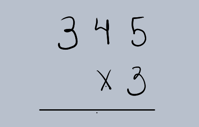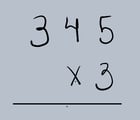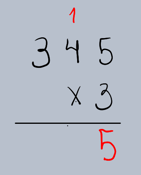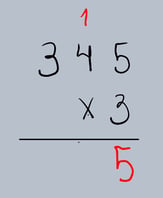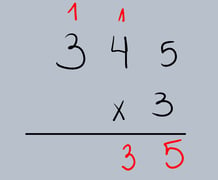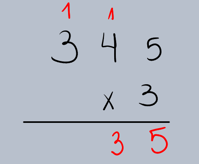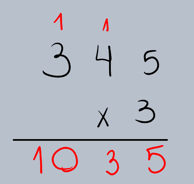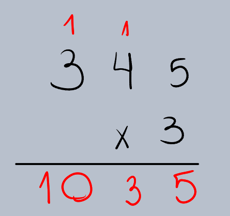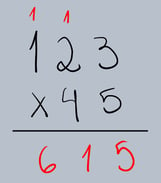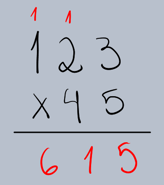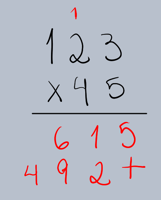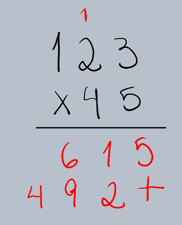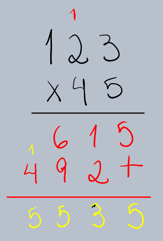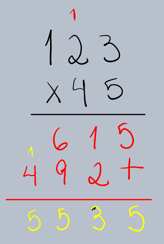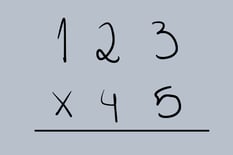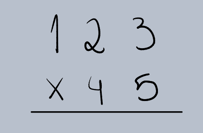Multiplicação: Desvendando o Poder da Adição Repetida no Nossa Matemática

Introdução: O Que é Multiplicação e Por Que Ela é Tão Importante?

Bem-vindo ao Nossa Matemática, o seu portal para desvendar os segredos dos números! Hoje, embarcaremos em uma jornada fascinante para explorar uma das operações fundamentais da matemática: a multiplicação. Mais do que apenas um cálculo, a multiplicação é uma ferramenta poderosa que simplifica a contagem, acelera a resolução de problemas e nos ajuda a compreender o mundo ao nosso redor de uma forma mais eficiente. Se você já se perguntou como calcular rapidamente o total de itens em várias caixas idênticas, ou como determinar o custo total de várias unidades de um produto, a resposta está na multiplicação.

Neste artigo completo e didático, vamos mergulhar fundo no universo da multiplicação, focando exclusivamente em números inteiros. Nosso objetivo é desmistificar essa operação, tornando-a acessível e compreensível para todos, desde estudantes que estão dando os primeiros passos até aqueles que desejam aprimorar seus conhecimentos. Abordaremos a multiplicação de uma forma simples, porém didática, garantindo que você não apenas entenda o "como", mas também o "porquê" por trás de cada cálculo. Prepare-se para uma explicação detalhada, repleta de exemplos práticos, que o guiará passo a passo através do processo da multiplicação, com foco especial na sua interpretação como adição repetida e na visualização prática de seus conceitos.

Multiplicação como Adição Repetida: A Base de Tudo

A maneira mais intuitiva e fundamental de entender a multiplicação é como uma forma abreviada de adição repetida. Imagine que você tem 3 grupos de 4 maçãs. Para saber o total de maçãs, você poderia somar 4 + 4 + 4, o que resulta em 12. A multiplicação nos oferece um caminho mais rápido e elegante para chegar ao mesmo resultado: 3 x 4 = 12. Aqui, o sinal "x" (ou, em alguns contextos, um ponto "." ou um asterisco "*") representa a operação de multiplicação.

Vamos detalhar essa ideia com alguns exemplos:

•Exemplo 1: Grupos de Objetos

•Você tem 5 caixas, e em cada caixa há 6 lápis. Quantos lápis você tem no total?

•Usando a adição repetida: 6 + 6 + 6 + 6 + 6 = 30 lápis.

•Usando a multiplicação: 5 (número de caixas) x 6 (lápis por caixa) = 30 lápis.

•Neste caso, o número 6 (o valor que se repete) é chamado de multiplicando, e o número 5 (quantas vezes o 6 se repete) é o multiplicador. O resultado, 30, é o produto.

•Exemplo 2: Distância Percorrida

•Um carro percorre 8 quilômetros por litro de combustível. Se você usar 4 litros, quantos quilômetros o carro percorrerá?

•Adição repetida: 8 + 8 + 8 + 8 = 32 quilômetros.

•Multiplicação: 4 x 8 = 32 quilômetros.

•Exemplo 3: Contagem de Dinheiro

•Você tem 7 notas de 10 reais. Quanto dinheiro você tem?

•Adição repetida: 10 + 10 + 10 + 10 + 10 + 10 + 10 = 70 reais.

•Multiplicação: 7 x 10 = 70 reais.

Essa interpretação da multiplicação como adição repetida é crucial porque ela conecta a nova operação a algo que já conhecemos e entendemos bem: a adição. Ela nos permite visualizar a multiplicação como a união de grupos iguais, facilitando a compreensão do seu significado e aplicação.

Outras Formas de Visualizar a Multiplicação

Embora a adição repetida seja a base, a multiplicação pode ser visualizada de outras maneiras que enriquecem nossa compreensão e são úteis em diferentes contextos:

1. Arranjos Retangulares (Área)

Imagine que você está organizando cadeiras em um auditório ou ladrilhos em um piso. A multiplicação pode ser usada para calcular o número total de itens em um arranjo retangular. Se você tem 3 fileiras de cadeiras e cada fileira tem 5 cadeiras, o total de cadeiras pode ser visualizado como um retângulo de 3 por 5.

•Visualização: Desenhe um retângulo com 3 linhas e 5 colunas. Conte os quadrados internos. Você verá que há 15 quadrados.

•Cálculo: 3 x 5 = 15 cadeiras.

Essa interpretação é fundamental para entender o conceito de área. A área de um retângulo é calculada multiplicando-se o comprimento pela largura. Por exemplo, um terreno de 10 metros de comprimento por 5 metros de largura tem uma área de 10 x 5 = 50 metros quadrados.

2. Combinações (Princípio Fundamental da Contagem)

A multiplicação também é usada para determinar o número total de combinações possíveis entre diferentes conjuntos de opções. Pense em um restaurante que oferece 3 tipos de pratos principais e 2 tipos de sobremesas.

•Opções de Pratos Principais: Frango, Carne, Peixe

•Opções de Sobremesas: Pudim, Sorvete

Para saber quantas combinações diferentes de refeição (prato principal + sobremesa) você pode fazer, você multiplica o número de opções de pratos principais pelo número de opções de sobremesas:

•Cálculo: 3 (pratos principais) x 2 (sobremesas) = 6 combinações diferentes.

As combinações possíveis seriam:

1.Frango + Pudim

2.Frango + Sorvete

3.Carne + Pudim

4.Carne + Sorvete

5.Peixe + Pudim

6.Peixe + Sorvete

Essa aplicação da multiplicação é a base do Princípio Fundamental da Contagem, amplamente utilizado em probabilidade e estatística.

3. Escala (Aumento ou Diminuição Proporcional)

A multiplicação pode ser vista como uma operação de escala, onde um número é aumentado ou diminuído proporcionalmente. Se você tem uma receita que serve 2 pessoas e precisa adaptá-la para 4 pessoas, você multiplica todos os ingredientes por 2 (o fator de escala).

•Exemplo: Se a receita original pede 1 xícara de farinha para 2 pessoas, para 4 pessoas você precisará de 1 x 2 = 2 xícaras de farinha.

Essa interpretação é comum em diversas áreas, como culinária, engenharia (escalas de projetos) e até mesmo em finanças (cálculo de juros compostos, onde o capital é escalado por um fator de crescimento).

Propriedades Fundamentais da Multiplicação

Assim como a adição, a multiplicação possui propriedades que facilitam os cálculos e nos ajudam a entender melhor como ela funciona. Conhecer essas propriedades é essencial para dominar a multiplicação e aplicá-la de forma eficiente.

1. Propriedade Comutativa

A propriedade comutativa da multiplicação afirma que a ordem dos fatores não altera o produto. Em outras palavras, a x b é sempre igual a b x a.

•Exemplo:

•3 x 5 = 15

•5 x 3 = 15

Essa propriedade é extremamente útil, pois nos permite organizar os números da maneira que for mais conveniente para o cálculo. Se você tem que multiplicar 7 por 100, é mais fácil pensar em 100 x 7 do que 7 x 100, embora o resultado seja o mesmo.

2. Propriedade Associativa

A propriedade associativa da multiplicação nos diz que, ao multiplicar três ou mais números, a forma como agrupamos os fatores não altera o produto. Ou seja, (a x b) x c é igual a a x (b x c).

•Exemplo:

•(2 x 3) x 4 = 6 x 4 = 24

•2 x (3 x 4) = 2 x 12 = 24

Essa propriedade é particularmente útil quando lidamos com multiplicações de vários números, permitindo-nos escolher a ordem de operação que simplifica o cálculo.

3. Propriedade Distributiva

A propriedade distributiva da multiplicação em relação à adição (e à subtração) é uma das mais poderosas e frequentemente utilizadas. Ela estabelece que multiplicar um número pela soma (ou diferença) de outros dois números é o mesmo que multiplicar o número por cada um dos termos da soma (ou diferença) e, em seguida, somar (ou subtrair) os produtos.

•Exemplo (em relação à adição):

•3 x (4 + 2) = 3 x 6 = 18

•(3 x 4) + (3 x 2) = 12 + 6 = 18

•Exemplo (em relação à subtração):

•5 x (7 - 3) = 5 x 4 = 20

•(5 x 7) - (5 x 3) = 35 - 15 = 20

Essa propriedade é fundamental para a álgebra e para a simplificação de expressões matemáticas. Ela nos permite "quebrar" problemas de multiplicação maiores em partes menores e mais gerenciáveis.

4. Elemento Neutro da Multiplicação

O elemento neutro da multiplicação é o número 1. Qualquer número multiplicado por 1 resulta no próprio número.

•Exemplo:

•7 x 1 = 7

•1 x 25 = 25

O número 1 não altera o valor do outro fator na multiplicação, daí o termo "neutro".

5. Elemento Nulo da Multiplicação

O elemento nulo da multiplicação é o número 0. Qualquer número multiplicado por 0 resulta em 0.

•Exemplo:

•9 x 0 = 0

•0 x 123 = 0

Essa propriedade é bastante intuitiva se pensarmos na multiplicação como adição repetida: se você tem 9 grupos de 0 itens, o total de itens é 0. Ou, se você tem 0 grupos de 123 itens, o total também é 0.

O Algoritmo da Multiplicação: Multiplicando Números Maiores

Para multiplicar números inteiros maiores, utilizamos um algoritmo padrão que organiza os cálculos de forma sistemática. Este método é baseado no valor posicional dos dígitos e na propriedade distributiva. Vamos detalhar o processo passo a passo com exemplos claros, que serão acompanhados por imagens para facilitar a visualização.

Multiplicação por um Dígito

Vamos começar com um exemplo simples: 345 x 3.

Passo 1: Armar a Operação

Coloque o multiplicando (o número maior) em cima e o multiplicador (o número menor) embaixo, alinhando as unidades.

Passo 2: Multiplicar as Unidades

Multiplique o dígito das unidades do multiplicando pelo multiplicador. Se o resultado for maior que 9, "suba" a dezena para a próxima coluna.

•5 (unidades de 345) x 3 = 15.

•Escreva o 5 na coluna das unidades e "suba" o 1 (dezena) para a coluna das dezenas.

Passo 3: Multiplicar as Dezenas

Multiplique o dígito das dezenas do multiplicando pelo multiplicador e adicione qualquer valor que tenha "subido" da etapa anterior.

•4 (dezenas de 345) x 3 = 12.

•Adicione o 1 que "subiu": 12 + 1 = 13.

•Escreva o 3 na coluna das dezenas e "suba" o 1 (dezena) para a coluna das centenas.

Passo 4: Multiplicar as Centenas

Multiplique o dígito das centenas do multiplicando pelo multiplicador e adicione qualquer valor que tenha "subido" da etapa anterior.

•3 (centenas de 345) x 3 = 9.

•Adicione o 1 que "subiu": 9 + 1 = 10.

•Escreva o 0 na coluna das centenas e o 1 na coluna dos milhares.

O produto de 345 x 3 é 1035.

Multiplicação por Dois ou Mais Dígitos

Agora, vamos para um exemplo com dois dígitos no multiplicador: 123 x 45.

Passo 1: Armar a Operação

Coloque os números um abaixo do outro, alinhando as unidades.

Passo 2: Multiplicar pelo Dígito das Unidades do Multiplicador

Multiplique o multiplicando (123) pelo dígito das unidades do multiplicador (5), seguindo os mesmos passos da multiplicação por um dígito.

•123 x 5 = 615.

•Escreva o resultado abaixo da linha, alinhado com as unidades.

Passo 3: Multiplicar pelo Dígito das Dezenas do Multiplicador

Multiplique o multiplicando (123) pelo dígito das dezenas do multiplicador (4). Lembre-se que o 4 está na casa das dezenas, então seu valor é 40. Por isso, o resultado dessa multiplicação deve começar na coluna das dezenas (ou seja, adicione um zero à direita ou desloque o resultado uma casa para a esquerda).

•123 x 4 = 492.

•Escreva o resultado 492 abaixo do 615, mas deslocado uma casa para a esquerda (ou adicione um zero no final, transformando em 4920).

Passo 4: Somar os Produtos Parciais

Agora, some os resultados das multiplicações parciais.

O produto de 123 x 45 é 5535.

Multiplicação com Números Inteiros (Positivos e Negativos)

Até agora, focamos em números naturais (inteiros positivos e zero). No entanto, a multiplicação também se aplica a números inteiros negativos. As regras para os sinais são simples e cruciais:

1.Positivo x Positivo = Positivo: Quando multiplicamos dois números positivos, o resultado é positivo.

•Exemplo: 3 x 4 = 12

2.Negativo x Negativo = Positivo: Quando multiplicamos dois números negativos, o resultado é positivo.

•Exemplo: (-3) x (-4) = 12

•Por que isso acontece? Pense em "tirar uma dívida". Se você "tira" (multiplica por negativo) 3 dívidas de 4 reais cada, o resultado é que você fica com 12 reais a mais (positivo).

3.Positivo x Negativo = Negativo: Quando multiplicamos um número positivo por um negativo (ou vice-versa), o resultado é negativo.

•Exemplo: 3 x (-4) = -12

•Exemplo: (-3) x 4 = -12

•Por que isso acontece? Pense em "adicionar uma dívida". Se você "adiciona" (multiplica por positivo) 3 dívidas de 4 reais cada, o resultado é que você fica com 12 reais a menos (negativo).

Em resumo, a regra dos sinais é:

•Sinais iguais (ambos positivos ou ambos negativos) = Produto positivo.

•Sinais diferentes (um positivo e um negativo) = Produto negativo.

Aplicações Práticas da Multiplicação no Cotidiano

A multiplicação não é apenas um conceito abstrato de sala de aula; ela está presente em diversas situações do nosso dia a dia. Compreender suas aplicações nos ajuda a valorizar sua importância e a utilizá-la de forma eficaz.

•Compras e Finanças:

•Calcular o custo total de vários itens iguais (ex: 5 camisetas a R30cada=5x30=R 30 cada = 5 x 30 = R30cada=5x30=R 150).

•Determinar o valor total de parcelas (ex: 12 parcelas de R250=12x250=R 250 = 12 x 250 = R250=12x250=R 3000).

•Calcular juros simples ou compostos (embora estes envolvam conceitos mais avançados, a multiplicação é a base).

•Culinária e Receitas:

•Aumentar ou diminuir as quantidades de ingredientes em uma receita para servir mais ou menos pessoas.

•Calcular o tempo total de preparo se cada etapa leva um certo tempo.

•Viagens e Distâncias:

•Estimar a distância total percorrida em uma viagem, sabendo a velocidade média e o tempo (Distância = Velocidade x Tempo).

•Calcular o consumo de combustível (Litros consumidos = Distância / Quilômetros por litro).

•Construção e Design:

•Calcular a área de um cômodo para determinar a quantidade de piso ou tinta necessária.

•Dimensionar materiais (ex: número de tijolos para uma parede).

•Organização e Logística:

•Contar o número total de itens em caixas ou pacotes.

•Planejar a capacidade de armazenamento.

•Esportes e Jogos:

•Calcular pontuações em jogos que envolvem múltiplos pontos por ação.

•Determinar o número de combinações possíveis em jogos de tabuleiro ou cartas.

Esses são apenas alguns exemplos de como a multiplicação é uma ferramenta indispensável em nosso cotidiano, facilitando cálculos e auxiliando na tomada de decisões.

Estratégias de Cálculo Mental para Multiplicação

Desenvolver habilidades de cálculo mental é extremamente útil para agilizar a resolução de problemas e fortalecer a compreensão numérica. Aqui estão algumas estratégias para multiplicar mentalmente:

1. Decomposição de Números

Decomponha um dos fatores em partes mais fáceis de multiplicar. Use a propriedade distributiva.

•Exemplo: 15 x 6

•Pense em 15 como 10 + 5.

•(10 x 6) + (5 x 6) = 60 + 30 = 90.

•Exemplo: 23 x 4

•Pense em 23 como 20 + 3.

•(20 x 4) + (3 x 4) = 80 + 12 = 92.

2. Dobrar e Reduzir pela Metade

Se um dos fatores for par, você pode dobrar um e reduzir o outro pela metade para simplificar a multiplicação.

•Exemplo: 16 x 5

•Reduza 16 pela metade (8) e dobre 5 (10).

•8 x 10 = 80.

•Exemplo: 14 x 8

•Reduza 14 pela metade (7) e dobre 8 (16).

•7 x 16 (agora você pode decompor 16 em 10 + 6) = (7 x 10) + (7 x 6) = 70 + 42 = 112.

3. Multiplicação por 10, 100, 1000...

Multiplicar por potências de 10 é muito simples: basta adicionar o número de zeros do fator 10, 100, 1000, etc., ao final do outro número.

•Exemplo: 25 x 10 = 250 (adicione um zero)

•Exemplo: 12 x 100 = 1200 (adicione dois zeros)

•Exemplo: 7 x 1000 = 7000 (adicione três zeros)

4. Usando Números Próximos a 10, 100, etc.

Se um dos fatores estiver próximo de uma potência de 10, você pode usar a propriedade distributiva para facilitar.

•Exemplo: 8 x 9

•Pense em 9 como (10 - 1).

•8 x (10 - 1) = (8 x 10) - (8 x 1) = 80 - 8 = 72.

•Exemplo: 15 x 99

•Pense em 99 como (100 - 1).

•15 x (100 - 1) = (15 x 100) - (15 x 1) = 1500 - 15 = 1485.

Praticar essas estratégias regularmente pode melhorar significativamente sua agilidade no cálculo mental e sua compreensão da multiplicação.

Relação da Multiplicação com Outras Operações

A matemática é um campo interconectado, e a multiplicação não existe isoladamente. Ela possui relações intrínsecas com a adição, a subtração e, especialmente, com a divisão.

Multiplicação e Adição

Como já vimos, a multiplicação é essencialmente uma adição repetida. Essa é a relação mais direta e fundamental. Entender essa conexão é o primeiro passo para dominar a multiplicação.

Multiplicação e Subtração

A relação com a subtração é mais indireta, mas existe através da propriedade distributiva. Por exemplo, 5 x (7 - 3) pode ser resolvido como (5 x 7) - (5 x 3), o que envolve subtrações.

Multiplicação e Divisão: Operações Inversas

A relação mais importante da multiplicação com outra operação é com a divisão. A divisão é a operação inversa da multiplicação. Se você sabe que 3 x 4 = 12, então você também sabe que 12 dividido por 3 é 4, e 12 dividido por 4 é 3.

•Exemplo:

•Se 6 x 7 = 42,

•Então 42 ÷ 6 = 7

•E 42 ÷ 7 = 6

Essa relação é crucial para a resolução de equações e para a compreensão de problemas que envolvem a distribuição ou o agrupamento de quantidades. Se você tem um produto e um dos fatores, a divisão permite encontrar o fator desconhecido.

Conclusão: Multiplicação, Uma Habilidade Essencial

Chegamos ao fim da nossa exploração aprofundada sobre a multiplicação de números inteiros. Esperamos que este artigo tenha desvendado os mistérios dessa operação fundamental, mostrando que ela é muito mais do que apenas memorizar a tabuada. A multiplicação é uma linguagem universal que nos permite quantificar, comparar e resolver problemas de forma eficiente em diversas áreas da vida.

Revisitamos a multiplicação como adição repetida, exploramos suas visualizações como arranjos retangulares e combinações, e mergulhamos nas suas propriedades essenciais: comutativa, associativa, distributiva, elemento neutro e elemento nulo. Além disso, detalhamos o algoritmo passo a passo para multiplicar números maiores e compreendemos as regras dos sinais para números inteiros positivos e negativos. As aplicações práticas no cotidiano e as estratégias de cálculo mental reforçam a relevância dessa habilidade.

Dominar a multiplicação é um passo crucial em sua jornada matemática. Ela serve como alicerce para conceitos mais avançados, como frações, decimais, álgebra e cálculo. A prática constante é a chave para a fluência. Continue explorando, questionando e aplicando o que aprendeu. O "Nossa Matemática" está aqui para apoiá-lo em cada etapa do caminho. Continue praticando e desvendando o poder dos números!

Multiplicação e a Tabuada: Ferramenta Essencial para a Fluência

A tabuada é, sem dúvida, uma das ferramentas mais importantes no aprendizado da multiplicação. Ela é uma tabela que lista os produtos da multiplicação de um número por outros números inteiros, geralmente de 1 a 10. Dominar a tabuada de cor é fundamental para agilizar os cálculos e construir uma base sólida para conceitos matemáticos mais complexos.

Como a Tabuada Ajuda?

1.Agilidade no Cálculo: Ao invés de realizar a adição repetida ou o algoritmo completo para cada multiplicação simples, a tabuada permite que você acesse o resultado instantaneamente.

2.Base para Cálculos Maiores: A tabuada é a base para a multiplicação de números maiores. Como vimos no algoritmo, multiplicamos dígito por dígito, e esses produtos parciais vêm diretamente da tabuada.

3.Compreensão de Padrões: Ao estudar a tabuada, você começa a perceber padrões e relações entre os números, o que aprofunda sua compreensão numérica.

4.Confiança: Saber a tabuada de cor aumenta a confiança do estudante em suas habilidades matemáticas.

Dicas para Memorizar a Tabuada:

•Comece pelas mais fáceis: As tabuadas do 0, 1, 10 e 5 são geralmente as mais fáceis de memorizar. Comece por elas para construir confiança.

•Tabuada do 0: Qualquer número multiplicado por 0 é 0.

•Tabuada do 1: Qualquer número multiplicado por 1 é ele mesmo.

•Tabuada do 10: Basta adicionar um zero ao número.

•Tabuada do 5: Os resultados sempre terminam em 0 ou 5.

•Use a Propriedade Comutativa: Lembre-se que 3 x 7 é o mesmo que 7 x 3. Se você sabe um, sabe o outro!

•Padrões e Truques:

•Tabuada do 9: Os resultados da tabuada do 9 têm uma soma de dígitos igual a 9 (ex: 9x2=18, 1+8=9; 9x3=27, 2+7=9). Além disso, os dígitos das dezenas aumentam e os das unidades diminuem.

•Tabuada do 2: É o dobro do número.

•Tabuada do 4: É o dobro do dobro do número.

•Prática Regular: A memorização vem com a repetição. Use cartões de memória, jogos, aplicativos ou simplesmente pratique com frequência.

•Visualização: Desenhe arranjos retangulares ou grupos de objetos para visualizar os produtos.

Multiplicação na Linha Numérica: Uma Perspectiva Visual

Outra forma de visualizar a multiplicação, especialmente para iniciantes, é usando a linha numérica. Embora seja mais prática para números menores, ela reforça a ideia da multiplicação como saltos de tamanhos iguais.

•Exemplo: 3 x 4

•Comece no 0 na linha numérica.

•Dê 3 saltos, cada um de 4 unidades.

•Primeiro salto: 0 para 4.

•Segundo salto: 4 para 8.

•Terceiro salto: 8 para 12.

•Você chegará ao 12, que é o produto.

Essa visualização é particularmente útil para entender a multiplicação como uma série de incrementos iguais, conectando-a diretamente à adição repetida de uma forma espacial.

Multiplicação por Decomposição em Fatores Primos: Uma Abordagem Avançada

Para números maiores, ou para entender a estrutura dos números, a multiplicação pode ser facilitada pela decomposição em fatores primos. Embora não seja um método de cálculo direto para o dia a dia, é fundamental para a compreensão de conceitos como Mínimo Múltiplo Comum (MMC) e Máximo Divisor Comum (MDC).

•Exemplo: 12 x 15

•Decomponha 12 em fatores primos: 2 x 2 x 3

•Decomponha 15 em fatores primos: 3 x 5

•Agora, multiplique todos os fatores primos juntos: (2 x 2 x 3) x (3 x 5) = 2 x 2 x 3 x 3 x 5

•Reagrupe para facilitar: (2 x 2) x (3 x 3) x 5 = 4 x 9 x 5 = 36 x 5 = 180.

Este método demonstra a natureza fundamental da multiplicação como a combinação de fatores, e como a ordem desses fatores não importa (propriedade comutativa e associativa).

Erros Comuns na Multiplicação e Como Evitá-los

Mesmo com uma compreensão sólida, alguns erros são comuns ao realizar multiplicações. Estar ciente deles pode ajudar a evitá-los.

1.Erro de Alinhamento: Ao multiplicar números com múltiplos dígitos, o alinhamento incorreto dos produtos parciais é um erro frequente. Lembre-se de que cada produto parcial deve ser deslocado uma casa para a esquerda em relação ao dígito do multiplicador que o gerou.

2.Esquecer de "Subir" os Números: Na multiplicação, quando o produto de dois dígitos excede 9, a dezena deve ser "subida" para a próxima coluna. Esquecer de fazer isso ou de adicioná-la no próximo passo é um erro comum.

3.Erro na Tabuada: A falta de memorização da tabuada pode levar a erros básicos nos produtos de um único dígito, que se propagam para o resultado final.

4.Erro de Sinal: Ao multiplicar números inteiros (positivos e negativos), confundir as regras dos sinais é um erro frequente. Lembre-se: sinais iguais, resultado positivo; sinais diferentes, resultado negativo.

5.Pressa: A pressa pode levar a erros de desatenção. É importante realizar os cálculos com calma e revisar cada etapa.

Para evitar esses erros, a prática é fundamental. Além disso, sempre revise seus cálculos, especialmente em problemas mais complexos. Uma boa estratégia é refazer o cálculo de uma maneira diferente, se possível, para verificar a consistência dos resultados.

Multiplicação e o Conceito de Fatoração

A multiplicação está intrinsecamente ligada ao conceito de fatoração. Fatorar um número significa expressá-lo como um produto de seus fatores. Por exemplo, os fatores de 12 são 1, 2, 3, 4, 6 e 12, pois 1 x 12 = 12, 2 x 6 = 12 e 3 x 4 = 12.

Fatores e Múltiplos

•Fatores: São os números que, quando multiplicados, resultam em um determinado produto. No exemplo 3 x 4 = 12, 3 e 4 são fatores de 12.

•Múltiplos: São os resultados da multiplicação de um número por qualquer número inteiro. Os múltiplos de 3 são 3, 6, 9, 12, 15, etc. (3x1, 3x2, 3x3, 3x4, 3x5...).

Compreender a relação entre fatores e múltiplos é crucial para a divisão, para a simplificação de frações e para a resolução de problemas que envolvem padrões numéricos.

Multiplicação e a Propriedade Zero do Produto

A propriedade zero do produto é uma consequência direta do elemento nulo da multiplicação. Ela afirma que se o produto de dois ou mais fatores é zero, então pelo menos um dos fatores deve ser zero.

•Exemplo: Se a x b = 0, então a = 0 ou b = 0 (ou ambos).

Essa propriedade é fundamental na resolução de equações algébricas, onde ela é usada para encontrar as raízes de uma equação polinomial.

A Importância da Multiplicação na Ciência e Tecnologia

A multiplicação é a espinha dorsal de inúmeras aplicações na ciência e tecnologia. Desde a física até a computação, sua presença é onipresente.

•Física: Cálculos de força (Força = Massa x Aceleração), energia, trabalho, e muitos outros conceitos físicos dependem da multiplicação.

•Engenharia: No dimensionamento de estruturas, cálculo de cargas, projeto de circuitos elétricos, a multiplicação é constantemente utilizada.

•Computação: Os computadores realizam bilhões de operações de multiplicação por segundo. Algoritmos de criptografia, processamento de imagens, gráficos 3D e inteligência artificial dependem fortemente de operações de multiplicação.

•Economia e Finanças: Modelos econômicos, projeções financeiras, cálculo de juros, inflação e crescimento populacional utilizam a multiplicação como base.

•Estatística e Probabilidade: O cálculo de probabilidades, combinações e permutações, e a análise de dados estatísticos frequentemente envolvem a multiplicação.

Essa vasta gama de aplicações demonstra que a multiplicação não é apenas uma operação matemática, mas uma ferramenta essencial para a compreensão e manipulação do mundo quantitativo.

Multiplicação e a Construção do Pensamento Lógico

Além de suas aplicações práticas, o estudo da multiplicação contribui significativamente para o desenvolvimento do pensamento lógico e do raciocínio abstrato. Ao aprender a multiplicar, os estudantes são desafiados a:

•Identificar Padrões: A tabuada e as propriedades da multiplicação revelam padrões numéricos que estimulam a observação e a generalização.

•Resolver Problemas: A multiplicação fornece uma estrutura para abordar e resolver problemas complexos, exigindo a aplicação de estratégias e a tomada de decisões.

•Pensamento Abstrato: A capacidade de entender a multiplicação como uma operação que transcende a simples adição repetida, aplicando-a a conceitos como área e combinações, desenvolve o pensamento abstrato.

•Conexões Matemáticas: A multiplicação serve como uma ponte para outras áreas da matemática, como a álgebra e a geometria, fortalecendo a compreensão de como os conceitos matemáticos se interligam.

Em suma, a multiplicação é uma porta de entrada para um universo de conhecimento matemático, capacitando os indivíduos a pensar de forma mais crítica e analítica.

O Futuro da Multiplicação: Além dos Números Inteiros

Embora este artigo tenha focado exclusivamente na multiplicação de números inteiros, é importante notar que o conceito se estende a outros conjuntos numéricos, cada um com suas particularidades e aplicações:

•Números Decimais: A multiplicação de decimais envolve as mesmas regras básicas, mas com atenção especial à posição da vírgula no produto.

•Frações: A multiplicação de frações é realizada multiplicando-se os numeradores entre si e os denominadores entre si.

•Números Racionais: Incluem inteiros, decimais e frações, e a multiplicação segue as regras gerais.

•Números Reais: Abrangem todos os números racionais e irracionais, e a multiplicação mantém suas propriedades.

•Números Complexos: Introduzem uma nova dimensão à multiplicação, com regras específicas para a parte imaginária.

Cada um desses conjuntos numéricos expande o poder e a aplicabilidade da multiplicação, tornando-a uma operação verdadeiramente universal na matemática.

Multiplicação e a História da Matemática

A multiplicação, em suas diversas formas, tem uma história rica e fascinante que remonta às civilizações antigas. Desde os métodos de contagem primitivos até os algoritmos complexos de hoje, a evolução da multiplicação reflete o desenvolvimento do pensamento humano.

•Antigo Egito: Os egípcios utilizavam um método de duplicação e adição para realizar multiplicações, que se assemelhava à adição repetida.

•Babilônios: Desenvolveram tabelas de multiplicação baseadas em seu sistema numérico de base 60.

•Gregos: Embora focados na geometria, os gregos também contribuíram para o entendimento teórico da multiplicação.

•Índia e o Sistema Decimal: A introdução do sistema de numeração decimal e o conceito de zero na Índia revolucionaram a forma como os cálculos, incluindo a multiplicação, eram realizados, tornando-os muito mais eficientes.

•Árabes: Foram os responsáveis por difundir o sistema de numeração indiano e os algoritmos de cálculo para o Ocidente, incluindo o algoritmo da multiplicação que usamos hoje.

•Renascimento Europeu: Com o avanço do comércio e da ciência, a necessidade de cálculos mais rápidos e precisos impulsionou o desenvolvimento de novos métodos e ferramentas para a multiplicação, culminando na formalização dos algoritmos modernos.

Essa breve retrospectiva histórica nos mostra que a multiplicação não é uma invenção recente, mas o resultado de milênios de engenhosidade humana, adaptando-se e evoluindo para atender às crescentes demandas da sociedade.

fator 10, 100, 1000, etc., ao final do outro número.