Multiplicação de Inteiros
Multiplicação: Desvendando o Poder da Adição Repetida no Nossa Matemática
Bem-vindo ao Nossa Matemática, o seu portal para desvendar os segredos dos números! Hoje, vamos em uma aventura para explorar uma das operações mais importantes da matemática: a multiplicação. Mais do que apenas um cálculo, a multiplicação é uma ferramenta poderosa que simplifica a contagem, acelera a resolução de problemas e nos ajuda a compreender o mundo ao nosso redor de uma forma mais eficiente. Se você já se perguntou como calcular rapidamente o total de itens em várias caixas idênticas, ou como determinar o custo total de várias unidades de um produto, a resposta está na multiplicação.
Neste artigo completo criado por Nossa Matemática, vamos nos aprofundar no estudo da multiplicação, nos especializando nos números inteiros. Nosso objetivo é desmistificar essa operação, tornando-a acessível e compreensível para todos, desde estudantes que estão dando os primeiros passos até aqueles que desejam aprimorar seus conhecimentos. Abordaremos a multiplicação de uma forma simples, porém didática, garantindo que você não apenas entenda o “como”, mas também o “porquê” por trás de cada cálculo. Prepare-se para uma explicação detalhada, repleta de exemplos práticos, que o guiará passo a passo através do processo da multiplicação, com foco especial na sua interpretação como adição repetida e na visualização prática de seus conceitos.
Multiplicação como Adição Repetida: A Base de Tudo
A melhor maneira de se interpretar a multiplicação é como uma forma de se representar somas sucessivas. Imagine que você tem 3 grupos de 4 maçãs. Para saber o total de maçãs, você poderia somar 4 + 4 + 4, o que resulta em 12. A multiplicação nos oferece um caminho mais rápido e elegante para chegar ao mesmo resultado: 3 x 4 = 12. Aqui, o sinal “x” (ou, em alguns contextos, um ponto “.” ou um asterisco “*”) representa a operação de multiplicação.
Vamos detalhar essa ideia com alguns exemplos:
•Exemplo 1: Grupos de Objetos
•Você tem 5 estojos, e em cada caixa há 6 canetas. Quantas canetas você tem no total?
•Usando a adição repetida: 6 + 6 + 6 + 6 + 6 = 30 canetas.
•Usando a multiplicação: 5 (número de estojos) x 6 (canetas por estojo) = 30 canetas.
•No exemplo, o número 6 é chamado de multiplicando, e o número 5 é o multiplicador. O resultado, 30, é o produto.
•Exemplo 2: Distância Percorrida
•Um carro percorre 8 quilômetros por litro de combustível. Se você usar 4 litros, quantos quilômetros o carro percorrerá?
•Adição repetida: 8 + 8 + 8 + 8 = 32 quilômetros.
•Multiplicação: 4 x 8 = 32 quilômetros.
•Exemplo 3: Contagem de Dinheiro
•Você tem 7 notas de 10 reais. Quanto dinheiro você tem?
•Adição repetida: 10 + 10 + 10 + 10 + 10 + 10 + 10 = 70 reais.
•Multiplicação: 7 x 10 = 70 reais.
Este pensamento a respeito da multiplicação como uma soma de fatores sucessivos é muito importante, pois, nos trás de volta a uma operação que já conhecemos: a adição. Esta ideia nos ajuda a ver a multiplicação como a soma de grupos iguais, ajudando na fixação do conteúdo.
Outras Formas de Visualizar a Multiplicação
Embora a adição repetida seja a base, a multiplicação pode ser visualizada de outras maneiras que enriquecem nossa compreensão e são úteis em diferentes contextos:
1. Arranjos Retangulares (Área)
Imagine que você está organizando cadeiras em um auditório ou ladrilhos em um piso. A multiplicação também pode ser vista no cálculo do número total de itens em um arranjo simples. Se você tem 3 fileiras de cadeiras e cada fileira tem 5 cadeiras, o total de cadeiras pode ser visualizado como um retângulo de 3 por 5.
•Visualização: Desenhe um retângulo com 3 linhas e 5 colunas. Conte os quadrados internos. Você verá que há 15 quadrados.
•Cálculo: 3 x 5 = 15 cadeiras.
Essa ideia é primordial para compreender o pensamento do cálculo de área. A área de um retângulo é calculada multiplicando o comprimento pela largura. Por exemplo, um terreno de 10 metros de comprimento por 5 metros de largura tem uma área de 10 x 5 = 50 metros quadrados.
2. Combinações (Princípio Fundamental da Contagem)
A multiplicação também é usada para determinar o número total de combinações possíveis entre diferentes conjuntos de opções. Considere um restaurante que disponibiliza 3 opções de pratos principais e 2 opções de sobremesas.
•Opções de Pratos Principais: Frango, Carne, Peixe
•Opções de Sobremesas: Pudim, Sorvete
Para descobrir quantas combinações distintas de refeição (prato principal e sobremesa) são possíveis, basta multiplicar a quantidade de opções de pratos principais pela quantidade de opções de sobremesas.
Cálculo: 3 opções de pratos principais vezes 2 opções de sobremesas resultam em 6 combinações distintas.
As combinações possíveis seriam:
1.Frango + Pudim
2.Frango + Sorvete
3.Carne + Pudim
4.Carne + Sorvete
5.Peixe + Pudim
6.Peixe + Sorvete
Essa aplicação da multiplicação é a base do Princípio Fundamental da Contagem, amplamente utilizado em probabilidade e estatística.
3. Escala (Aumento ou Diminuição Proporcional)
A multiplicação pode ser vista como uma operação de escala, onde um número é aumentado ou diminuído proporcionalmente. Se você tem uma receita que serve 2 pessoas e precisa adaptá-la para 4 pessoas, você multiplica todos os ingredientes por 2 (o fator de escala).
•Exemplo: Se a receita original pede 1 xícara de farinha para 2 pessoas, para 4 pessoas você precisará de 1 x 2 = 2 xícaras de farinha.
Essa interpretação é comum em diversas áreas, como culinária, engenharia (escalas de projetos) e até mesmo em finanças (cálculo de juros compostos, onde o capital é escalado por um fator de crescimento).
Propriedades Fundamentais da Multiplicação
Assim como a adição, a multiplicação possui propriedades que facilitam os cálculos e nos ajudam a entender melhor como ela funciona. Conhecer essas propriedades é essencial para dominar a multiplicação e aplicá-la de forma eficiente.
1. Propriedade Comutativa
A propriedade comutativa da multiplicação estabelece que a ordem em que os fatores são multiplicados não afeta o resultado final. Em outras palavras, a x b é sempre igual a b x a.
•Exemplo:
•3 x 5 = 15
•5 x 3 = 15
Essa propriedade é extremamente útil, pois nos permite organizar os números da maneira que for mais conveniente para o cálculo. Se você tem que multiplicar 7 por 100, é mais fácil pensar em 100 x 7 do que 7 x 100, embora o resultado seja o mesmo.
2. Propriedade Associativa
A ordem em que os fatores são agrupados não altera o produto final. Assim, multiplicar (a x b) por c resulta no mesmo que multiplicar a por (b x c).
•(2 x 3) x 4 = 6 x 4 = 24
Ao multiplicar 2 pelo resultado de (3 x 4), obtemos 2 x 12, que é igual a 24.
Essa propriedade é particularmente útil quando lidamos com multiplicações de vários números, permitindo-nos escolher a ordem de operação que simplifica o cálculo.
3. Propriedade Distributiva
A propriedade distributiva da multiplicação em relação à adição (e à subtração) é uma das mais poderosas e frequentemente utilizadas. Multiplicar um número pela soma (ou diferença) de outros dois é equivalente a multiplicar o número por cada um dos termos separadamente
•Exemplo (em relação à adição):
•Ao calcular 3 x (4 + 2), a regra de ordem das operações exige que a soma no parêntese seja feita primeiro, resultando em 3 x 6. Por fim, a multiplicação resulta em 18
•(3 x 4) + (3 x 2) = 12 + 6 = 18
•Exemplo (em relação à subtração):
•Primeiro, resolvemos a operação dentro dos parênteses, subtraindo 3 de 7, o que resulta em 4. Em seguida, multiplicamos 5 por 4, chegando ao resultado final de 20.
•(5 x 7) – (5 x 3) = 35 – 15 = 20
Essa propriedade é fundamental para a álgebra e para a simplificação de expressões matemáticas. Ela nos permite “quebrar” problemas de multiplicação maiores em partes menores e mais gerenciáveis.
4. Elemento Neutro da Multiplicação
A característica do número 1 de não alterar o resultado de uma multiplicação faz dele o elemento neutro.
o •Exemplo:
•7 x 1 = 7
•1 x 25 = 25
O termo ‘neutro’ é usado porque o número 1 não afeta o resultado do outro fator na multiplicação
5. Elemento Nulo da Multiplicação
O número 0 é o elemento nulo da multiplicação, pois qualquer número multiplicado por ele sempre resultará em zero
•Exemplo:
•9 x 0 = 0
•0 x 123 = 0
propriedade se torna intuitiva quando vemos a multiplicação como uma soma de parcelas iguais: ter 9 grupos com 0 itens em cada um resulta em um total de 0 itens
O Algoritmo da Multiplicação: Multiplicando Números Maiores
Para multiplicar números inteiros maiores, utilizamos um algoritmo padrão que organiza os cálculos de forma sistemática. Este método é baseado no valor posicional dos dígitos e na propriedade distributiva. Vamos detalhar o processo passo a passo com exemplos claros, que serão acompanhados por imagens para facilitar a visualização.
Multiplicação por um Dígito
Comecemos com um exemplo básico: 345 x 3
Passo 1: Armar a Operação
Coloque o multiplicando (o número maior) em cima e o multiplicador (o número menor) embaixo, alinhando as unidades
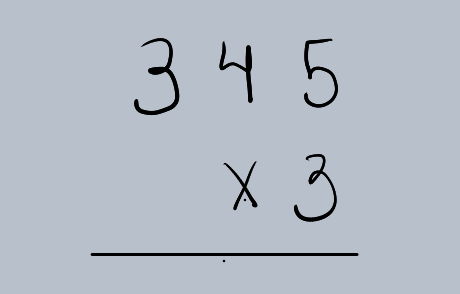
Passo 2: Multiplicar as Unidades
Multiplique o dígito das unidades do multiplicando pelo multiplicador. Se o resultado for maior que 9, “suba” a dezena para a próxima coluna.
•5 (unidades de 345) x 3 = 15.
•Escreva o 5 na coluna das unidades e “suba” o 1 (dezena) para a coluna das dezenas.
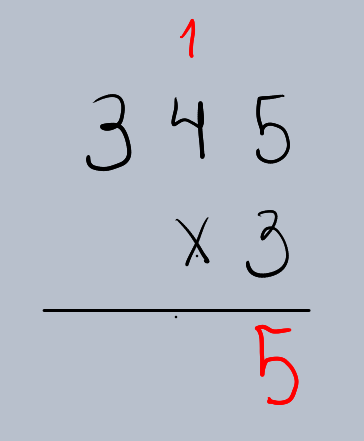
Passo 3: Multiplicar as Dezenas
Multiplique o dígito das dezenas do multiplicando pelo multiplicador e adicione qualquer valor que tenha “subido” da etapa anterior.
•4 (dezenas de 345) x 3 = 12.
•Adicione o 1 que “subiu”: 12 + 1 = 13.
•Escreva o 3 na coluna das dezenas e “suba” o 1 (dezena) para a coluna das centenas
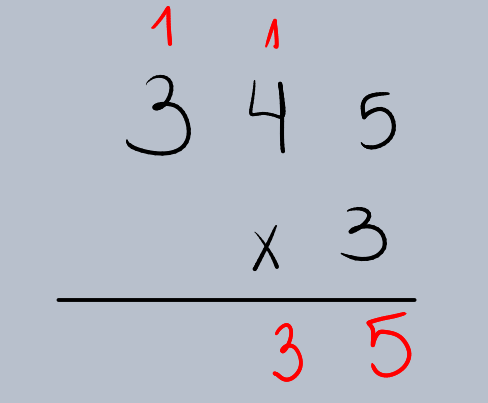
Passo 4: Multiplicar as Centenas
Multiplique o dígito das centenas do multiplicando pelo multiplicador e adicione qualquer valor que tenha “subido” da etapa anterior.
•3 (centenas de 345) x 3 = 9.
•Adicione o 1 que “subiu”: 9 + 1 = 10.
•Escreva o 0 na coluna das centenas e o 1 na coluna dos milhares.
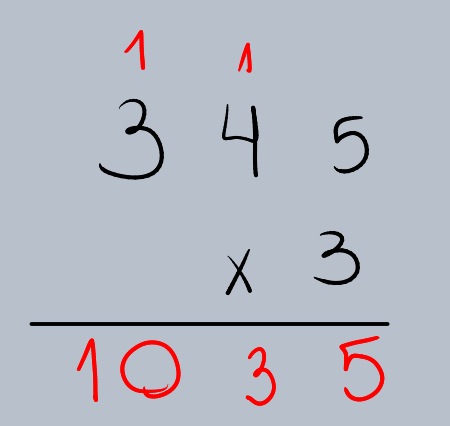
O produto de 345 x 3 é 1035.
Multiplicação por Dois ou Mais Dígitos
Agora, vamos para um exemplo com dois dígitos no multiplicador: 123 x 45.
Passo 1: Armar a Operação
Coloque os números um abaixo do outro, alinhando as unidades.
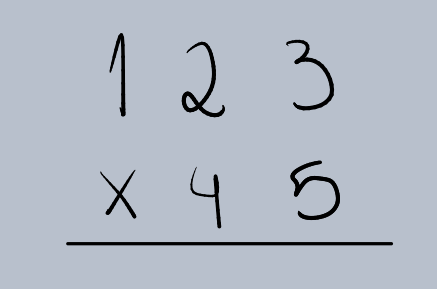
Passo 2: Multiplicar pelo Dígito das Unidades do Multiplicador
Multiplique o multiplicando (123) pelo dígito das unidades do multiplicador (5), seguindo os mesmos passos da multiplicação por um dígito.
•123 x 5 = 615.
•Escreva o resultado abaixo da linha, alinhado com as unidades.
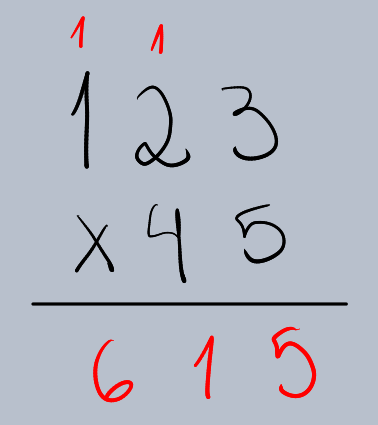
Passo 3: Multiplicar pelo Dígito das Dezenas do Multiplicador
Multiplique o multiplicando (123) pelo dígito das dezenas do multiplicador (4). Lembre-se que o 4 está na casa das dezenas, então seu valor é 40. Por isso, o resultado dessa multiplicação deve começar na coluna das dezenas (ou seja, adicione um zero à direita ou desloque o resultado uma casa para a esquerda).
•123 x 4 = 492.
•Escreva o resultado 492 abaixo do 615, mas deslocado uma casa para a esquerda (ou adicione um zero no final, transformando em 4920).
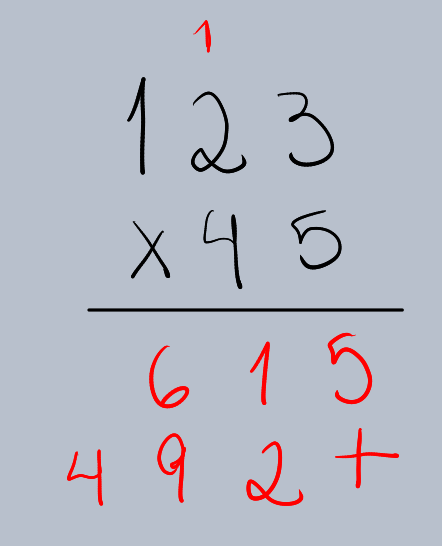
Passo 4: Somar os Produtos Parciais
Agora, some os resultados das multiplicações parciais.
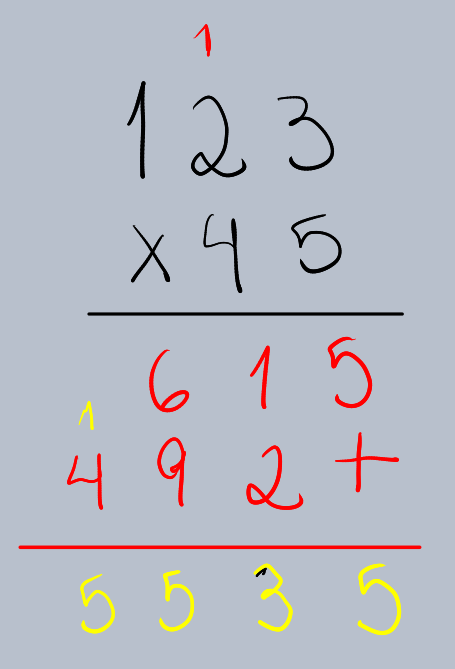
O produto de 123 x 45 é 5535.
Multiplicação com Números Inteiros (Positivos e Negativos)
Até agora, focamos em números naturais (inteiros positivos e zero). No entanto, a multiplicação também se aplica a números inteiros negativos. As regras de sinais são simples, porém fundamentais
1.Positivo vezes positivo sempre dá positivo
•Exemplo: 3 x 4 = 12
2.Negativo vezes negativo sempre dá positivo.
•Exemplo: (-3) x (-4) = 12
•Por que isso acontece? Pense em “tirar uma dívida”. Se você remove (multiplica por um número negativo) três dívidas de 4 reais, seu saldo aumenta em 12 reais (um resultado positivo)
3.O produto de um número positivo por um negativo é sempre negativo, independentemente da ordem
•Exemplo: 3 x (-4) = -12
•Exemplo: (-3) x 4 = -12
•Por que isso acontece? Pense em “adicionar uma dívida”. Se você “adiciona” (multiplica por positivo) 3 dívidas de 4 reais cada, o resultado é que você fica com 12 reais a menos (negativo).
Em resumo, a regra dos sinais é:
•Quando multiplicamos números de sinais iguais, o resultado é sempre positivo.
•Quando multiplicamos números de sinais diferentes, o resultado é sempre negativo
Aplicações Práticas da Multiplicação no Cotidiano
A multiplicação não é apenas um conceito abstrato de sala de aula; ela está presente em diversas situações do nosso dia a dia. Compreender suas aplicações nos ajuda a valorizar sua importância e a utilizá-la de forma eficaz.
•Compras e Finanças:
•Calcular o custo total de vários itens iguais (ex: 5 camisetas a R30cada=5×30=R 30 cada = 5 x 30 = R30cada=5×30=R 150).
•Determinar o valor total de parcelas (ex: 12 parcelas de R250=12×250=R 250 = 12 x 250 = R250=12×250=R 3000).
•Calcular juros simples ou compostos (embora estes envolvam conceitos mais avançados, a multiplicação é a base).
•Culinária e Receitas:
•Mudar a quantidade dos ingredientes para fazer uma receita maior ou menor
•Calcular o tempo total de preparo se cada etapa leva um certo tempo.
•Viagens e Distâncias:
•Estimar a distância total percorrida em uma viagem, sabendo a velocidade média e o tempo (Distância = Velocidade x Tempo).
•Calcular o consumo de combustível (Litros consumidos = Distância / Quilômetros por litro).
•Construção e Design:
•Calcular a área de um cômodo para determinar a quantidade de piso ou tinta necessária.
•Dimensionar materiais (ex: número de tijolos para uma parede).
•Organização e Logística:
•Planejar a capacidade de armazenamento.
•Esportes e Jogos:
•Calcular pontuações em jogos que envolvem múltiplos pontos por ação.
•Determinar o número de combinações possíveis em jogos de tabuleiro ou cartas.
Esses são apenas alguns exemplos de como a multiplicação é uma ferramenta indispensável em nosso cotidiano, facilitando cálculos e auxiliando na tomada de decisões.
Estratégias de Cálculo Mental para Multiplicação
Praticar o cálculo mental é muito útil para resolver problemas mais rápido e entender melhor os números.. Aqui estão algumas estratégias para multiplicar mentalmente:
1. Decomposição de Números
Quebre um dos números em partes menores que sejam mais simples de multiplicar
•Exemplo: 15 x 6
•Pense em 15 como 10 + 5.
•A soma de 60 (produto de 10 por 6) e 30 (produto de 5 por 6) resulta em 90
•Exemplo: 23 x 4
•Pense em 23 como 20 + 3.
•(20 x 4) + (3 x 4) = 80 + 12 = 92.
2. Dobrar e Reduzir pela Metade
Se um dos fatores for par, você pode dobrar um e reduzir o outro pela metade para simplificar a multiplicação.
•Exemplo: 16 x 5
•Mude os números para facilitar: a metade de 16 é 8, e o dobro de 5 é 10
•8 x 10 = 80.
•Exemplo: 14 x 8
•Reduza 14 pela metade (7) e dobre 8 (16).
•No cálculo de 7 x 16, o 16 é desmembrado em (10 + 6). Isso se torna (7 x 10) mais (7 x 6), que é igual a 70 mais 42, resultando em 112
3. Multiplicação por 10, 100, 1000…
Multiplicar por potências de 10 é muito simples: basta adicionar o número de zeros do fator 10, 100, 1000, etc., ao final do outro número.
•Exemplo: 25 x 10 = 250 (adicione um zero)
•Exemplo: 12 x 100 = 1200 (adicione dois zeros)
•Por exemplo, para multiplicar 7 por 1000, basta adicionar os três zeros do 1000 ao 7, resultando em 7000.
4. Aproveitando a proximidade com números como 10, 100, etc., para simplificar o cálculo.
Se um dos fatores estiver próximo de uma potência de 10, você pode usar a propriedade distributiva para facilitar.
•Exemplo: 8 x 9
•Pense em 9 como (10 – 1).
•Oito multiplicado por (10 – 1) é o mesmo que (8 x 10) menos (8 x 1), o que resulta em 80 menos 8, totalizando 72
•Exemplo: 15 x 99
•Pense em 99 como (100 – 1).
•Quinze multiplicado por (100 – 1) é o mesmo que (15 x 100) menos (15 x 1), o que resulta em 1500 menos 15, totalizando 1485
Praticar essas estratégias regularmente pode melhorar significativamente sua agilidade no cálculo mental e sua compreensão da multiplicação.
Relação da Multiplicação com Outras Operações
A matemática é um campo interconectado, e a multiplicação não existe isoladamente. Ela possui relações intrínsecas com a adição, a subtração e, especialmente, com a divisão.
Multiplicação e Adição
Não se esqueça que multiplicar é o mesmo que somar um número várias vezes. Essa é a relação mais direta e fundamental. Entender essa conexão é o primeiro passo para dominar a multiplicação.
Multiplicação e Subtração
A relação com a subtração é mais indireta, mas existe através da propriedade distributiva. Por exemplo, 5 x (7 – 3) pode ser resolvido como (5 x 7) – (5 x 3), o que envolve subtrações.
Multiplicação e Divisão: Operações Inversas
A relação fundamental da multiplicação é com a divisão, sua operação inversa. Se você sabe que 3 x 4 = 12, então você também sabe que 12 dividido por 3 dá 4, e 12 dividido por 4 dá 3.
•Exemplo:
•Se 6 x 7 = 42,
•Então 42 ÷ 6 = 7
•E 42 ÷ 7 = 6
Essa relação é crucial para a resolução de equações e para a compreensão de problemas que envolvem a distribuição ou o agrupamento de quantidades. Se você tem um produto e um dos fatores, a divisão permite encontrar o fator desconhecido.
Conclusão: Multiplicação, Uma Habilidade Essencial
Chegamos ao fim da nossa exploração aprofundada sobre a multiplicação de números inteiros. Esperamos que este artigo tenha desvendado os mistérios dessa operação fundamental, mostrando que ela é muito mais do que apenas memorizar a tabuada. A multiplicação é uma ferramenta universal que possibilita quantificar, comparar e solucionar problemas eficientemente em várias situações.
Vimos novamente que multiplicar é somar várias vezes, olhamos para exemplos com retângulos e combinações, e estudamos suas regras mais importantes: a comutativa, a associativa, a distributiva, e os papéis do número 1 (neutro) e do 0 (nulo). Além disso, detalhamos o algoritmo passo a passo para multiplicar números maiores e compreendemos as regras dos sinais para números inteiros positivos e negativos. As aplicações práticas no cotidiano e as estratégias de cálculo mental reforçam a relevância dessa habilidade.
Dominar a multiplicação é um passo crucial em sua jornada matemática. Ela serve como alicerce para conceitos mais avançados, como frações, decimais, álgebra e cálculo. A prática constante é a chave para a fluência. Não pare de explorar, perguntar e usar o seu conhecimento.. O “Nossa Matemática” está aqui para apoiá-lo em cada etapa do caminho. Continue praticando e desvendando o poder dos números!
Tabuada e a Multiplicação.
A tabuada é, sem dúvida, uma das ferramentas mais importantes no aprendizado da multiplicação. Ela é uma tabela que lista os produtos da multiplicação de um número por outros números inteiros, geralmente de 1 a 10. Dominar a tabuada de cor é fundamental para agilizar os cálculos e construir uma base sólida para conceitos matemáticos mais complexos.
Como a Tabuada Ajuda?
1.Agilidade no Cálculo: Ao invés de realizar a adição repetida ou o algoritmo completo para cada multiplicação simples, a tabuada permite que você acesse o resultado instantaneamente.
2.Base para Cálculos Maiores: A tabuada é a base para a multiplicação de números maiores. Como vimos no algoritmo, multiplicamos dígito por dígito, e esses produtos parciais vêm diretamente da tabuada.
3.Compreensão de Padrões: Ao estudar a tabuada, você começa a perceber padrões e relações entre os números, o que aprofunda sua compreensão numérica.
4.Confiança: Saber a tabuada de cor aumenta a confiança do estudante em suas habilidades matemáticas.
Dicas para Memorizar a Tabuada:
•Comece pelas mais fáceis: As tabuadas do 0, 1, 10 e 5 são geralmente as mais fáceis de memorizar. Comece por elas para construir confiança.
•Tabuada do 0: A regra da tabuada do 0 é fácil: tudo que é multiplicado por zero dá zero
•Tabuada do 1: Todo número vezes 1 dá ele mesmo
•Tabuada do 10: Na tabuada do 10, simplesmente acrescente um zero ao número
•Tabuada do 5: Todos os resultados terão como último algarismo o 0 ou o 5.
•Lembre-se da propriedade comutativa: a ordem dos fatores não altera o resultado, então 3 x 7 é igual a 7 x 3
•Padrões e Truques:
•Tabuada do 9: Os resultados da tabuada do 9 têm uma soma de dígitos igual a 9 (ex: 9×2=18, 1+8=9; 9×3=27, 2+7=9). Além disso, os dígitos das dezenas aumentam e os das unidades diminuem.
•Tabuada do 2: É o dobro do número.
•Tabuada do 4: É o dobro do dobro do número.
•Visualização: Desenhe arranjos retangulares ou grupos de objetos para visualizar os produtos.
multiplicação não é uma invenção recente, mas o resultado de milênios de engenhosidade humana, adaptando-se e evoluindo para atender às crescentes demandas da sociedade.
Para fazer a conta, é só pegar os zeros do 10, 100 ou 1000 e colocá-los no final do outro número.
•Exemplo: 25 x 10 = 250 (adicione um zero)
•Exemplo: 12 x 100 = 1200 (adicione dois zeros)
•Um exemplo simples: 7 vezes 1000 dá 7000. É só pegar o 7 e colocar três zeros no final.
4. Cálculo com números próximos a potências de dez.
Se um dos fatores estiver próximo de uma potência de 10, você pode usar a propriedade distributiva para facilitar.
•Exemplo: 8 x 9
•Pense em 9 como (10 – 1).
•Para facilitar a conta, trocamos o 9 por (10 – 1). Multiplicamos 8 por 10 (dá 80) e tiramos 8 (dá 72)
•Exemplo: 15 x 99
•Pense em 99 como (100 – 1).
•Para calcular 15 vezes 99, podemos pensar no 99 como (100 – 1). Em seguida, distribuímos a multiplicação: 15 vezes 100 é 1500, e 15 vezes 1 é 15. Subtraindo um resultado do outro, 1500 menos 15, chegamos a 1485.
Praticar essas estratégias regularmente pode melhorar significativamente sua agilidade no cálculo mental e sua compreensão da multiplicação.
