Funções Desmistificadas: O Guia Completo para Entender a Relação Entre Números!

Introdução: A Magia das Conexões Matemáticas

Você já parou para pensar como a matemática conecta diferentes ideias e situações? Imagine uma máquina mágica: você insere um número e ela, seguindo uma regra específica, devolve outro número transformado. Essa "máquina" é uma excelente forma de começar a entender o conceito de função, um dos pilares mais importantes da matemática, presente em inúmeras situações do nosso dia a dia, desde calcular o preço de uma compra até prever a trajetória de um foguete!

As funções são como pontes que ligam conjuntos de números, estabelecendo relações claras e previsíveis entre eles. Elas nos ajudam a modelar o mundo ao nosso redor, a entender padrões e a fazer previsões. Seja na física, na biologia, na economia ou na engenharia, as funções estão lá, trabalhando silenciosamente para descrever fenômenos e resolver problemas complexos.

Neste guia completo, vamos desmistificar o conceito de função, explorando suas ideias fundamentais, seus elementos essenciais e seus tipos mais comuns, com foco especial naqueles que você mais encontrará no ensino fundamental e início do médio: a função afim (ou função do 1º grau) e uma introdução à função quadrática (ou função do 2º grau). Nosso objetivo é tornar esse tema, que às vezes parece abstrato, em algo claro, acessível e interessante. Prepare-se para descobrir como as funções organizam o pensamento matemático e como você pode usá-las para entender melhor o universo dos números! Vamos embarcar juntos nesta jornada pelo fascinante mundo das Funções, explorando o Conceito de Função e os principais Tipos de Funções.

1. A Ideia de Função: Relacionando Conjuntos

Para entender o que é uma função, precisamos primeiro revisitar a ideia de conjuntos. Um conjunto é simplesmente uma coleção de objetos ou elementos, que em matemática, frequentemente são números. Imagine dois conjuntos, que chamaremos de Conjunto A e Conjunto B.

Agora, pense em uma forma de relacionar os elementos do Conjunto A com os elementos do Conjunto B. Poderíamos, por exemplo, ligar cada número do Conjunto A ao seu dobro no Conjunto B. Ou talvez ligar cada aluno de uma turma (Conjunto A) à sua idade (Conjunto B).

Uma função é um tipo especial de relação entre dois conjuntos. A definição formal pode parecer um pouco técnica, mas a ideia central é simples: uma função é uma regra que associa cada elemento de um conjunto de partida (chamado Domínio) a um único elemento de um conjunto de chegada (chamado Contradomínio).

O ponto crucial aqui é a palavra "único". Para que uma relação seja considerada uma função, cada elemento do conjunto de partida (Domínio) deve estar associado a exatamente um elemento do conjunto de chegada. Não pode acontecer de um elemento do domínio ficar sem correspondente no contradomínio, nem de um elemento do domínio estar associado a mais de um elemento no contradomínio.

Visualizando com Diagramas de Flechas:

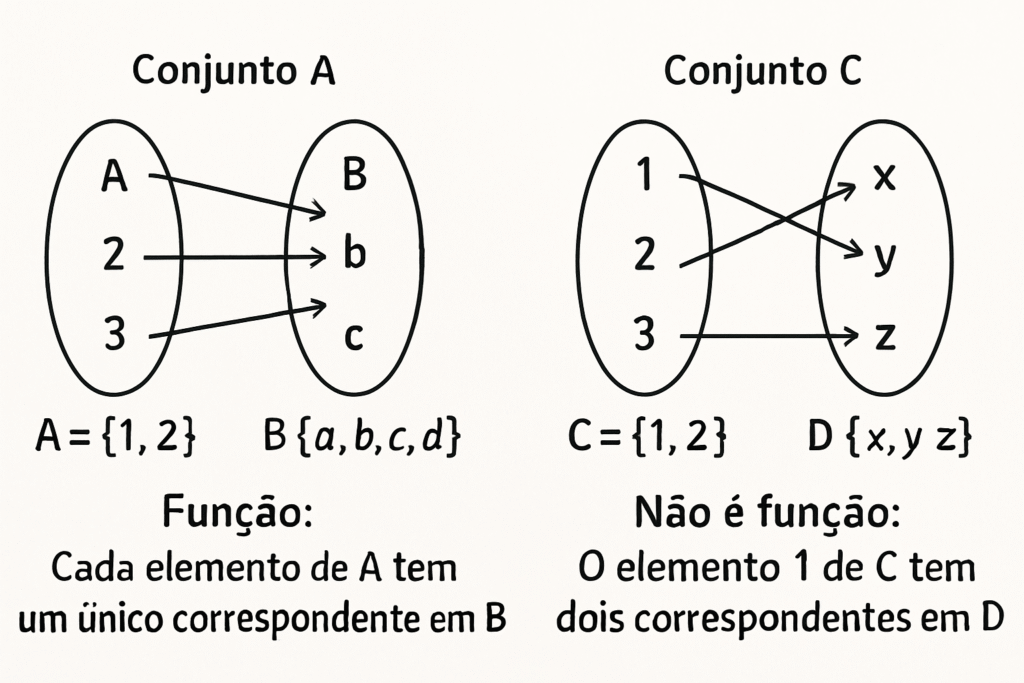
Uma maneira muito útil de visualizar funções (e relações que não são funções) é usando diagramas de flechas. Desenhamos duas ovais (ou retângulos) para representar os conjuntos A e B, colocamos os elementos dentro deles e usamos flechas para indicar as associações.

• É função: Se de cada elemento do Conjunto A (Domínio) parte exatamente uma flecha chegando a algum elemento do Conjunto B (Contradomínio).

• Não é função: Se algum elemento de A não tiver flecha saindo dele, ou se de algum elemento de A sair mais de uma flecha.

Exemplos Simples:

• Dobro de um número: Considere A = {1, 2, 3} e B = {2, 4, 6, 8}. A regra "associar cada número de A ao seu dobro em B" define uma função, pois 1 está associado apenas a 2, 2 apenas a 4, e 3 apenas a 6. Cada elemento de A tem um único correspondente em B.

• Preço em função da quantidade: Se um pão custa R$ 0,50, podemos criar uma função que relaciona a quantidade de pães (Conjunto A: {1, 2, 3, ...}) ao preço total (Conjunto B: {0.50, 1.00, 1.50, ...}). A regra é "multiplicar a quantidade por 0,50". Para cada quantidade, há um único preço total. É uma função.

• Aluno e matérias favoritas: Se A é um conjunto de alunos e B é um conjunto de matérias, a relação "associar cada aluno às suas matérias favoritas" geralmente não é uma função, pois um aluno pode ter mais de uma matéria favorita (mais de uma flecha saindo do mesmo aluno).

Entender essa regra da "associação única" é o primeiro passo fundamental para dominar o conceito de função.

2. Elementos Essenciais de uma Função: Domínio, Contradomínio e Imagem

Toda função possui três componentes fundamentais que precisamos conhecer bem: o Domínio, o Contradomínio e a Imagem. Vamos entender o que cada um representa:

• Domínio (D ou Dom(f)): É o conjunto de partida da função. Ele contém todos os valores de entrada possíveis para a função, ou seja, todos os valores que a variável independente (geralmente representada por x) pode assumir. No diagrama de flechas, é o primeiro conjunto (de onde partem as flechas).

• Contradomínio (CD ou CD(f)): É o conjunto de chegada da função. Ele contém todos os valores que poderiam ser resultado da aplicação da função, ou seja, todos os possíveis valores de saída. No diagrama de flechas, é o segundo conjunto (onde chegam as flechas).

• Imagem (Im ou Im(f)): É um subconjunto do Contradomínio. A Imagem é formada apenas pelos valores que realmente são resultado da aplicação da função a algum elemento do Domínio. Em outras palavras, são os valores da variável dependente (geralmente representada por y ou f(x)) que possuem um correspondente no Domínio. No diagrama de flechas, são os elementos do Contradomínio que efetivamente recebem alguma flecha.

Notação Importante:

Costumamos representar uma função f que leva elementos do conjunto A para o conjunto B da seguinte forma: f: A → B. Isso lê-se "função f de A em B", onde A é o Domínio e B é o Contradomínio.

A regra que define a função é frequentemente escrita como y = f(x). Isso lê-se "y é igual a f de x", indicando que o valor de y (a saída, pertencente à Imagem) depende do valor de x (a entrada, pertencente ao Domínio) através da regra definida por f.

Identificando os Elementos:

Vamos voltar ao exemplo da função "dobro de um número" com A = {1, 2, 3} e B = {2, 4, 6, 8}.

• Domínio (D): É o conjunto A inteiro: D = {1, 2, 3}.

• Contradomínio (CD): É o conjunto B inteiro: CD = {2, 4, 6, 8}.

• Imagem (Im): São os valores em B que realmente foram usados como resultado: Im = {2, 4, 6}. Note que o número 8 pertence ao Contradomínio, mas não à Imagem, pois nenhum elemento do Domínio, quando dobrado, resulta em 8.

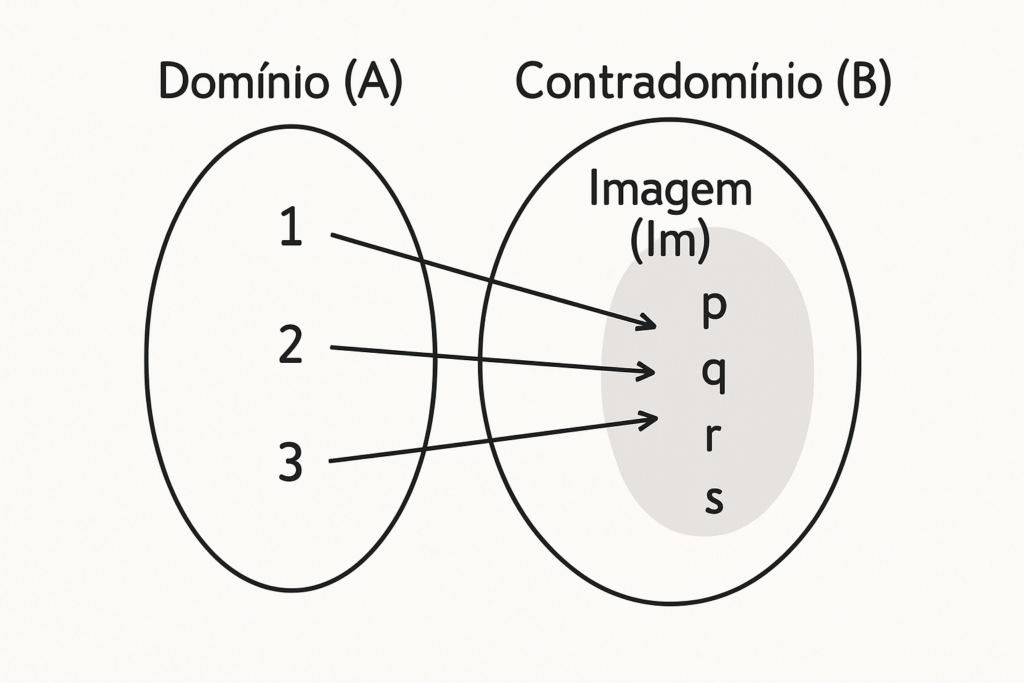
Compreender a diferença entre Contradomínio (o que poderia ser) e Imagem (o que realmente é) é essencial. A Imagem está sempre contida dentro do Contradomínio (Im ⊆ CD).

3. Representando Funções: Fórmulas, Tabelas e Gráficos

Existem diferentes maneiras de representar uma função, cada uma com suas vantagens para entender e trabalhar com a relação entre as variáveis. As formas mais comuns são a lei de formação (fórmula), as tabelas e os gráficos.

• Lei de Formação (Fórmula): Esta é talvez a forma mais comum de encontrar funções em matemática. A lei de formação é a regra matemática explícita que descreve como obter o valor de saída (y ou f(x)) a partir do valor de entrada (x). Por exemplo:

  • f(x) = 2x + 1 (Função Afim)

  • g(x) = x² - 3 (Função Quadrática)

  • h(x) = 5 (Função Constante) A fórmula nos permite calcular o valor da função para qualquer x pertencente ao domínio.

• Tabelas: As tabelas são úteis para organizar e visualizar alguns pares de valores (entrada, saída) da função. Construímos uma tabela com duas colunas (ou linhas): uma para os valores de x (do domínio) e outra para os valores correspondentes de y = f(x) (da imagem).

  Exemplo para f(x) = 2x + 1:

  x

  y = f(x) = 2x + 1

  -1

  2(-1) + 1 = -1

  0

  2(0) + 1 = 1

  1

  2(1) + 1 = 3

  2

  2(2) + 1 = 5

  As tabelas nos dão uma visão pontual do comportamento da função.

• Gráficos: A representação gráfica é uma das ferramentas mais poderosas para entender funções, pois nos dá uma visualização completa do seu comportamento no plano cartesiano.

  • O plano cartesiano é formado por dois eixos perpendiculares: o eixo horizontal (eixo x ou eixo das abscissas), onde representamos os valores do domínio, e o eixo vertical (eixo y ou eixo das ordenadas), onde representamos os valores do contradomínio/imagem.

  • Cada par ordenado (x, y) ou (x, f(x)) da função corresponde a um ponto no plano cartesiano.

  • O gráfico de uma função é o conjunto de todos os pontos (x, f(x)) que satisfazem a lei de formação da função, para todos os x no domínio. Ele forma uma linha, uma curva ou um conjunto de pontos que representa visualmente a relação.

  Teste da Linha Vertical: Uma característica importante do gráfico de qualquer função é que nenhuma linha vertical pode interceptá-lo em mais de um ponto. Isso ocorre porque, para cada x do domínio, existe apenas um único y correspondente. Se uma linha vertical cortar o gráfico em dois ou more pontos, significa que para aquele valor de x, existem múltiplos valores de y, e portanto, a relação representada não é uma função.

Dominar essas três formas de representação – fórmula, tabela e gráfico – e saber transitar entre elas é fundamental para trabalhar com funções de maneira eficaz.

4. Tipos Comuns de Funções: Constante, Afim e Quadrática

Embora existam muitos tipos de funções na matemática, no ensino fundamental e início do médio, focamos principalmente em algumas famílias básicas. Vamos conhecer as mais importantes:

• Função Constante: É o tipo mais simples de função. Sua lei de formação é f(x) = k, onde 'k' é um número real constante. Isso significa que, não importa qual valor de x você escolha no domínio, o resultado será sempre o mesmo valor k.

  • Exemplo: f(x) = 3. Para x=1, f(1)=3. Para x=-5, f(-5)=3. Para x=100, f(100)=3.

  • Gráfico: O gráfico de uma função constante é sempre uma linha reta horizontal na altura y = k.

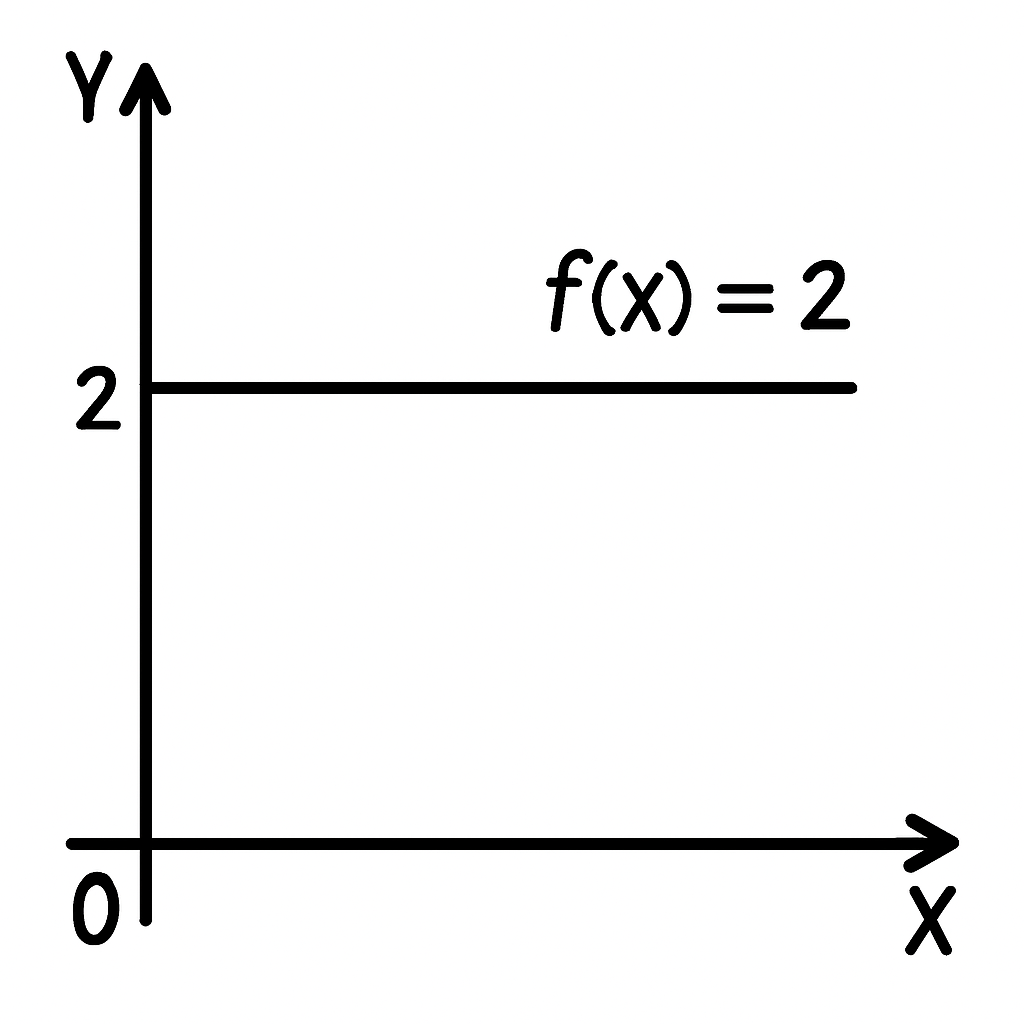
• Função Afim (ou Função do 1º Grau): Esta é uma das funções mais estudadas e aplicadas. Sua lei de formação é f(x) = ax + b, onde 'a' e 'b' são números reais e, crucialmente, a ≠ 0 (se a=0, ela se torna uma função constante).

  • Coeficientes:

    • a: Chamado de coeficiente angular ou taxa de variação. Ele determina a inclinação da reta que representa a função. Se a > 0, a função é crescente (a reta sobe da esquerda para a direita). Se a < 0, a função é decrescente (a reta desce da esquerda para a direita).

    • b: Chamado de coeficiente linear ou intercepto y. Ele indica o ponto onde o gráfico da função corta o eixo y. Esse ponto tem coordenadas (0, b).

  • Gráfico: O gráfico de uma função afim é sempre uma linha reta.

  • Raiz ou Zero da Função: É o valor de x para o qual f(x) = 0. Geometricamente, é o ponto onde a reta corta o eixo x. Para encontrar a raiz, resolvemos a equação ax + b = 0, que nos dá x = -b/a.

• Função Linear: É um caso particular da função afim onde o coeficiente linear b = 0. Sua lei de formação é f(x) = ax (com a ≠ 0).

  • Exemplo: f(x) = 3x, g(x) = -0.5x.

  • Gráfico: O gráfico de uma função linear é sempre uma reta que passa pela origem do plano cartesiano, o ponto (0, 0).

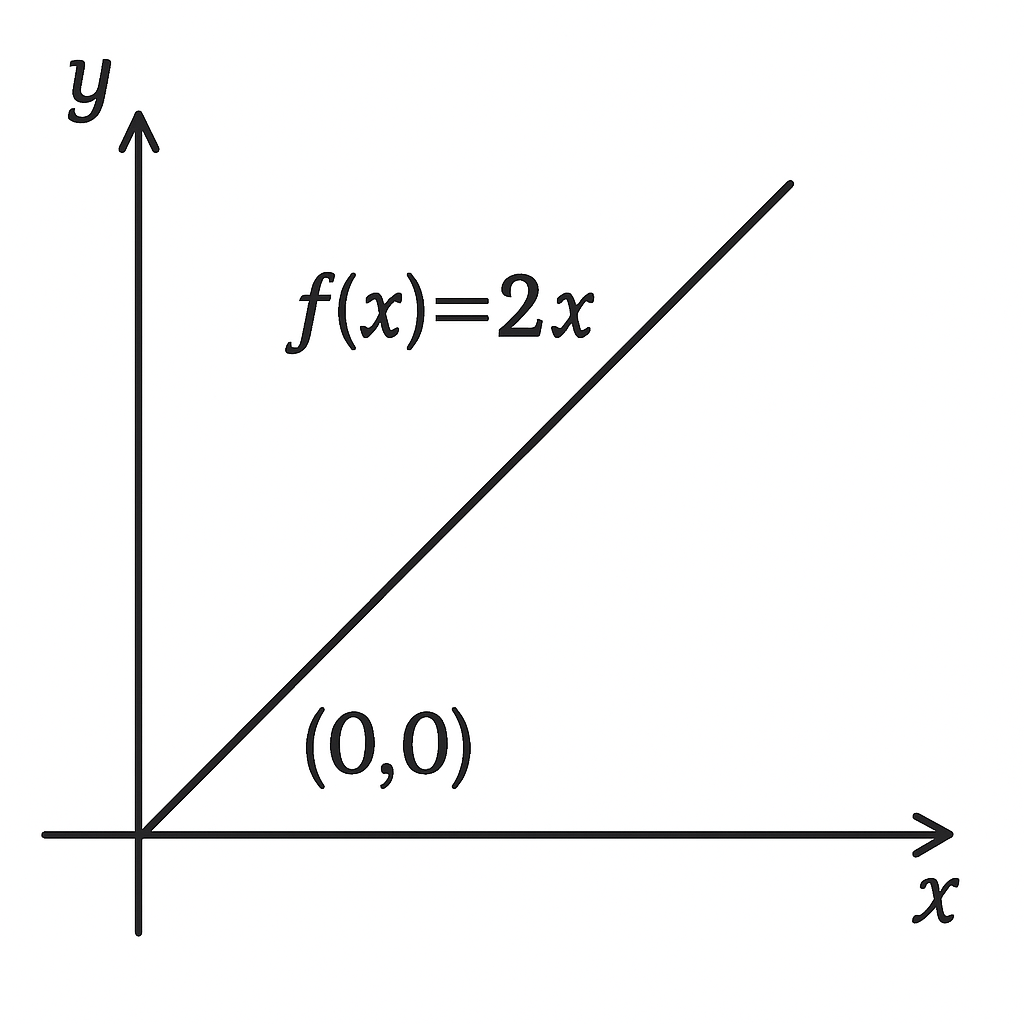
• Função Quadrática (ou Função do 2º Grau): Damos aqui uma introdução a este tipo de função, que você estudará mais a fundo posteriormente. Sua lei de formação é f(x) = ax² + bx + c, onde a, b e c são números reais e, fundamentalmente, a ≠ 0 (se a=0, ela se torna uma função afim).

  • Gráfico: O gráfico de uma função quadrática é uma curva chamada parábola.

  • Concavidade: A direção para onde a parábola se abre (sua "boca") é determinada pelo sinal do coeficiente 'a'. Se a > 0, a parábola tem concavidade voltada para cima (😊). Se a < 0, a parábola tem concavidade voltada para baixo (😟).

  • Vértice: É o ponto mais baixo (se a>0) ou mais alto (se a<0) da parábola. Ele representa o ponto de mínimo ou máximo valor da função.

  • Raízes ou Zeros da Função: São os valores de x para os quais f(x) = 0. Geometricamente, são os pontos onde a parábola corta ou toca o eixo x. Encontrar as raízes de uma função quadrática é o mesmo que resolver a equação do segundo grau ax² + bx + c = 0, geralmente usando a fórmula de Bhaskara. O número de raízes reais (duas, uma ou nenhuma) depende do valor do discriminante (Δ = b² - 4ac).

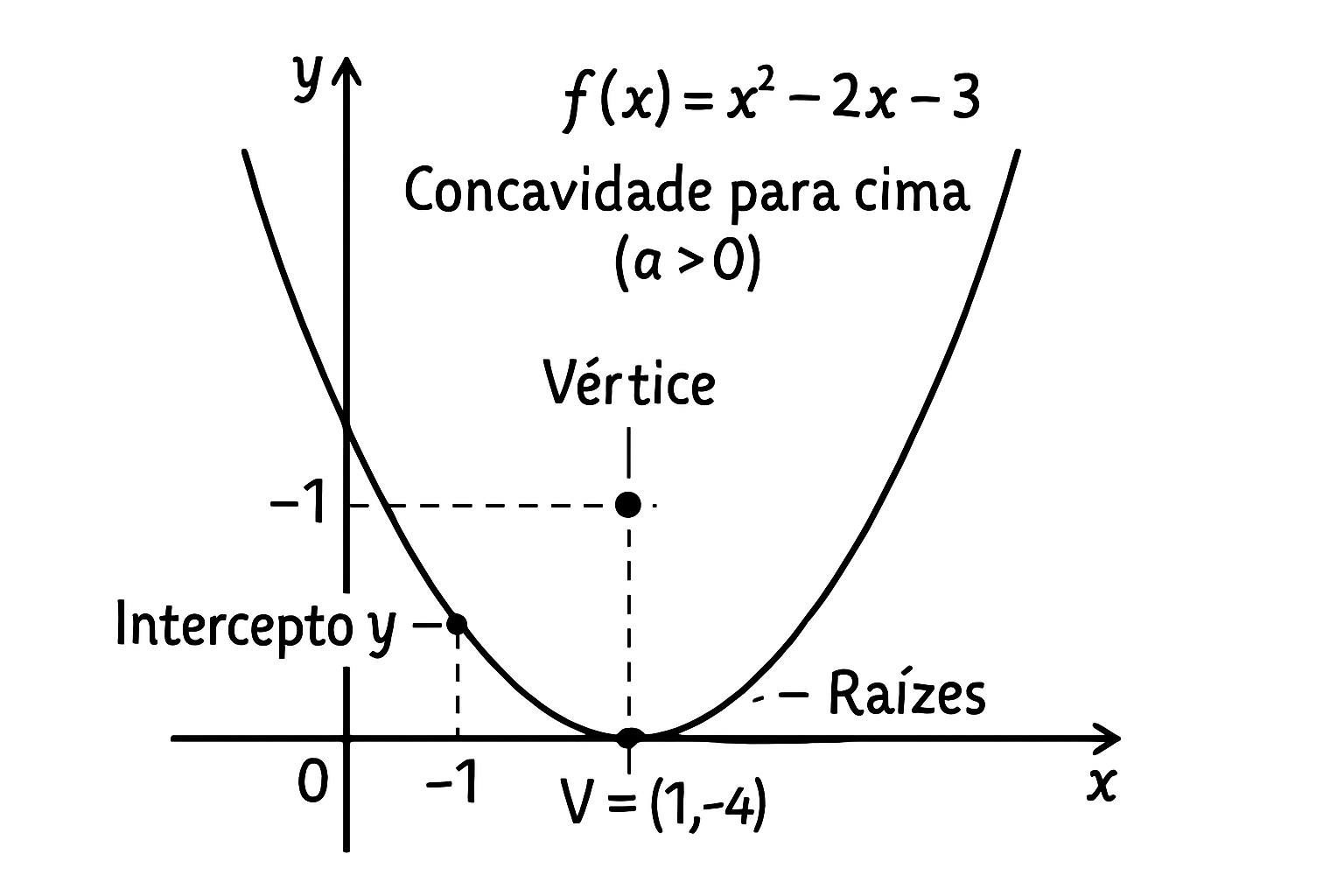
Compreender as características e os gráficos desses tipos básicos de funções é essencial para construir uma base sólida em matemática.

5. Analisando Gráficos de Funções: Lendo a Imagem Matemática

O gráfico de uma função é uma fonte riquíssima de informações. Aprender a "ler" um gráfico significa ser capaz de extrair dele diversas características importantes da função sem precisar da sua fórmula. Vamos ver o que podemos analisar:

• Domínio e Imagem:

  • Domínio: Projetando todos os pontos do gráfico sobre o eixo x, o conjunto de valores cobertos no eixo x representa o domínio da função.

  • Imagem: Projetando todos os pontos do gráfico sobre o eixo y, o conjunto de valores cobertos no eixo y representa a imagem da função.

• Crescimento e Decrescimento:

  • Função Crescente: Em um intervalo do domínio, a função é crescente se, ao percorrermos o gráfico da esquerda para a direita, a linha ou curva está subindo.

  • Função Decrescente: Em um intervalo do domínio, a função é decrescente se, ao percorrermos o gráfico da esquerda para a direita, a linha ou curva está descendo.

  • Função Constante: Em um intervalo do domínio, a função é constante se o gráfico é uma linha horizontal.

• Raízes (Interceptos x): São os pontos onde o gráfico corta ou toca o eixo x. Nesses pontos, o valor de y (ou f(x)) é sempre zero.

• Intercepto y: É o ponto onde o gráfico corta o eixo y. Nesse ponto, o valor de x é sempre zero. O valor de y nesse ponto é f(0).

• Valores Específicos: Podemos encontrar o valor da função para um x específico (f(a)) localizando 'a' no eixo x, subindo (ou descendo) verticalmente até encontrar o gráfico e, então, movendo-se horizontalmente até o eixo y para ler o valor correspondente. Da mesma forma, podemos encontrar o(s) valor(es) de x para um y específico (f(x)=b) localizando 'b' no eixo y, movendo-se horizontalmente até encontrar o gráfico e, então, descendo (ou subindo) verticalmente até o eixo x.

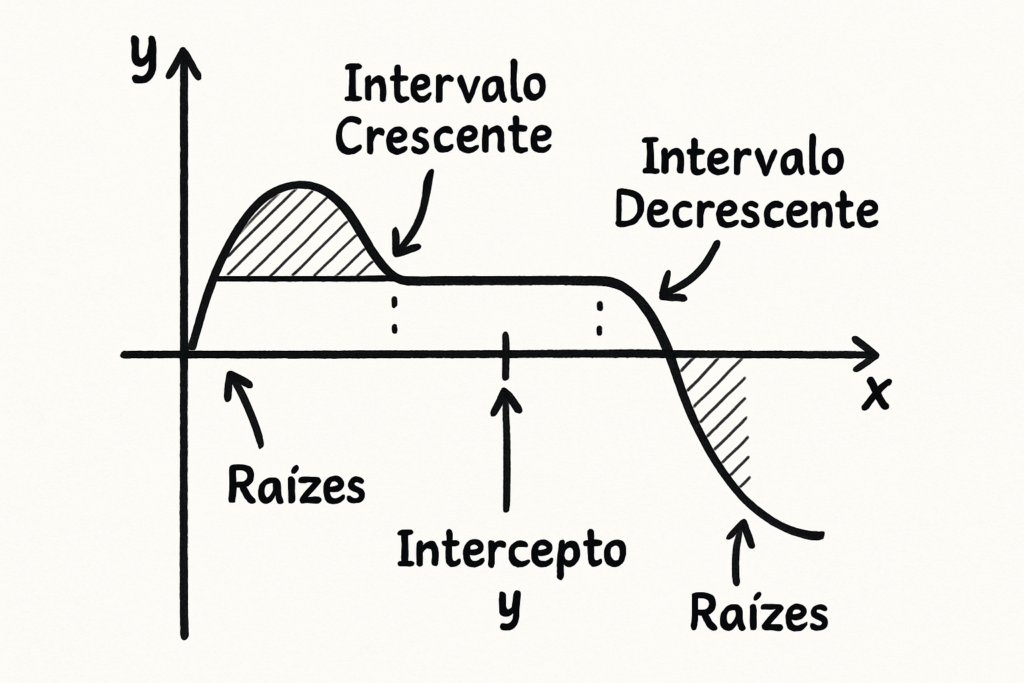
A habilidade de interpretar gráficos é crucial não apenas em matemática, mas em diversas áreas que utilizam representações visuais de dados.

6. Aplicações Práticas das Funções: A Matemática no Mundo Real

As funções não são apenas conceitos abstratos; elas são ferramentas poderosas para modelar e entender situações do nosso cotidiano e fenômenos naturais. Vejamos alguns exemplos:

• Economia e Finanças:

  • Custo Total: O custo para produzir 'x' unidades de um produto pode ser modelado por uma função. Muitas vezes, há um custo fixo (b) e um custo por unidade (a), resultando em uma função afim: C(x) = ax + b.

  • Preço da Compra: O valor total a pagar por 'x' quilogramas de um produto que custa 'a' reais por quilo é uma função linear: P(x) = ax.

  • Juros Simples: O montante após um certo tempo pode ser descrito por uma função afim do tempo.

• Física:

  • Movimento Uniforme: A distância percorrida por um objeto em velocidade constante 'v' em função do tempo 't' é uma função linear: d(t) = vt.

  • Movimento Uniformemente Variado: A posição de um objeto em aceleração constante envolve uma função quadrática do tempo.

  • Lançamento de Projéteis: A altura de um objeto lançado verticalmente para cima (desconsiderando a resistência do ar) em função do tempo é descrita por uma função quadrática, formando uma parábola.

• Biologia:

  • Crescimento Populacional: Modelos simples de crescimento de populações (bactérias, por exemplo) podem usar funções (muitas vezes exponenciais, um tipo que veremos mais adiante).

  • Metabolismo: A relação entre a dose de um medicamento e seu efeito no corpo pode ser modelada por funções.

• Situações Cotidianas:

  • Conta de Energia/Água: O valor da conta frequentemente depende do consumo através de uma função definida por faixas de consumo.

  • Temperatura: A variação da temperatura ao longo de um dia pode ser representada graficamente por uma função do tempo.

  • Receitas Culinárias: A quantidade de ingredientes necessária pode ser vista como uma função do número de porções desejadas.

Perceber como as funções descrevem essas relações nos ajuda a entender melhor o mundo e a tomar decisões mais informadas.

7. Resumo e Dicas Finais: Organizando as Ideias

Chegamos ao final da nossa exploração inicial sobre funções. Vamos recapitular os pontos mais importantes e algumas dicas para você continuar seus estudos:

Conceitos Chave:

• Função: Uma regra que associa cada elemento do Domínio a um único elemento do Contradomínio.

• Domínio (D): Conjunto de entrada (valores de x).

• Contradomínio (CD): Conjunto de chegada (possíveis valores de y).

• Imagem (Im): Conjunto dos valores de y que são efetivamente resultado da função (Im ⊆ CD).

• Representações: Lei de Formação (fórmula), Tabelas e Gráficos (plano cartesiano).

• Teste da Linha Vertical: Ajuda a identificar se um gráfico representa uma função.

Principais Tipos Abordados:

• Função Constante (f(x) = k): Gráfico é uma reta horizontal.

• Função Afim (f(x) = ax + b, a≠0): Gráfico é uma reta inclinada. 'a' é o coeficiente angular (inclinação), 'b' é o coeficiente linear (intercepto y). Raiz: x = -b/a.

• Função Linear (f(x) = ax, a≠0): Caso particular da afim (b=0). Gráfico é uma reta inclinada passando pela origem.

• Função Quadrática (f(x) = ax² + bx + c, a≠0): Gráfico é uma parábola. Concavidade depende de 'a'. Possui vértice e pode ter 0, 1 ou 2 raízes reais.

Dicas para Resolver Problemas:

1. Leia com Atenção: Entenda o que o problema pede e quais informações são fornecidas.

2. Identifique a Função: Determine o tipo de função envolvida (constante, afim, quadrática?) ou sua lei de formação, se fornecida.

3. Use a Representação Adequada: Às vezes, a fórmula é mais útil; outras vezes, construir uma tabela ou esboçar o gráfico pode clarear as ideias.

4. Interprete os Coeficientes: Em funções afins e quadráticas, entenda o significado de 'a', 'b' e 'c'.

5. Traduza a Pergunta: Converta a pergunta do problema em termos matemáticos (encontrar f(x) para um dado x, encontrar x para um dado f(x), encontrar a raiz, o vértice, etc.).

6. Verifique a Resposta: Faz sentido o resultado encontrado no contexto do problema?

8. Conclusão: As Funções Como Ferramenta Essencial

Exploramos o conceito fundamental de função, seus elementos, representações e alguns tipos importantes como a função afim e a quadrática. Vimos como as funções são essenciais não apenas na matemática pura, mas também como ferramentas poderosas para descrever e analisar o mundo ao nosso redor.

Dominar o conceito de função abre portas para muitos outros tópicos fascinantes da matemática e de outras ciências. Continue praticando, explorando exemplos e, principalmente, tentando conectar essas ideias com situações reais. A matemática se torna muito mais interessante quando percebemos sua aplicação e sua capacidade de organizar nosso pensamento!

Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=Wby7lf-Llek

Canal: Descomplica

http://www.youtube.com/watch?v=ZafklDSTDUg

Canal: Professor Possani