Desvende a Matemática: Evite os Erros Mais Comuns e Turbine Seus Estudos

Introdução: A Matemática no Centro do Desafio e da Solução

A matemática. Para alguns, uma linguagem universal fascinante, a chave para desvendar os segredos do universo e a base para inúmeras carreiras de sucesso. Para outros, um campo minado de regras complexas, símbolos abstratos e uma fonte constante de frustração. Independentemente de como você a percebe, a verdade é inegável: a matemática permeia nosso cotidiano e é uma ferramenta fundamental no mundo acadêmico e profissional. Seja você um estudante do ensino médio preparando-se para o ENEM e vestibulares, um universitário navegando por cálculos e disciplinas exatas, ou um concurseiro buscando a aprovação em provas que exigem raciocínio lógico e quantitativo, dominar a matemática é, muitas vezes, um diferencial crucial.

Contudo, a jornada para essa maestria frequentemente é marcada por tropeços. Quem nunca se sentiu perdido em meio a uma equação, cometeu um erro de sinal que comprometeu todo o resultado ou sentiu que, por mais que estudasse, certos conceitos simplesmente não "entravam" na cabeça? Essa dificuldade em matemática é mais comum do que se imagina e, muitas vezes, a raiz do problema não está em uma suposta falta de aptidão, mas sim na repetição de erros comuns que poderiam ser evitados.

A boa notícia é que esses obstáculos não são intransponíveis. A frustração pode dar lugar à confiança quando entendemos onde estamos errando e, principalmente, como estudar matemática de forma mais eficaz. Este post é o seu guia nessa jornada. Vamos mergulhar fundo nos erros mais frequentes cometidos por estudantes como você – desde falhas técnicas em cálculos básicos até armadilhas nas estratégias de estudo – e apresentar caminhos claros e práticos para evitá-los. Nosso objetivo é fornecer as ferramentas e insights necessários para que você não apenas corrija seus erros, mas transforme sua relação com a matemática, tornando seu aprendizado mais sólido, eficiente e, quem sabe, até prazeroso. Prepare-se para desvendar os segredos por trás dos erros e turbinar seus estudos!

Parte 1: Desvendando os Erros Técnicos Mais Frequentes

Mesmo com a melhor das intenções e horas dedicadas ao estudo, alguns erros técnicos podem minar seu progresso em matemática. São aqueles deslizes em conceitos fundamentais ou na aplicação de regras que, embora pareçam pequenos, podem levar a resultados completamente equivocados e gerar uma enorme frustração. Identificar e corrigir esses erros comuns em matemática básica é o primeiro passo para construir uma base sólida e avançar com mais segurança. Vamos analisar os tropeços conceituais e de cálculo mais frequentes que assombram estudantes do ensino médio, universitários e concurseiros.

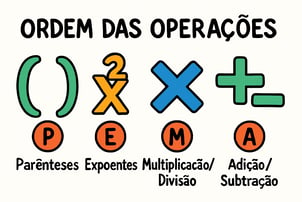
Erro 1: A Ordem das Operações – A Hierarquia Ignorada (PEMDAS/BODMAS)

Talvez o erro mais fundamental e, ainda assim, incrivelmente comum, seja ignorar a ordem correta das operações matemáticas. Em expressões que envolvem diferentes operações (adição, subtração, multiplicação, divisão, potenciação, radiciação) e agrupamentos (parênteses, colchetes, chaves), existe uma hierarquia clara que deve ser seguida para garantir o resultado correto. No Brasil, é comum usar a sigla PEMDAS (Parênteses, Expoentes, Multiplicação e Divisão – da esquerda para a direita, Divisão e Multiplicação têm a mesma prioridade, Adição e Subtração – da esquerda para a direita, Adição e Subtração têm a mesma prioridade) como guia.

A Falha Clássica: Considere a expressão 3 + 5 * 2. Um erro comum é realizar a adição primeiro: 3 + 5 = 8, e depois multiplicar por 2, chegando a 16. No entanto, a multiplicação tem prioridade sobre a adição.

O Cálculo Correto: Seguindo a ordem PEMDAS, primeiro realizamos a multiplicação: 5 * 2 = 10. Depois, a adição: 3 + 10 = 13. O resultado correto é 13, bem diferente de 16.

Como Evitar:

•Memorize a Ordem: Use mnemônicos como PEMDAS ou lembre-se da sequência: 1º Parênteses/Colchetes/Chaves (do mais interno para o mais externo), 2º Expoentes e Raízes, 3º Multiplicação e Divisão (na ordem em que aparecem, da esquerda para a direita), 4º Adição e Subtração (na ordem em que aparecem, da esquerda para a direita).

•Use Parênteses: Na dúvida, ou para tornar a expressão mais clara, use parênteses para indicar explicitamente a ordem que você deseja seguir. Por exemplo, se a intenção fosse somar primeiro (o que geralmente não é o caso sem parênteses explícitos), você escreveria (3 + 5) * 2.

•Pratique: Resolva expressões variadas, aumentando gradualmente a complexidade, para internalizar a regra.

Erro 2: Confusão com Sinais (+/-) – O Jogo Perigoso do Positivo e Negativo

Ah, os sinais! Uma pequena troca entre + e - pode causar um estrago considerável. Esse erro é frequente tanto em operações aritméticas básicas quanto na manipulação de expressões algébricas e equações. A atenção aos detalhes é crucial aqui.

A Falha Clássica: Ao resolver a equação 2x - 7 = 3, um erro comum é mover o -7 para o outro lado e esquecer de trocar o sinal, resultando em 2x = 3 - 7, que leva a 2x = -4 e x = -2. Outro erro comum é na multiplicação ou divisão: calcular -5 * -3 como -15.

O Cálculo Correto: Ao mover um termo que está subtraindo para o outro lado da igualdade, ele passa somando: 2x = 3 + 7, que leva a 2x = 10 e x = 5. Na multiplicação de sinais iguais, o resultado é positivo: -5 * -3 = +15.

Como Evitar:

•Regra de Sinais: Tenha a regra de sinais sempre em mente: (+) (+) = +, (-) (-) = +, (+) (-) = -, (-) (+) = -. O mesmo vale para a divisão.

•Passo a Passo: Ao manipular equações, faça um passo de cada vez. Ao mover um termo, reescreva a equação inteira com o sinal corrigido antes de prosseguir.

•Verificação: Após encontrar a solução de uma equação, substitua o valor encontrado na equação original para verificar se a igualdade se mantém. Se x = 5 na equação 2x - 7 = 3, temos 2*(5) - 7 = 10 - 7 = 3, o que confirma a solução.

Erro 3: Unidades de Medida – As Grandes Esquecidas (e Perigosas)

Em problemas que envolvem grandezas físicas, químicas ou situações práticas do dia a dia, esquecer ou misturar unidades de medida é um erro fatal. A resposta pode estar numericamente correta, mas se a unidade estiver errada ou ausente, o resultado perde todo o sentido. Isso é especialmente crítico em matemática para concursos e na matemática universitária, onde a aplicação em contextos reais é frequente.

A Falha Clássica: Calcular a área de um terreno retangular com lados medindo 50 metros e 0,2 quilômetros. Multiplicar diretamente 50 * 0,2 = 10 e apresentar a resposta como 10 m² ou 10 km² está incorreto.

O Cálculo Correto: Primeiro, converta as unidades para que sejam consistentes. Podemos converter 0,2 km para metros: 0,2 km 1000 m/km = 200 m. Agora, calculamos a área: 50 m 200 m = 10.000 m². Ou, convertemos 50 m para quilômetros: 50 m / 1000 m/km = 0,05 km. A área seria 0,05 km * 0,2 km = 0,01 km². Ambas as respostas (10.000 m² e 0,01 km²) estão corretas e são equivalentes, mas a unidade deve ser explicitada.

Como Evitar:

•Anote Sempre: Ao extrair dados de um problema, anote os valores junto com suas respectivas unidades.

•Padronize: Antes de iniciar qualquer cálculo, converta todas as grandezas para um mesmo sistema de unidades (geralmente o Sistema Internacional - SI, ou o sistema pedido no problema).

•Análise Dimensional: Use as unidades como guia durante os cálculos. Se você está calculando uma área (m * m), sua resposta final deve ter unidade de m². Se as unidades não "fecharem", você provavelmente cometeu um erro na fórmula ou na conversão.

Erro 4: Percentual – Simples na Aparência, Complicado na Prática?

Cálculos de porcentagem são onipresentes – descontos, juros, estatísticas, notas. Apesar de parecerem simples, geram muitos erros, especialmente em aumentos e descontos sucessivos ou no cálculo de variação percentual.

A Falha Clássica: Calcular um aumento de 10% seguido de um desconto de 10% sobre um valor de R$ 100,00 e concluir que o valor final volta a ser R$ 100,00. Outro erro é calcular 20% de 50 como 20 * 50.

O Cálculo Correto: Aumento de 10% sobre R$ 100,00: 100 (1 + 0,10) = R$ 110,00. Desconto de 10% sobre o novo valor (R$ 110,00): 110 (1 - 0,10) = 110 0,90 = R$ 99,00. O valor final não é R$ 100,00! Para calcular 20% de 50, transformamos a porcentagem em decimal ou fração: 0,20 50 = 10 ou (20/100) * 50 = 10.

Como Evitar:

•Entenda o Conceito: Porcentagem significa "por cem". 20% é o mesmo que 20/100 ou 0,20.

•Base de Cálculo: Preste atenção sobre qual valor a porcentagem está sendo calculada, especialmente em aumentos/descontos sucessivos (a base muda a cada passo).

•Fator de Multiplicação: Use fatores de multiplicação para agilizar: Aumentar X% é multiplicar por (1 + X/100). Descontar X% é multiplicar por (1 - X/100).

•Pratique: Resolva problemas variados envolvendo porcentagens em diferentes contextos (juros simples e compostos, lucro, prejuízo, etc.).

Erro 5: Potências e Expoentes – As Regras que Embaraçam

Potenciação é uma operação fundamental, mas suas regras podem ser confusas. Erros comuns incluem somar expoentes de potências com bases diferentes, tratar o expoente zero ou negativo de forma incorreta, ou confundir (-a)^n com -a^n.

A Falha Clássica: Calcular 2³ 5² como (25)^(3+2) = 10⁵. Outro erro: achar que 3⁰ = 0 ou que 2⁻³ = -8.

O Cálculo Correto: Só podemos somar os expoentes na multiplicação de potências de mesma base (a^m a^n = a^(m+n)). Quando as bases são diferentes, calculamos cada potência separadamente: 2³ 5² = 8 * 25 = 200. Qualquer número (exceto zero) elevado a zero é igual a 1: 3⁰ = 1. Um expoente negativo inverte a base: 2⁻³ = (1/2)³ = 1/8. Atenção aos parênteses: (-2)⁴ = 16, enquanto -2⁴ = -(2⁴) = -16.

Como Evitar:

•Revise as Propriedades: Dedique tempo para entender e memorizar as propriedades da potenciação (produto de mesma base, quociente de mesma base, potência de potência, etc.).

•Pratique com Números: Antes de aplicar em álgebra, pratique as regras com exemplos numéricos simples para ganhar confiança.

•Atenção aos Parênteses: Os parênteses indicam o que está sendo elevado à potência. Sua presença ou ausência muda completamente o resultado quando a base é negativa.

Erro 6: Regra de Três – Quando a Simplicidade Engana

A regra de três é uma ferramenta poderosa para resolver problemas de proporcionalidade, muito usada por concurseiros e no ensino médio. O erro surge ao aplicar a regra de três simples (envolvendo apenas duas grandezas) em problemas que envolvem três ou mais grandezas (regra de três composta) ou ao não identificar corretamente se a relação entre as grandezas é direta ou inversamente proporcional.

A Falha Clássica: Problema: "Se 4 impressoras imprimem 1000 páginas em 2 horas, quantas horas levarão 8 impressoras para imprimir 3000 páginas?". Tentar resolver isso com uma única regra de três simples, ignorando uma das grandezas ou a relação entre elas.

O Cálculo Correto (Usando Regra de Três Composta): Organize as grandezas e a incógnita (horas = x): Impressoras | Páginas | Horas 4 | 1000 | 2 8 | 3000 | x

Analise a proporcionalidade de cada grandeza com a grandeza da incógnita (Horas):

•Impressoras e Horas: Quanto MAIS impressoras, MENOS horas (Inversamente Proporcional - I.P.).

•Páginas e Horas: Quanto MAIS páginas, MAIS horas (Diretamente Proporcional - D.P.).

Monte a proporção, invertendo a razão da grandeza I.P.: 2/x = (8/4) (1000/3000) (Invertemos 4/8 para 8/4 por ser I.P.) 2/x = 2 (1/3) 2/x = 2/3 2x = 6 x = 3 horas.

Como Evitar:

•Identifique as Grandezas: Liste todas as grandezas envolvidas no problema.

•Analise a Proporcionalidade: Compare cada grandeza com a grandeza da incógnita, uma de cada vez, mantendo as outras constantes. Pergunte: "Se eu aumentar esta grandeza, a incógnita aumenta ou diminui?".

•Monte a Proporção: Coloque a razão da incógnita de um lado da igualdade. Do outro lado, multiplique as razões das outras grandezas. Importante: Inverta as razões das grandezas que forem inversamente proporcionais à incógnita.

•Resolva: Isole a incógnita e calcule o resultado.

Dominar esses aspectos técnicos é como afiar suas ferramentas antes de construir algo grandioso. Ao evitar esses erros de cálculo e conceito, você libera sua mente para focar nos aspectos mais complexos e interessantes da matemática, construindo uma base sólida para enfrentar desafios maiores, seja na matemática universitária, na preparação para concursos ou no aprofundamento dos estudos no ensino médio.

Parte 2: Ajustando a Rota – Como Seus Hábitos Podem Estar Sabotando Seu Aprendizado

Tão importante quanto dominar as regras e técnicas matemáticas é a forma como você aborda o estudo. Muitas vezes, a dificuldade em matemática não reside apenas nos conceitos em si, mas em estratégias de estudo ineficazes ou contraproducentes. São armadilhas comportamentais e metodológicas que podem minar sua confiança, desperdiçar seu tempo e impedir que você realmente consiga aprender matemática de forma sólida e duradoura. Vamos analisar os erros de estratégia mais comuns que afetam estudantes do ensino médio, universitários e concurseiros, e como ajustar sua rota para um aprendizado mais eficiente.

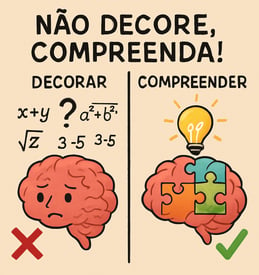
Erro 8: Decorar vs. Compreender – A Ilusão da Memorização Pura

Um dos maiores equívocos ao estudar matemática é tratar a disciplina como um conjunto de fórmulas e procedimentos a serem simplesmente memorizados. Decorar a fórmula de Bhaskara ou os passos para resolver um sistema linear pode até funcionar para uma prova específica sobre aquele tópico isolado, mas essa abordagem é superficial e insustentável a longo prazo.

A Armadilha: O estudante decora a fórmula a² = b² + c² mas não entende que ela se aplica apenas a triângulos retângulos e representa a relação entre os catetos e a hipotenusa. Diante de um problema ligeiramente diferente ou que exige a aplicação do conceito em um contexto novo, a fórmula decorada se torna inútil.

A Consequência: Incapacidade de resolver problemas que fogem do padrão exato dos exemplos vistos, dificuldade em conectar diferentes áreas da matemática, fragilidade no conhecimento que desmorona diante de tópicos mais avançados que dependem daquela base.

Como Evitar:

•Foque no "Porquê": Não se contente em saber como fazer, pergunte-se por que funciona assim. Qual a lógica por trás da fórmula? De onde ela vem?

•Busque Demonstrações: Entender a demonstração de um teorema ou fórmula (mesmo que de forma simplificada) ajuda a internalizar o conceito.

•Conecte Conceitos: Veja como diferentes tópicos se relacionam. Como a álgebra se conecta com a geometria? Como as funções descrevem fenômenos do mundo real?

•Ensine para Alguém: Explicar um conceito com suas próprias palavras para um colega (ou mesmo para si mesmo em voz alta) é um teste poderoso de compreensão.

•Visualize: Use gráficos, diagramas ou exemplos concretos para tornar os conceitos abstratos mais tangíveis.

Erro 9: Prática Insuficiente ou Monótona – O Perigo da Repetição sem Variação

A matemática é uma habilidade que, como tocar um instrumento musical ou praticar um esporte, exige prática constante. No entanto, não basta apenas fazer exercícios; a qualidade e a variedade da prática são fundamentais.

A Armadilha: O estudante resolve dezenas de vezes o mesmo tipo de equação quadrática, usando sempre a fórmula de Bhaskara, mas evita problemas que envolvam interpretação, contextualização ou que possam ser resolvidos por outros métodos (como soma e produto ou completar quadrados).

A Consequência: O estudante se torna bom em aplicar mecanicamente um procedimento específico, mas não desenvolve a flexibilidade de raciocínio necessária para escolher a melhor abordagem para cada problema ou para enfrentar questões que exigem mais interpretação e criatividade. Falta fluência e adaptabilidade.

Como Evitar:

•Volume e Variedade: Resolva um número significativo de exercícios, mas busque variedade. Procure problemas com diferentes níveis de dificuldade, enunciados diversos, contextos de aplicação variados e que explorem o mesmo conceito sob ângulos distintos.

•Saia da Zona de Conforto: Não fuja dos problemas mais desafiadores. São eles que realmente esticam seu raciocínio e consolidam o aprendizado.

•Explore Métodos Alternativos: Mesmo que você domine um método, tente resolver o mesmo problema usando outras abordagens. Isso aprofunda sua compreensão e amplia seu repertório de ferramentas.

•Use Fontes Diversas: Não se limite ao livro didático. Busque listas de exercícios online, provas antigas (ENEM, vestibulares, concursos), desafios matemáticos.

Erro 10: O Medo de Perguntar – Deixando Dúvidas Virarem Lacunas

A dúvida é parte intrínseca do processo de aprendizagem, especialmente em uma disciplina como a matemática. No entanto, muitos estudantes sentem vergonha, receio de parecerem "burros" ou simplesmente não querem interromper a aula ou incomodar o professor/colegas, e acabam guardando suas dúvidas.

A Armadilha: O estudante não entende um passo na resolução de um problema sobre logaritmos, mas não pergunta. Na aula seguinte, o professor usa aquele conceito como base para explicar propriedades mais avançadas. A dúvida inicial não resolvida impede a compreensão do novo conteúdo, criando um efeito bola de neve.

A Consequência: Pequenas dúvidas se transformam em grandes lacunas no conhecimento. A base fica comprometida, dificultando o aprendizado de tópicos futuros que dependem dos anteriores. A frustração aumenta, reforçando a ideia de que "matemática não é para mim".

Como Evitar:

•Encare a Dúvida como Aliada: Entenda que perguntar não é sinal de fraqueza, mas de engajamento e desejo de aprender.

•Anote Imediatamente: Assim que uma dúvida surgir, anote-a. Não confie na memória.

•Seja Específico: Ao perguntar, tente formular sua dúvida da forma mais clara possível. "Não entendi nada" é menos útil do que "Não entendi por que, neste passo, o expoente passou a multiplicar o logaritmo".

•Busque Ajuda Ativamente: Não espere! Pergunte ao professor ao final da aula, procure monitores, forme grupos de estudo com colegas, utilize fóruns online dedicados à matemática. Existem muitos recursos disponíveis.

Erro 11: Estudar na Véspera – O 'Cramming' Improdutivo e Estressante

Deixar para estudar todo o conteúdo de matemática na noite anterior à prova (o famoso cramming) é uma das estratégias de estudo mais ineficazes e prejudiciais.

A Armadilha: O estudante passa a madrugada tentando absorver semanas ou meses de conteúdo, focando na memorização de curto prazo para "passar na prova".

A Consequência: O aprendizado é superficial e volátil. O conteúdo é rapidamente esquecido após a prova, não havendo retenção a longo prazo. Além disso, essa prática gera altos níveis de estresse e ansiedade, o que pode prejudicar o desempenho na hora H, mesmo que o estudante tenha conseguido decorar algo.

Como Evitar:

•Estudo Regular e Distribuído: A matemática exige construção gradual de conhecimento. Estude um pouco a cada dia ou algumas vezes por semana, de forma consistente.

•Revisão Espaçada: Não basta aprender um tópico uma vez. Revise-o periodicamente em intervalos crescentes (um dia depois, uma semana depois, um mês depois). Isso fortalece a memória de longo prazo.

•Crie um Cronograma: Planeje seus estudos. Defina metas realistas de quais tópicos revisar ou praticar a cada semana.

•Durma Bem: O sono é crucial para a consolidação da memória e do aprendizado. Virar a noite estudando é contraproducente.

Erro 12: Ignorar a Base – Construindo um Arranha-Céu em Terreno Frágil

Muitos estudantes, ansiosos por chegar aos tópicos mais "avançados" ou relevantes para suas provas (especialmente concurseiros e universitários), negligenciam a importância de ter uma base sólida em matemática básica (operações aritméticas, frações, porcentagem, regras de sinais, resolução de equações simples).

A Armadilha: O estudante tenta aprender cálculo diferencial e integral sem ter um domínio seguro de funções, limites ou mesmo manipulação algébrica básica.

A consequência: A dificuldade se torna exponencial. Cada novo conceito parece impossível de entender porque as ferramentas básicas necessárias para manipulá-lo não estão afiadas. Isso gera frustração, perda de tempo e a sensação de estar "patinando" sem sair do lugar.

Como Evitar:

•Diagnóstico Honesto: Faça uma autoavaliação sincera ou peça ajuda a um professor para identificar suas fraquezas na matemática básica.

•Não Tenha Vergonha de Voltar: Se necessário, reserve um tempo para revisar e praticar os fundamentos. Invista em fortalecer sua base. Livros e materiais de ensino médio podem ser muito úteis aqui, mesmo para universitários.

•Construa Gradualmente: Certifique-se de que você realmente domina um pré-requisito antes de avançar para o próximo tópico.

Erro 13: Falta de Revisão Sistemática – O Conhecimento que Escorre Pelos Dedos

O cérebro humano tende a esquecer informações que não são utilizadas ou revisitadas. Aprender um tópico de matemática uma única vez, mesmo que com compreensão, não garante que ele estará disponível na sua memória quando você precisar dele semanas ou meses depois.

A Armadilha: O estudante aprendeu bem sobre matrizes no início do semestre, mas nunca mais revisou o assunto. Meses depois, em um tópico de álgebra linear avançada ou em uma questão de concurso que envolve matrizes, ele percebe que esqueceu detalhes importantes ou como realizar certas operações.

A Consequência: Perda de tempo tendo que reaprender conteúdos, dificuldade em conectar tópicos que dependem de conhecimentos anteriores, desempenho inferior em avaliações cumulativas.

Como Evitar:

•Implemente a Revisão Espaçada: Use aplicativos, planilhas ou um sistema manual para agendar revisões periódicas dos tópicos estudados.

•Resolva Problemas Antigos: Regularmente, refaça exercícios de tópicos anteriores para manter o conhecimento ativo.

•Faça Mapas Mentais ou Resumos: Criar seus próprios materiais de revisão ajuda na consolidação e facilita a consulta rápida.

•Integre Conhecimentos: Ao aprender um novo tópico, tente conectá-lo com o que você já sabe. Como isso se relaciona com...? Onde mais eu posso aplicar isso?

Erro 14: Mentalidade Fixa e Ansiedade Matemática – As Barreiras Invisíveis

Talvez a armadilha mais sutil, porém poderosa, seja a mentalidade com a qual se encara a matemática. Acreditar que a habilidade matemática é um dom inato ("ou você nasce bom nisso, ou não é para você" – mentalidade fixa) ou desenvolver um medo e bloqueio paralisantes diante da disciplina (ansiedade matemática) são barreiras enormes para o aprendizado.

A Armadilha: O estudante erra um problema e pensa: "Eu sou péssimo em matemática, nunca vou aprender". Diante de um desafio, ele sente o coração acelerar, a mente fica em branco e ele evita a tarefa ou desiste facilmente.

A Consequência: Profecia autorrealizável – a crença na própria incapacidade leva à falta de esforço ou a estratégias de evitação, o que resulta em baixo desempenho, reforçando a crença inicial. A ansiedade impede o raciocínio claro e a aplicação do conhecimento que o estudante até possui.

Como Evitar:

•Cultive a Mentalidade de Crescimento: Entenda que a habilidade matemática, como qualquer outra, se desenvolve com esforço, prática e estratégias eficazes. Erros são oportunidades de aprendizado, não sentenças de incapacidade.

•Foco no Processo, Não Apenas no Resultado: Valorize o esforço, a persistência e as estratégias que você utiliza, não apenas se acertou ou errou a resposta final.

•Celebre Pequenas Vitórias: Reconheça e comemore seu progresso, por menor que pareça. Conseguiu entender um conceito que antes era difícil? Resolveu um problema desafiador? Isso importa!

•Desmistifique a Matemática: Procure ver a matemática em contextos interessantes, em jogos, na natureza, na arte. Isso pode reduzir a percepção de que ela é apenas uma matéria escolar árida.

•Técnicas de Relaxamento: Se a ansiedade for um problema significativo, técnicas de respiração profunda, mindfulness ou buscar apoio psicológico podem ajudar a gerenciar as reações físicas e mentais.

Superar essas armadilhas na estratégia de estudo exige autoconsciência e disposição para mudar hábitos. Ao adotar uma abordagem mais focada na compreensão, na prática variada e consistente, na busca ativa por ajuda e no cultivo de uma mentalidade positiva, você estará pavimentando um caminho muito mais eficaz e gratificante para aprender matemática e alcançar seus objetivos, seja no ensino médio, na universidade ou em concursos.

Parte 3: Estratégias Sob Medida – Otimizando Seus Estudos para Cada Fase

Embora os erros técnicos e as armadilhas de estudo sejam comuns a muitos, as necessidades e os desafios específicos podem variar dependendo da sua fase de aprendizado. Um estudante do ensino médio tem prioridades diferentes de um universitário que lida com cálculo avançado, que por sua vez difere de um concurseiro focado em resolver questões rapidamente sob pressão. Reconhecer essas nuances e adaptar suas estratégias de estudo em matemática pode fazer uma grande diferença no seu desempenho. Vamos explorar algumas dicas direcionadas para cada um desses perfis.

Para Estudantes do Ensino Médio: Construindo a Base para o Futuro

O ensino médio é uma fase crucial para consolidar a matemática básica e construir os alicerces para desafios futuros, como o ENEM, vestibulares e o próprio ensino superior. O foco aqui deve ser tanto na compreensão dos conceitos quanto na aplicação prática.

•Solidifique a Base: Não subestime a importância dos fundamentos. Dedique tempo para garantir que operações básicas, frações, porcentagens, álgebra elementar e geometria plana estejam bem compreendidos. Use essa fase para preencher quaisquer lacunas que possam ter ficado do ensino fundamental. Revisitar esses tópicos é um investimento, não uma perda de tempo.

•Conecte com o Cotidiano: A matemática do ensino médio está repleta de aplicações práticas. Busque entender como funções modelam situações reais, como a geometria se aplica à arquitetura ou ao design, como a probabilidade aparece em jogos e estatísticas. Tornar a matemática relevante para o seu mundo torna o aprendizado mais significativo e menos abstrato.

•Visualize Conceitos: Use gráficos, softwares de geometria dinâmica (como GeoGebra), ou mesmo desenhos para visualizar conceitos abstratos como funções, vetores ou sólidos geométricos. A visualização ajuda na intuição e na compreensão.

•Pratique com Provas Anteriores: Familiarize-se com o estilo das questões do ENEM e dos vestibulares que você pretende prestar. Resolver provas antigas ajuda a entender os tópicos mais cobrados, o nível de dificuldade esperado e a gerenciar o tempo.

•Desenvolva o Raciocínio Lógico: Muitos problemas do ensino médio, especialmente no ENEM, exigem mais interpretação e raciocínio lógico do que a aplicação direta de fórmulas complexas. Pratique a leitura atenta dos enunciados e a construção de linhas de raciocínio consistentes.

Para Universitários: Navegando na Abstração e no Rigor

A matemática universitária frequentemente introduz um nível maior de abstração, rigor formal e complexidade. Cálculo, Álgebra Linear, Probabilidade e Estatística Avançada exigem não apenas a capacidade de calcular, mas também de entender demonstrações, trabalhar com definições precisas e aplicar conceitos em contextos específicos da área de estudo (Engenharia, Economia, Física, Computação, etc.).

•Abrace o Rigor: Entenda que definições precisas, teoremas e demonstrações são a espinha dorsal da matemática em nível superior. Dedique tempo para compreendê-los, mesmo que não sejam diretamente cobrados em todas as avaliações. Eles constroem a base para o entendimento profundo.

•Gerencie o Tempo: A carga de estudos na universidade costuma ser alta, com diversas disciplinas competindo por sua atenção. Crie um cronograma de estudos realista, distribuindo o tempo dedicado à matemática ao longo da semana, e não deixando acumular.

•Busque Conexões com sua Área: Entenda como a matemática que você está aprendendo se aplica à sua futura profissão. Como o cálculo é usado para modelar fenômenos na engenharia? Como a álgebra linear é fundamental em computação gráfica ou análise de dados? Essa conexão aumenta a motivação e a relevância do estudo.

•Aproveite Recursos da Universidade: Monitorias, grupos de estudo orientados por veteranos ou professores, bibliotecas com vasto acervo – utilize todos os recursos que sua instituição oferece. Discutir problemas com colegas e monitores pode trazer novas perspectivas.

•Não Pule Pré-requisitos: Certifique-se de que você domina os conceitos de disciplinas anteriores que são base para as atuais. Se está cursando Cálculo II, garanta que seu Cálculo I e sua base de funções e álgebra estão sólidos.

Para Concurseiros: Eficiência, Estratégia e Foco na Banca

Para quem estuda matemática para concursos, o objetivo principal é acertar o maior número de questões possível, geralmente dentro de um tempo limitado. A eficiência, a estratégia e o conhecimento do estilo da banca examinadora são cruciais.

•Agilidade e Eficiência: O tempo é um fator crítico. Pratique resolver questões não apenas corretamente, mas também rapidamente. Desenvolva "macetes" e atalhos válidos (sem comprometer a compreensão), identifique padrões e aprenda a estimar resultados quando apropriado.

•Conheça a Banca: Cada banca organizadora de concurso tem seu estilo próprio, tópicos preferidos e nível de profundidade. Analise editais e provas anteriores da banca específica do seu concurso para direcionar seus estudos aos conteúdos mais relevantes e ao formato de questão esperado.

•Foco nos Tópicos de Maior Incidência: Analise a frequência com que cada tópico de matemática costuma cair nas provas do seu concurso e priorize aqueles de maior incidência e/ou que valem mais pontos, sem negligenciar completamente os demais.

•Simule as Condições de Prova: Resolva simulados completos, cronometrando o tempo e tentando reproduzir as condições do dia da prova (pressão, ambiente). Isso ajuda a gerenciar o tempo e a controlar a ansiedade.

•Revisão Estratégica: Mantenha um caderno de erros ou um resumo dos pontos onde você tem mais dificuldade e revise-os com frequência. Foque em entender por que errou e como evitar o mesmo erro no futuro.

•Interpretação de Enunciado: Muitas questões de concurso testam a capacidade de interpretação tanto quanto o conhecimento matemático. Pratique ler atentamente os enunciados, identificar os dados relevantes e o que realmente está sendo pedido.

Independentemente da sua fase, lembre-se que aprender matemática é um processo contínuo. Adaptar suas estratégias às suas necessidades específicas, combinado com a correção dos erros técnicos e a superação das armadilhas de estudo discutidas anteriormente, irá potencializar seu aprendizado e aproximá-lo dos seus objetivos.

Conclusão: Transformando Erros em Degraus para o Sucesso

Chegamos ao final da nossa jornada pelos erros comuns ao estudar matemática. Vimos que os tropeços vão desde falhas técnicas em cálculos básicos, como a ordem das operações ou a manipulação de sinais, até armadilhas mais sutis relacionadas às nossas estratégias de estudo e à nossa própria mentalidade em relação à disciplina. Seja você um estudante do ensino médio buscando uma base sólida, um universitário enfrentando conceitos abstratos ou um concurseiro lutando contra o relógio, a mensagem central é a mesma: errar faz parte do processo, mas persistir no erro por falta de conhecimento ou estratégia é um obstáculo que pode – e deve – ser superado.

A chave para aprender matemática de forma eficaz não está em nunca cometer erros, mas em reconhecê-los, entender suas causas e implementar ativamente as estratégias para evitá-los no futuro. Trata-se de trocar a memorização superficial pela compreensão profunda, a prática monótona pela resolução variada de problemas, o medo de perguntar pela busca ativa por ajuda, e a mentalidade fixa pela crença de que sua capacidade pode, sim, ser desenvolvida com esforço e dedicação.

Esperamos que este guia detalhado sirva como um mapa para identificar seus próprios pontos fracos e como um conjunto de ferramentas para ajustar sua rota de estudos. Lembre-se: a dificuldade em matemática muitas vezes é apenas um sinal de que a abordagem precisa ser diferente. Com paciência, persistência e as estratégias certas, você pode transformar a frustração em confiança e os desafios em conquistas.

Agora é com você! Coloque essas dicas em prática, observe seus hábitos de estudo e não hesite em revisitar este material sempre que precisar. A matemática pode ser desafiadora, mas também incrivelmente recompensadora quando desvendada.

Gostou deste conteúdo? Tem alguma outra dica ou erro comum que gostaria de compartilhar? Deixe seu comentário abaixo! E não se esqueça de explorar outros artigos e recursos aqui no Nossa Matemática para continuar aprimorando seus conhecimentos.