Equação do Segundo Grau Desmistificada

1. Introdução: Decifrando um Enigma Matemático

Você já se deparou com problemas que parecem exigir uma solução mais elaborada do que uma simples conta de adição ou subtração? Situações onde as relações entre as quantidades não são lineares, mas sim curvas, como a trajetória de uma bola lançada ao ar ou o cálculo da área máxima de um terreno com uma cerca de tamanho fixo? Bem-vindo ao fascinante mundo da Equação do Segundo Grau!

Pode parecer um nome intimidante à primeira vista, mas a equação do segundo grau é uma ferramenta matemática poderosa e surpreendentemente presente em nosso dia a dia e em diversas áreas do conhecimento, como física, engenharia, economia e, claro, na própria matemática. Ela nos ajuda a modelar e resolver uma vasta gama de problemas que envolvem relações quadráticas.

Neste guia completo, preparado especialmente para estudantes do ensino fundamental, vamos desmistificar a equação do segundo grau passo a passo. Nosso objetivo é tornar esse tema acessível e interessante, mostrando que, com as ferramentas certas e um pouco de prática, qualquer um pode dominar esse conceito fundamental. Exploraremos desde a sua definição básica e a identificação de seus componentes até os métodos de resolução, incluindo a famosa Fórmula de Bhaskara, a análise de suas raízes, sua representação gráfica através de parábolas e suas aplicações práticas.

Prepare-se para embarcar nesta jornada de descoberta matemática! Ao final deste artigo, você terá uma compreensão sólida sobre as equações do segundo grau e estará mais confiante para aplicá-las em seus estudos e na resolução de problemas. Vamos começar?

2. Definindo a Equação do Segundo Grau: A Forma Geral e Seus Componentes

Para começar, precisamos entender o que exatamente define uma equação do segundo grau. Formalmente, uma equação do segundo grau na incógnita x é qualquer equação que pode ser escrita na seguinte forma geral:

ax² + bx + c = 0

Onde:

• x é a incógnita (o valor que queremos descobrir).

• a, b e c são números reais chamados coeficientes da equação.

• A condição mais importante é que o coeficiente a deve ser diferente de zero (a ≠ 0). Se a fosse igual a zero, o termo ax² desapareceria, e a equação se tornaria uma equação do primeiro grau (bx + c = 0), que já conhecemos.

Vamos analisar cada termo e coeficiente com mais detalhe:

• ax²: Este é o termo quadrático. É ele que caracteriza a equação como sendo do segundo grau, pois a incógnita x está elevada ao expoente 2. O coeficiente a acompanha este termo.

• bx: Este é o termo linear. A incógnita x está elevada ao expoente 1 (que geralmente não escrevemos). O coeficiente b acompanha este termo.

• c: Este é o termo independente ou constante. Ele não acompanha a incógnita x.

Identificando os Coeficientes (a, b, c): A Chave para Começar

Saber identificar corretamente os coeficientes a, b e c é o primeiro e crucial passo para resolver qualquer equação do segundo grau. Vamos ver alguns exemplos:

• Exemplo 1: 2x² + 5x - 3 = 0

  • a = 2 (coeficiente de x²)

  • b = 5 (coeficiente de x)

  • c = -3 (termo independente)

• Exemplo 2: x² - 7x + 10 = 0

  • a = 1 (quando não há número visível antes de x², o coeficiente é 1)

  • b = -7 (atenção ao sinal negativo)

  • c = 10

• Exemplo 3: -3x² + 9 = 0

  • a = -3

  • b = 0 (não há termo com x elevado a 1, então b = 0)

  • c = 9

• Exemplo 4: 4x² - 8x = 0

  • a = 4

  • b = -8

  • c = 0 (não há termo independente, então c = 0)

• Exemplo 5: 5x² = 0

  • a = 5

  • b = 0

  • c = 0

Perceba que, mesmo quando alguns termos parecem faltar, a equação ainda pode ser do segundo grau, desde que a seja diferente de zero. Os coeficientes b e c, no entanto, podem ser iguais a zero, como veremos a seguir.

3. Tipos de Equações do Segundo Grau: Completas e Incompletas

Nem todas as equações do segundo grau aparecem na forma completa ax² + bx + c = 0. Dependendo dos valores dos coeficientes b e c, podemos classificá-las em completas ou incompletas. Reconhecer esses tipos é útil, pois as equações incompletas geralmente possuem métodos de resolução mais simples e rápidos do que a aplicação da fórmula geral.

Equações Completas

Uma equação do segundo grau é considerada completa quando todos os seus coeficientes são diferentes de zero (a ≠ 0, b ≠ 0 e c ≠ 0).

• Exemplos:

  • 3x² - 7x + 2 = 0 (a=3, b=-7, c=2)

  • x² + x + 1 = 0 (a=1, b=1, c=1)

  • -2x² + 5x - 1 = 0 (a=-2, b=5, c=-1)

Para resolver equações completas, geralmente utilizamos a Fórmula de Bhaskara, que veremos em detalhes na próxima seção.

Equações Incompletas

Uma equação do segundo grau é incompleta quando o coeficiente b ou o coeficiente c (ou ambos) são iguais a zero. Lembre-se, a nunca pode ser zero!

Existem três casos de equações incompletas:

• Caso 1: b = 0 (Forma ax² + c = 0) Neste caso, falta o termo linear (bx). A equação tem a forma ax² + c = 0.

  • Método de Resolução: Isolamos o termo x² e extraímos a raiz quadrada.

    1. Passe o termo c para o outro lado da igualdade: ax² = -c

    2. Passe o coeficiente a dividindo: x² = -c/a

    3. Extraia a raiz quadrada de ambos os lados: x = ±√(-c/a) Importante: Só haverá raízes reais se o valor dentro da raiz quadrada (-c/a) for não negativo (maior ou igual a zero).

  • Exemplo: Resolver 3x² - 27 = 0

    1. 3x² = 27

    2. x² = 27 / 3

    3. x² = 9

    4. x = ±√9

    5. x = +3 ou x = -3. As raízes são 3 e -3.

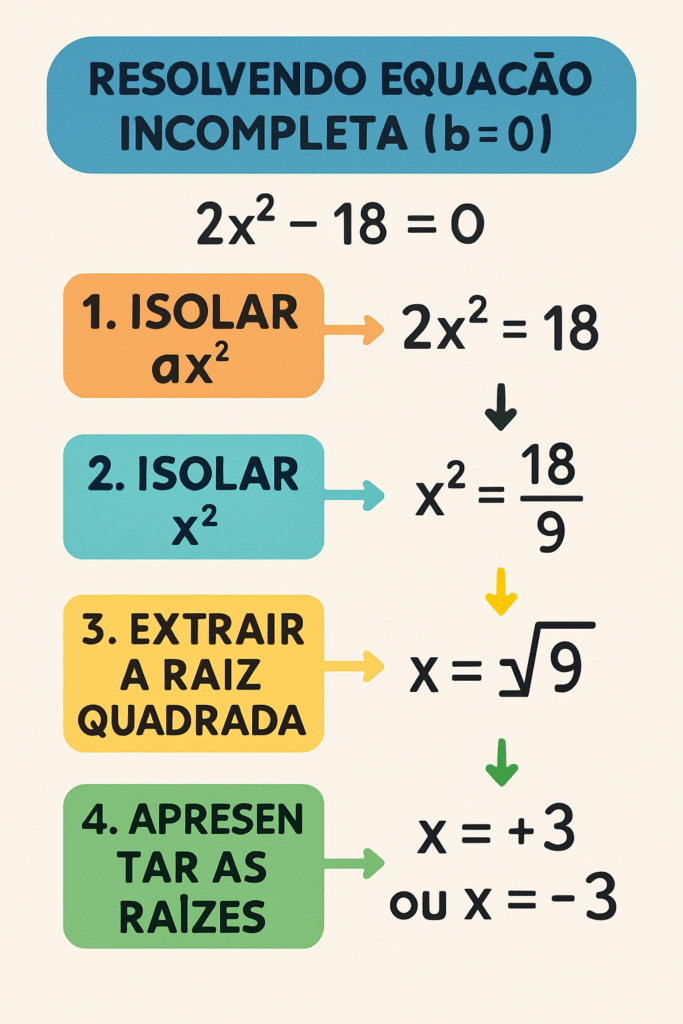
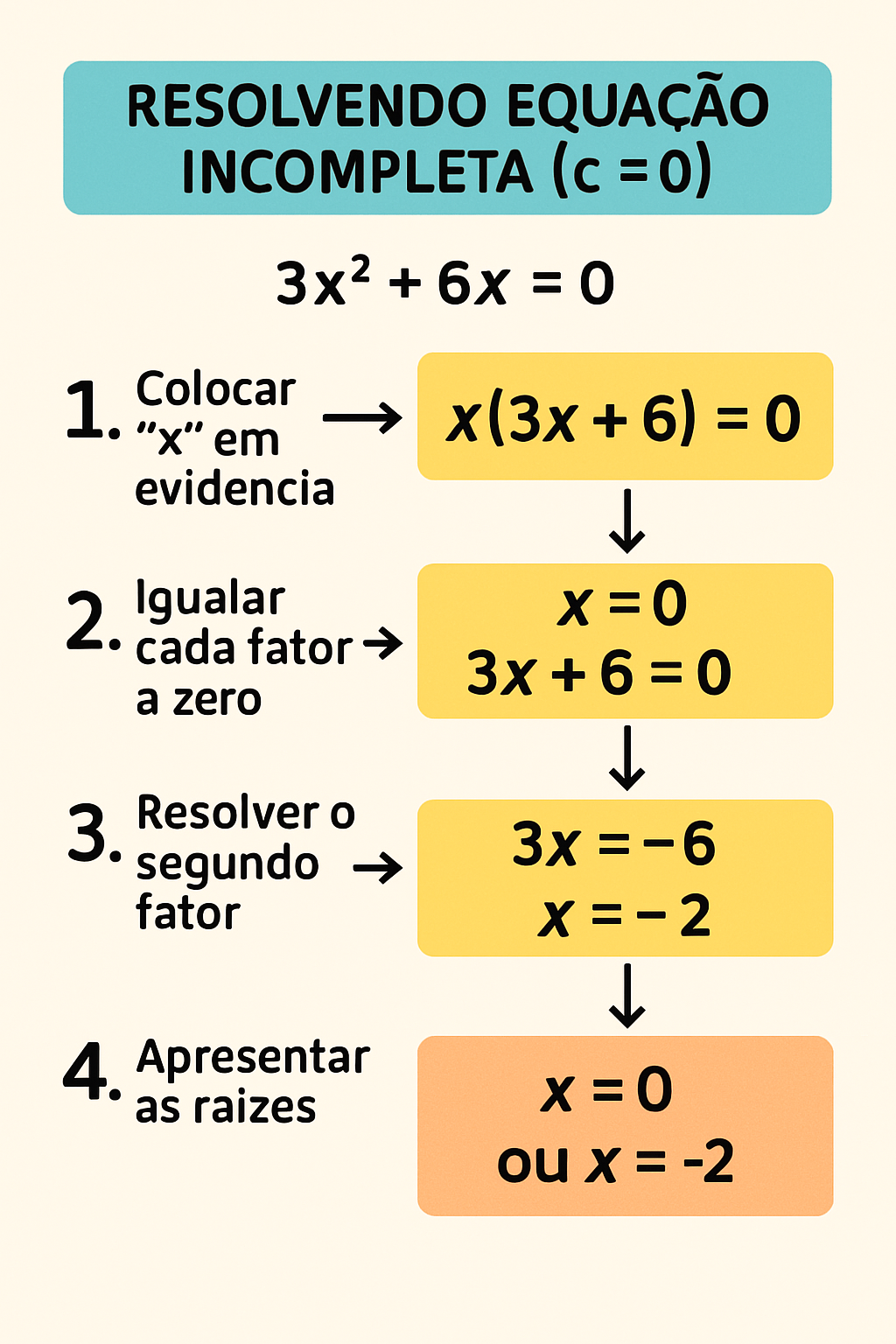
• Caso 2: c = 0 (Forma ax² + bx = 0) Neste caso, falta o termo independente (c). A equação tem a forma ax² + bx = 0.

  • Método de Resolução: Fatoração, colocando o fator comum x em evidência.

    1. Coloque x em evidência: x(ax + b) = 0

    2. Para que um produto seja zero, um dos fatores deve ser zero. Portanto, temos duas possibilidades:

       • x = 0 (esta é sempre uma das raízes quando c = 0)

       • ax + b = 0 => ax = -b => x = -b/a (esta é a outra raiz)

  • Exemplo: Resolver 2x² + 8x = 0

    1. x(2x + 8) = 0

    2. Possibilidades:

       • x = 0

       • 2x + 8 = 0 => 2x = -8 => x = -8 / 2 => x = -4

    3. As raízes são 0 e -4.

• Caso 3: b = 0 e c = 0 (Forma ax² = 0) Este é o caso mais simples, onde faltam tanto o termo linear quanto o termo independente.

  • Método de Resolução:

    1. ax² = 0

    2. Como a ≠ 0, a única possibilidade é x² = 0.

    3. Extraindo a raiz quadrada, temos x = 0.

  • Solução: A equação ax² = 0 sempre terá duas raízes reais iguais a zero (ou uma raiz dupla igual a zero).

  • Exemplo: Resolver -5x² = 0

    1. x² = 0 / -5

    2. x² = 0

    3. x = 0. A raiz dupla é 0.

Reconhecer e saber resolver rapidamente as equações incompletas economiza tempo e esforço. No entanto, para as equações completas, precisamos de uma ferramenta mais robusta: a Fórmula de Bhaskara.

4. A Fórmula Resolutiva: Bhaskara ao Resgate! (A Solução Geral)

Quando nos deparamos com uma equação do segundo grau completa (ax² + bx + c = 0, com a, b, c ≠ 0), os métodos de isolar x ou fatorar diretamente não são tão simples. Foi para resolver este tipo de equação (e também as incompletas, embora não seja o método mais rápido para elas) que foi desenvolvida uma fórmula geral, conhecida no Brasil como Fórmula de Bhaskara.

Embora a autoria histórica da fórmula seja debatida e atribuída a outros matemáticos antes de Bhaskara II, ela é universalmente utilizada para encontrar as raízes de qualquer equação do segundo grau.

A fórmula é a seguinte:

x = [-b ± √(b² - 4ac)] / 2a

Vamos analisar cada parte:

• -b: O oposto do coeficiente b.

• ±: O símbolo "mais ou menos" indica que teremos duas possíveis soluções, uma usando o sinal de mais e outra usando o sinal de menos.

• √(b² - 4ac): A raiz quadrada de uma expressão muito importante chamada Discriminante.

• 2a: O dobro do coeficiente a.

O Coração da Fórmula: O Discriminante (Delta - Δ)

A expressão dentro da raiz quadrada, b² - 4ac, é fundamental e recebe um nome especial: Discriminante, representado pela letra grega Delta (Δ).

Δ = b² - 4ac

O valor do discriminante Δ é crucial porque ele nos diz quantas raízes reais a equação possui, antes mesmo de calcularmos essas raízes. Como estamos extraindo a raiz quadrada de Δ (√Δ) na fórmula de Bhaskara, o sinal de Δ determina a natureza das soluções:

• Se Δ > 0, a raiz quadrada √Δ será um número real positivo. A fórmula de Bhaskara fornecerá duas raízes reais e diferentes (uma com +√Δ e outra com -√Δ).

• Se Δ = 0, a raiz quadrada √Δ será zero. A fórmula de Bhaskara fornecerá duas raízes reais e iguais (ou uma raiz dupla), pois somar ou subtrair zero não altera o resultado: x = -b / 2a.

• Se Δ < 0, a raiz quadrada √Δ não será um número real (não existe raiz quadrada real de número negativo). Neste caso, a equação não possui raízes reais.

Veremos mais sobre a análise do discriminante na próxima seção.

Aplicando a Fórmula de Bhaskara: Passo a Passo

Resolver uma equação do segundo grau usando a fórmula de Bhaskara envolve um processo sistemático:

1. Identificar os Coeficientes: Determine os valores de a, b e c na equação ax² + bx + c = 0.

2. Calcular o Discriminante (Δ): Use a fórmula Δ = b² - 4ac.

3. Analisar o Discriminante: Verifique se Δ é positivo, zero ou negativo para saber quantas raízes reais esperar.

4. Aplicar a Fórmula de Bhaskara: Substitua os valores de a, b e Δ na fórmula x = [-b ± √Δ] / 2a.

5. Calcular as Raízes: Encontre os dois valores de x (x₁ e x₂), um usando +√Δ e outro usando -√Δ (se Δ ≥ 0).

Exemplo Resolvido Detalhadamente: Resolver a equação x² - 5x + 6 = 0

1. Identificar Coeficientes: a = 1, b = -5, c = 6.

2. Calcular Discriminante (Δ): Δ = b² - 4ac Δ = (-5)² - 4 (1) (6) Δ = 25 - 24 Δ = 1

3. Analisar Discriminante: Como Δ = 1 (Δ > 0), esperamos duas raízes reais e distintas.

4. Aplicar Fórmula de Bhaskara: x = [-b ± √Δ] / 2a x = [-(-5) ± √1] / (2 * 1) x = [5 ± 1] / 2

5. Calcular as Raízes:

   • x₁ = (5 + 1) / 2 = 6 / 2 = 3

   • x₂ = (5 - 1) / 2 = 4 / 2 = 2

Resposta: As raízes da equação x² - 5x + 6 = 0 são x₁ = 3 e x₂ = 2.

Outro Exemplo: Resolver a equação 4x² - 4x + 1 = 0

1. Coeficientes: a = 4, b = -4, c = 1.

2. Discriminante (Δ): Δ = (-4)² - 4 (4) (1) Δ = 16 - 16 Δ = 0

3. Análise: Como Δ = 0, esperamos uma raiz real dupla.

4. Bhaskara: x = [-(-4) ± √0] / (2 * 4) x = [4 ± 0] / 8

5. Raízes:

   • x₁ = (4 + 0) / 8 = 4 / 8 = 1/2

   • x₂ = (4 - 0) / 8 = 4 / 8 = 1/2

Resposta: A equação possui uma raiz real dupla x = 1/2.

Mais um Exemplo: Resolver a equação x² + 2x + 5 = 0

1. Coeficientes: a = 1, b = 2, c = 5.

2. Discriminante (Δ): Δ = (2)² - 4 (1) (5) Δ = 4 - 20 Δ = -16

3. Análise: Como Δ = -16 (Δ < 0), a equação não possui raízes reais.

Resposta: A equação não possui solução no conjunto dos números reais.

A Fórmula de Bhaskara é, portanto, uma ferramenta completa para encontrar as soluções de qualquer equação do segundo grau, e a análise prévia do discriminante Δ nos dá informações valiosas sobre a natureza dessas soluções.

5. Analisando o Discriminante (Δ): O Que Ele Nos Conta Sobre as Raízes?

Como vimos, o discriminante Δ = b² - 4ac é mais do que apenas uma parte da Fórmula de Bhaskara; ele é um indicador poderoso sobre as soluções (raízes) da equação do segundo grau ax² + bx + c = 0, especificamente no conjunto dos números reais.

Compreender o significado do sinal do discriminante nos permite antecipar o tipo de solução que encontraremos, economizando tempo e ajudando na interpretação gráfica da equação.

Vamos aprofundar a análise de cada caso:

• Caso 1: Δ > 0 (Discriminante Positivo)

  • Significado Matemático: Quando Δ é positivo, a raiz quadrada de Δ (√Δ) é um número real positivo. Na fórmula de Bhaskara, x = [-b ± √Δ] / 2a, ao somar e subtrair √Δ de -b, obteremos dois resultados diferentes para x.

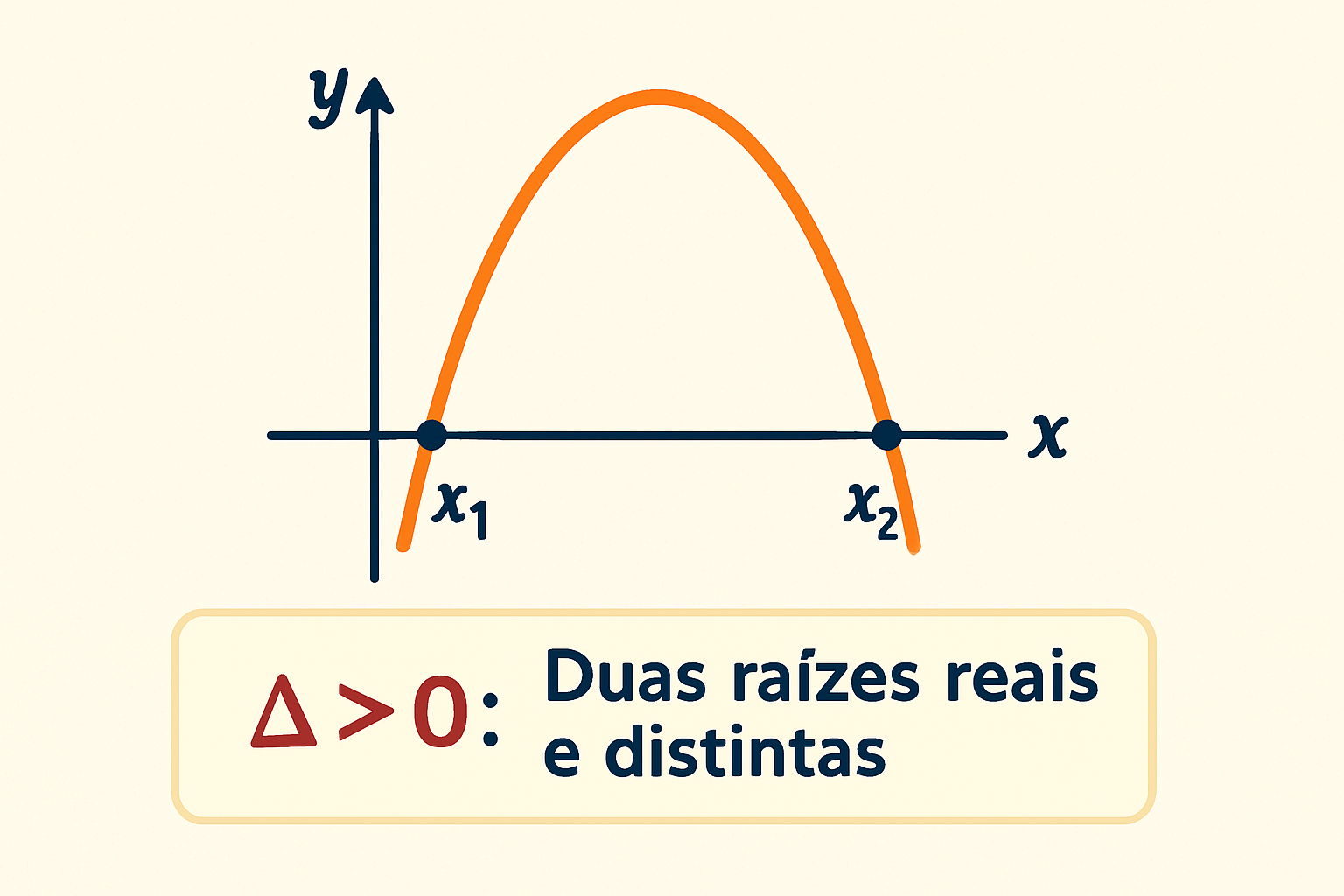
  • Conclusão: A equação possui duas raízes reais e distintas (diferentes uma da outra).

  • Exemplo: Vimos que para x² - 5x + 6 = 0, Δ = 1 (positivo). As raízes encontradas foram x₁ = 3 e x₂ = 2, que são dois números reais distintos.

  • Interpretação Gráfica: A parábola que representa a função y = ax² + bx + c corta o eixo x em dois pontos distintos. Esses pontos de interseção correspondem exatamente às duas raízes reais da equação.

• Caso 2: Δ = 0 (Discriminante Nulo)

  • Significado Matemático: Quando Δ é zero, a raiz quadrada de Δ (√Δ) é zero. Na fórmula de Bhaskara, x = [-b ± √0] / 2a, somar ou subtrair zero não altera o valor de -b. Portanto, as duas possíveis soluções se tornam idênticas.

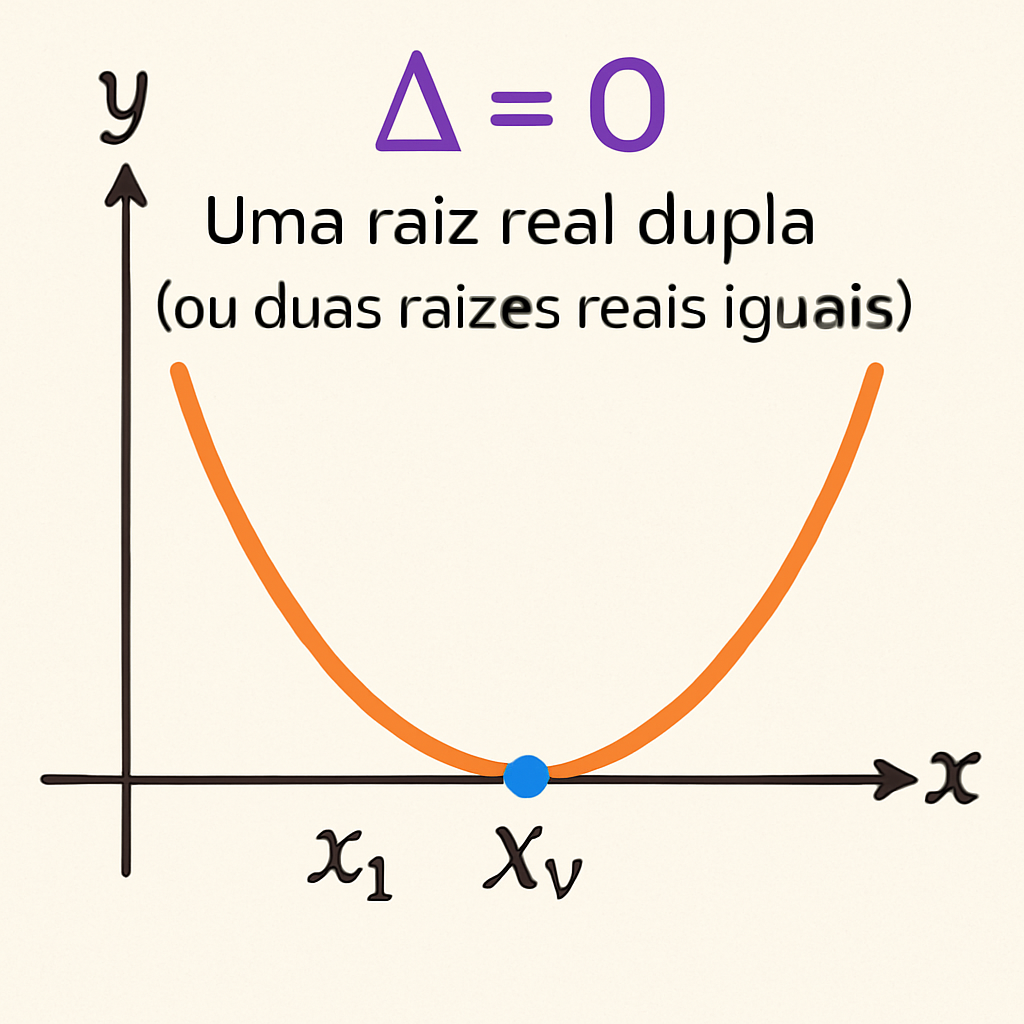
  • Conclusão: A equação possui duas raízes reais e iguais, ou, como é mais comum dizer, uma raiz real dupla.

  • Exemplo: Vimos que para 4x² - 4x + 1 = 0, Δ = 0. A raiz encontrada foi x = 1/2 (considerada uma raiz dupla).

  • Interpretação Gráfica: A parábola que representa a função y = ax² + bx + c toca o eixo x em apenas um ponto, que é o vértice da parábola. Esse ponto de tangência corresponde à raiz real dupla da equação.

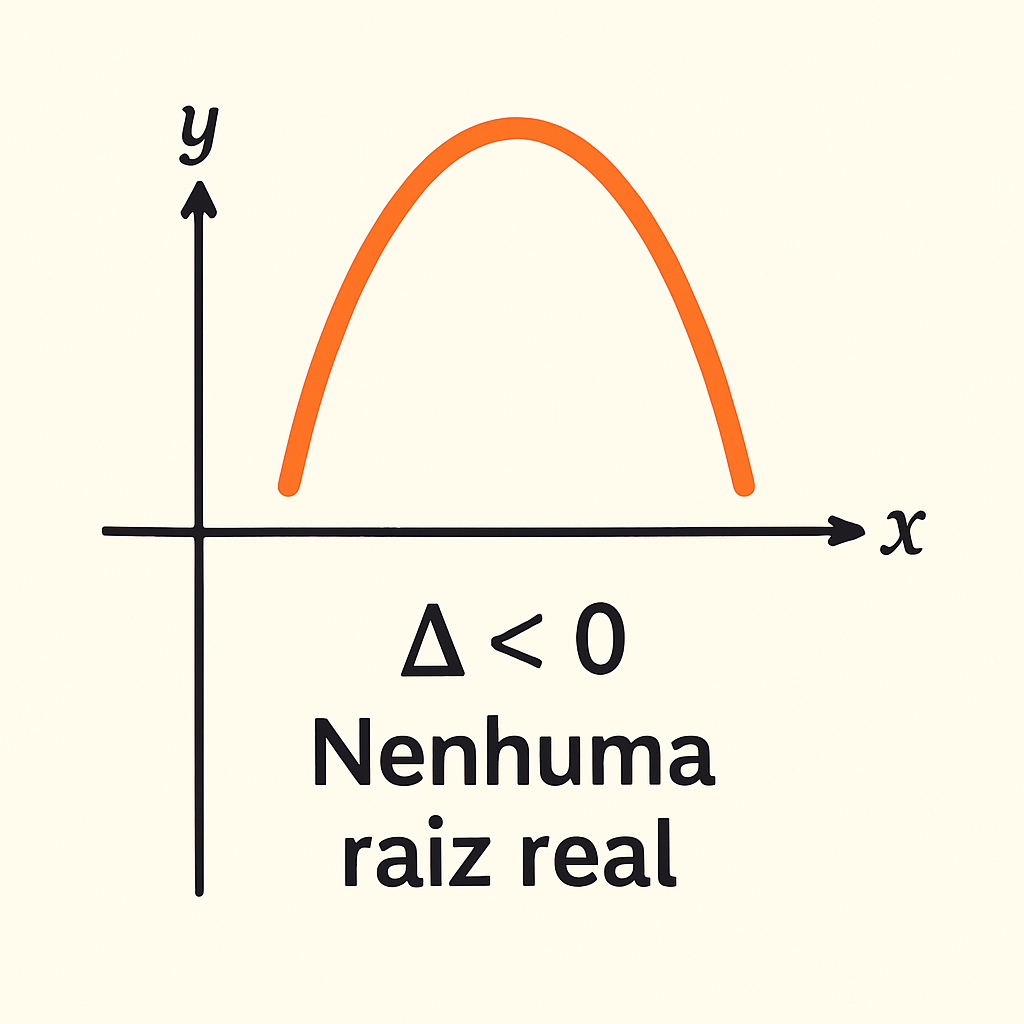
• Caso 3: Δ < 0 (Discriminante Negativo)

  • Significado Matemático: Quando Δ é negativo, não existe um número real que, elevado ao quadrado, resulte em Δ. Portanto, a raiz quadrada de Δ (√Δ) não é um número real. Como a fórmula de Bhaskara depende de √Δ, não podemos encontrar soluções dentro do conjunto dos números reais.

  • Conclusão: A equação não possui raízes reais.

  • Exemplo: Vimos que para x² + 2x + 5 = 0, Δ = -16 (negativo). Concluímos que não havia raízes reais.

  • Interpretação Gráfica: A parábola que representa a função y = ax² + bx + c não corta nem toca o eixo x. Ela fica inteiramente acima do eixo x (se a > 0) ou inteiramente abaixo do eixo x (se a < 0).

Por que analisar o Δ é importante?

1. Eficiência: Se você calcular Δ e ele for negativo, já sabe que não precisa continuar aplicando a fórmula de Bhaskara se estiver buscando apenas raízes reais. Você pode concluir imediatamente que não há solução real.

2. Compreensão: Ajuda a entender a natureza das soluções antes de encontrá-las.

3. Conexão Gráfica: Permite visualizar como a parábola associada à equação se comporta em relação ao eixo x.

A análise do discriminante é, portanto, um passo fundamental e esclarecedor no processo de resolução de equações do segundo grau.

6. Relações entre Coeficientes e Raízes: Os Segredos de Soma e Produto (Girard)

Além da Fórmula de Bhaskara, existe outra ferramenta muito útil para trabalhar com as raízes (x₁ e x₂) de uma equação do segundo grau ax² + bx + c = 0, especialmente quando o discriminante Δ é maior ou igual a zero (Δ ≥ 0). São as chamadas Relações de Girard, que estabelecem uma conexão direta entre os coeficientes (a, b, c) e a soma e o produto das raízes.

Essas relações são particularmente úteis para:

• Verificar se as raízes encontradas pela Fórmula de Bhaskara estão corretas.

• Encontrar as raízes de equações mais simples por tentativa e erro (quando as raízes são inteiras).

• Determinar uma equação do segundo grau conhecendo suas raízes.

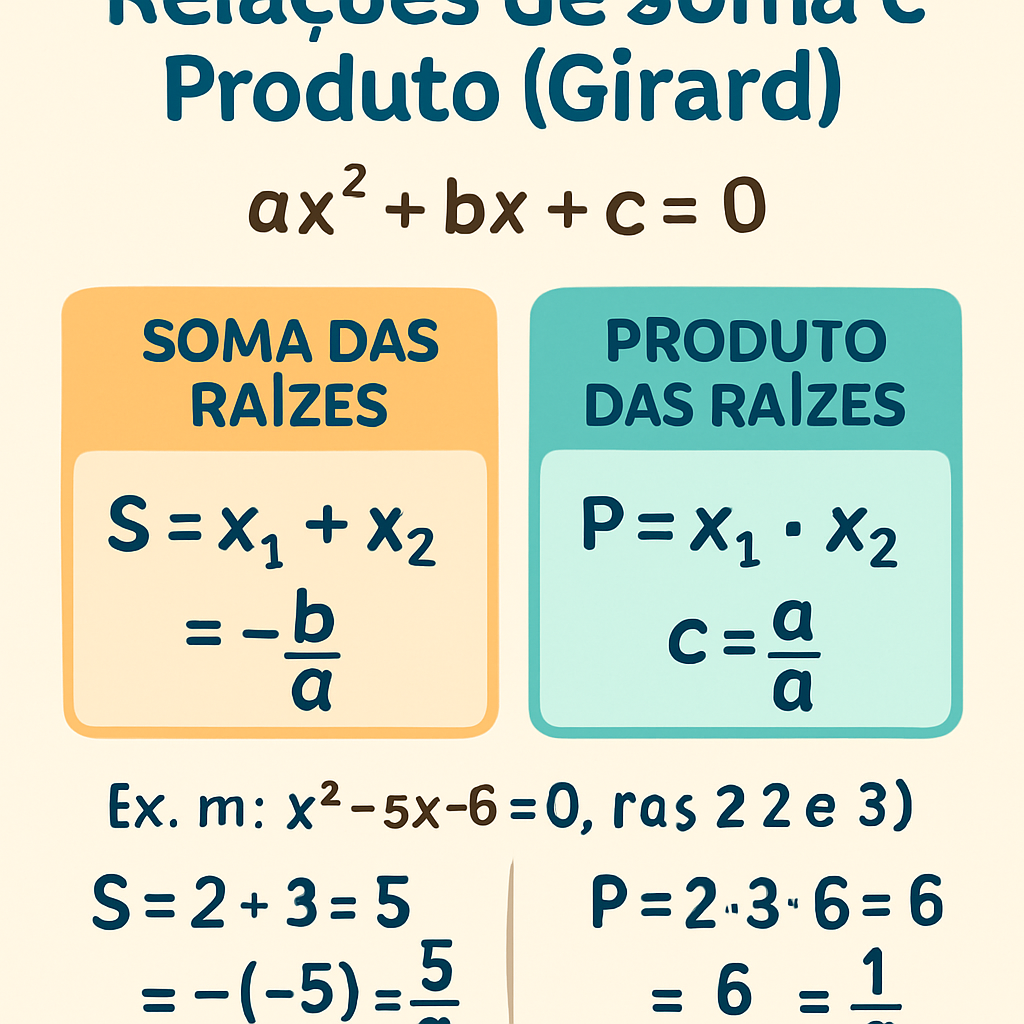
Soma das Raízes (S)

A soma das duas raízes (x₁ + x₂) de uma equação do segundo grau é dada pela relação:

S = x₁ + x₂ = -b / a

Ou seja, a soma das raízes é igual ao oposto do coeficiente b dividido pelo coeficiente a.

• Exemplo (Verificação): Para x² - 5x + 6 = 0, encontramos as raízes x₁ = 3 e x₂ = 2. Os coeficientes são a = 1, b = -5, c = 6.

  • Soma calculada pelas raízes: x₁ + x₂ = 3 + 2 = 5.

  • Soma calculada pela fórmula de Girard: S = -b / a = -(-5) / 1 = 5 / 1 = 5.

  • Como os resultados são iguais (5 = 5), isso reforça que nossas raízes estão corretas.

Produto das Raízes (P)

O produto das duas raízes (x₁ * x₂) de uma equação do segundo grau é dado pela relação:

P = x₁ * x₂ = c / a

Ou seja, o produto das raízes é igual ao coeficiente c dividido pelo coeficiente a.

• Exemplo (Verificação): Para x² - 5x + 6 = 0, com raízes x₁ = 3 e x₂ = 2, e coeficientes a = 1, b = -5, c = 6.

  • Produto calculado pelas raízes: x₁ x₂ = 3 2 = 6.

  • Produto calculado pela fórmula de Girard: P = c / a = 6 / 1 = 6.

  • Novamente, os resultados são iguais (6 = 6), confirmando as raízes.

Usando Soma e Produto para Encontrar Raízes (Método da Tentativa)

Para equações onde a = 1 (forma x² + bx + c = 0), as relações ficam mais simples: S = -b e P = c. Podemos tentar encontrar dois números que somados resultem em -b e multiplicados resultem em c.

• Exemplo: Resolver x² - 7x + 10 = 0

  • a = 1, b = -7, c = 10.

  • Procuramos dois números cuja soma seja S = -b = -(-7) = 7 e cujo produto seja P = c = 10.

  • Quais dois números multiplicados dão 10? (1 e 10, 2 e 5, -1 e -10, -2 e -5).

  • Desses pares, qual deles somado dá 7? O par 2 e 5 (2 + 5 = 7).

  • Portanto, as raízes são x₁ = 2 e x₂ = 5.

  • Este método é rápido quando as raízes são inteiras e fáceis de identificar.

Montando a Equação a partir das Raízes

Se conhecemos as raízes x₁ e x₂, podemos usar as relações de soma e produto para montar uma equação do segundo grau que tenha essas raízes. Uma forma comum é:

x² - Sx + P = 0

Onde S é a soma das raízes (x₁ + x₂) e P é o produto das raízes (x₁ * x₂).

• Exemplo: Encontrar uma equação do segundo grau cujas raízes são 4 e -1.

  • Soma (S) = 4 + (-1) = 3.

  • Produto (P) = 4 * (-1) = -4.

  • Substituindo na forma x² - Sx + P = 0: x² - (3)x + (-4) = 0 x² - 3x - 4 = 0.

  • Esta é uma equação do segundo grau cujas raízes são 4 e -1.

As Relações de Girard são, portanto, um complemento valioso à Fórmula de Bhaskara, oferecendo caminhos alternativos para verificar soluções e resolver certos tipos de problemas de forma mais intuitiva.

7. Representação Gráfica: A Dança da Parábola

As equações do segundo grau não vivem apenas no mundo abstrato dos números e fórmulas; elas têm uma representação visual muito elegante e informativa: a parábola.

Quando pensamos na equação do segundo grau não apenas como algo a ser resolvido (ax² + bx + c = 0), mas como uma função quadrática (y = ax² + bx + c), podemos desenhar seu gráfico no plano cartesiano. O resultado é sempre uma curva suave em forma de "U" ou "U" invertido, chamada parábola.

Entender as características da parábola nos ajuda a visualizar as soluções da equação e a interpretar o significado dos coeficientes e do discriminante.

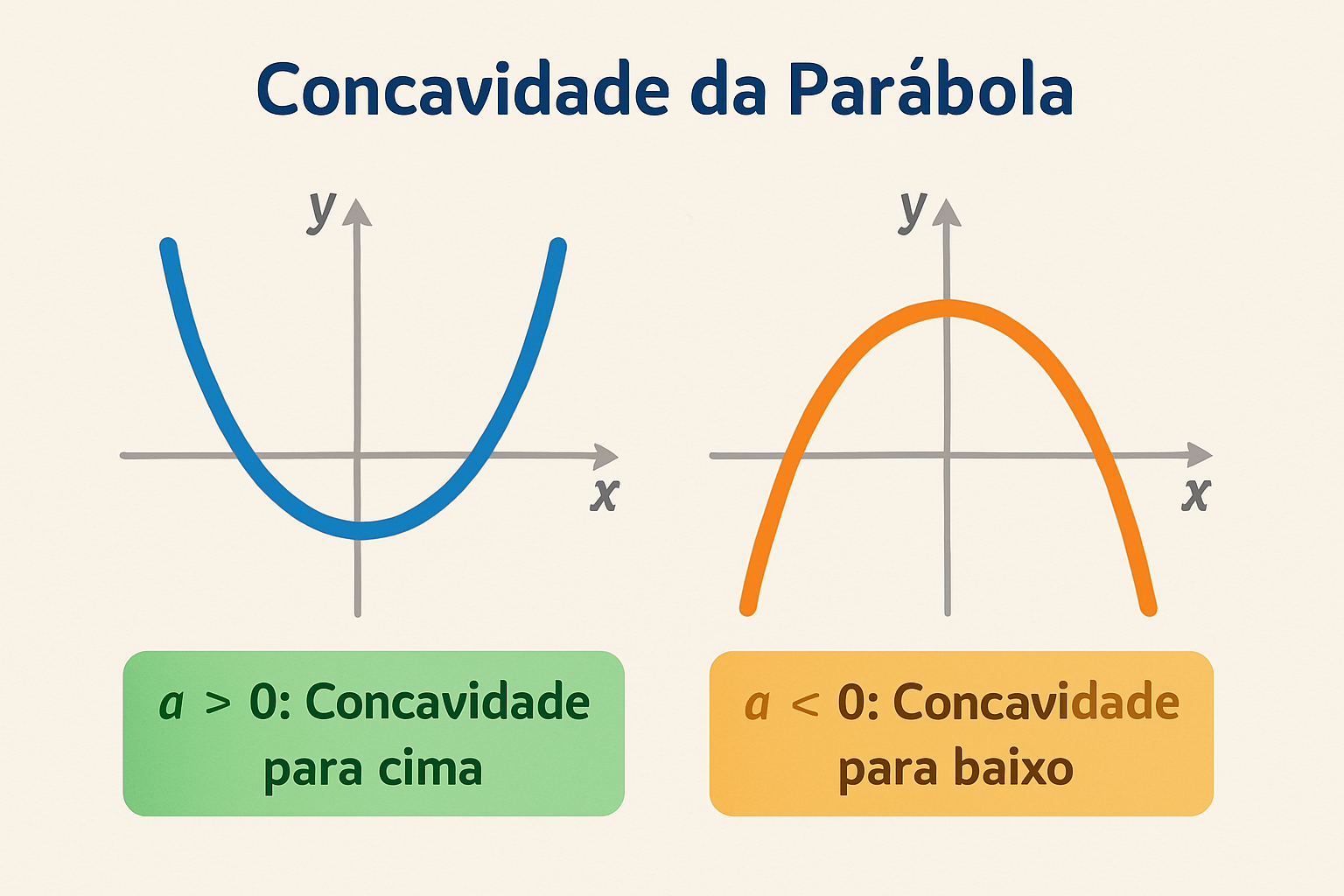
Concavidade: Para Cima ou Para Baixo?

A direção para onde a parábola se abre (sua concavidade) é determinada exclusivamente pelo sinal do coeficiente a:

• Se a > 0 (positivo): A parábola tem concavidade voltada para cima (parece uma "boca feliz" 😊).

• Se a < 0 (negativo): A parábola tem concavidade voltada para baixo (parece uma "boca triste" 😟).

O Vértice: O Ponto Chave da Parábola

Toda parábola possui um ponto muito especial chamado vértice (V). Ele representa:

• O ponto de mínimo da função (o ponto mais baixo da curva) se a > 0.

• O ponto de máximo da função (o ponto mais alto da curva) se a < 0.

As coordenadas do vértice (Xv, Yv) podem ser calculadas usando os coeficientes e o discriminante:

• Coordenada X do Vértice (Xv): Xv = -b / 2a

• Coordenada Y do Vértice (Yv): Yv = -Δ / 4a (onde Δ = b² - 4ac)

O vértice é importante porque ele define o eixo de simetria da parábola (uma linha vertical que passa por Xv e divide a parábola em duas metades espelhadas).

Raízes e Interseções com o Eixo X

As raízes reais da equação ax² + bx + c = 0 (os valores de x que encontramos usando Bhaskara) correspondem exatamente aos pontos onde a parábola intercepta o eixo x.

• Se Δ > 0, a equação tem duas raízes reais distintas, e a parábola corta o eixo x em dois pontos (x₁, 0) e (x₂, 0).

• Se Δ = 0, a equação tem uma raiz real dupla, e a parábola toca o eixo x em um único ponto, que é o vértice (Xv, 0).

• Se Δ < 0, a equação não tem raízes reais, e a parábola não corta nem toca o eixo x.

Interseção com o Eixo Y

A parábola sempre intercepta o eixo y em um ponto. Para encontrar esse ponto, basta fazer x = 0 na função y = ax² + bx + c:

y = a(0)² + b(0) + c y = c

Portanto, a parábola sempre corta o eixo y no ponto (0, c), onde c é o termo independente da equação.

Esboçando o Gráfico

Com essas informações (concavidade, vértice, raízes e interseção com o eixo y), podemos fazer um esboço bastante preciso do gráfico da parábola associada a uma equação do segundo grau.

• Exemplo: Esboçar o gráfico de y = x² - 4x + 3

  1. Coeficientes: a = 1, b = -4, c = 3.

  2. Concavidade: Como a = 1 (a > 0), a concavidade é para cima.

  3. Interseção com eixo y: Ocorre em (0, c) = (0, 3).

  4. Raízes (interseção com eixo x): Resolvemos x² - 4x + 3 = 0.

     • Δ = (-4)² - 4 1 3 = 16 - 12 = 4.

     • x = [-(-4) ± √4] / (2 * 1) = [4 ± 2] / 2.

     • x₁ = (4 + 2) / 2 = 3.

     • x₂ = (4 - 2) / 2 = 1.

     • A parábola corta o eixo x em (1, 0) e (3, 0).

  5. Vértice:

     • Xv = -b / 2a = -(-4) / (2 * 1) = 4 / 2 = 2.

     • Yv = -Δ / 4a = -4 / (4 * 1) = -1.

     • O vértice é V = (2, -1).

  6. Esboço: Marcamos os pontos (0, 3), (1, 0), (3, 0) e (2, -1) e desenhamos uma parábola suave com concavidade para cima passando por eles.

A representação gráfica nos dá uma compreensão visual profunda do comportamento das equações do segundo grau e do significado de suas raízes e coeficientes.

8. Aplicações Práticas: Onde a Equação do Segundo Grau Aparece no Mundo Real?

A equação do segundo grau não é apenas um exercício teórico da matemática; ela surge naturalmente na modelagem de diversos fenômenos do mundo real. Conhecer algumas dessas aplicações nos ajuda a entender a relevância e o poder dessa ferramenta matemática.

• Física - Lançamento de Projéteis: A trajetória de um objeto lançado obliquamente (como uma bola de basquete arremessada à cesta ou uma bala de canhão) descreve uma parábola. A altura do objeto em função do tempo ou da distância horizontal pode ser modelada por uma equação do segundo grau. Podemos usá-la para calcular a altura máxima atingida, o alcance do lançamento ou o tempo de voo.

  • [IMAGEM: Ilustração da trajetória parabólica de uma bola sendo lançada]

• Geometria - Problemas de Área: Muitas vezes, ao trabalharmos com áreas de figuras geométricas, especialmente quando buscamos otimizar (maximizar ou minimizar) uma área sob certas condições, recaímos em equações do segundo grau. Por exemplo, determinar as dimensões de um terreno retangular de área máxima que pode ser cercado com uma quantidade fixa de cerca.

• Engenharia e Arquitetura: O formato parabólico é encontrado em diversas estruturas devido às suas propriedades de distribuição de força e foco. Exemplos incluem:

  • Pontes suspensas: Os cabos principais frequentemente assumem a forma de uma parábola.

  • Antenas parabólicas e refletores: Utilizam a propriedade da parábola de refletir ondas (de rádio, luz, som) para um ponto focal.

  • Arcos e abóbadas: Estruturas arquitetônicas que podem ter seções parabólicas.

• Economia e Negócios: Em modelos econômicos simplificados, a relação entre o preço de um produto e a receita obtida, ou entre a quantidade produzida e o custo ou lucro, pode ser representada por uma função quadrática. A equação do segundo grau pode ser usada para encontrar o preço que maximiza a receita, a quantidade que minimiza o custo ou os pontos de equilíbrio (lucro zero).

• Problemas do Cotidiano: Situações aparentemente simples podem envolver equações do segundo grau. Por exemplo, se dois carros partem de um mesmo ponto em direções perpendiculares com velocidades constantes, a distância entre eles em função do tempo pode envolver uma relação quadrática (pelo Teorema de Pitágoras).

Exemplo Prático Resolvido:

Um fazendeiro quer construir um cercado retangular usando 100 metros de cerca. Quais devem ser as dimensões do cercado para que a área seja a maior possível?

1. Modelagem: Seja x o comprimento e y a largura do retângulo.

   • Perímetro: 2x + 2y = 100 => x + y = 50 => y = 50 - x.

   • Área: A = x y. Substituindo y, temos A(x) = x (50 - x) = 50x - x².

2. Equação/Função: A área é dada pela função quadrática A(x) = -x² + 50x. Queremos encontrar o valor de x que maximiza A(x).

3. Resolução: A função A(x) = -x² + 50x representa uma parábola com concavidade para baixo (a = -1 < 0). O valor máximo da área ocorre no vértice.

   • Xv = -b / 2a = -50 / (2 * -1) = -50 / -2 = 25.

   • Este é o valor do comprimento x que maximiza a área.

   • A largura correspondente é y = 50 - x = 50 - 25 = 25.

4. Resposta: Para obter a área máxima, o cercado deve ser um quadrado com lados de 25 metros.

Esses exemplos demonstram como a equação do segundo grau é uma ferramenta essencial para descrever e resolver problemas em diversas áreas.

9. Estratégias para Resolução de Problemas: Um Roteiro para o Sucesso

Resolver problemas que envolvem equações do segundo grau, especialmente aqueles que vêm de contextos práticos, requer mais do que apenas saber aplicar a fórmula de Bhaskara. É preciso interpretar o problema, traduzi-lo para a linguagem matemática e, finalmente, resolver a equação encontrada, sem esquecer de verificar se a solução faz sentido.

[IMAGEM: Fluxograma claro e simples para resolução de problemas com equação do 2º grau]

Aqui está um roteiro passo a passo que pode ajudar:

1. Leia com Atenção e Compreenda o Enunciado: Qual é a pergunta do problema? Quais informações são fornecidas? Quais são as grandezas envolvidas?

2. Identifique a(s) Incógnita(s): O que você precisa descobrir? Represente essa(s) quantidade(s) por uma variável (geralmente x).

3. Traduza para a Linguagem Matemática: Use as informações do enunciado para escrever uma ou mais equações que relacionem as incógnitas e os dados fornecidos. Procure por relações que levem a uma expressão quadrática.

4. Monte a Equação do Segundo Grau: Manipule a(s) equação(ões) encontradas até chegar à forma padrão ax² + bx + c = 0.

5. Resolva a Equação: Escolha o método mais apropriado:

   • Se for incompleta (b=0 ou c=0), use os métodos específicos (isolar x² ou fatorar).

   • Se for completa, use a Fórmula de Bhaskara (calculando Δ primeiro).

6. Encontre as Raízes: Calcule os possíveis valores para a incógnita x.

7. Analise as Soluções no Contexto do Problema: Este é um passo crucial! Verifique se as raízes encontradas fazem sentido na situação real descrita.

   • Medidas de comprimento, área, tempo, etc., geralmente não podem ser negativas. Se uma raiz for negativa, ela pode precisar ser descartada como solução válida para o problema (embora seja uma solução válida para a equação matemática).

   • Existem outras restrições impostas pelo problema?

8. Formule a Resposta: Escreva a resposta final de forma clara, respondendo à pergunta original do problema e incluindo as unidades corretas, se aplicável.

Dica: Fazer um desenho ou um esquema da situação descrita no problema pode ajudar muito na interpretação e na montagem da equação.

Seguir essas estratégias de forma organizada aumenta significativamente as chances de resolver corretamente problemas que envolvem equações do segundo grau.

10. Conclusão: Dominando a Equação do Segundo Grau

Chegamos ao final da nossa exploração sobre a equação do segundo grau! Percorremos um longo caminho, desde a compreensão de sua forma geral ax² + bx + c = 0 e a identificação de seus coeficientes, passando pelos diferentes tipos (completas e incompletas) e seus métodos específicos de resolução.

Aprofundamo-nos na poderosa Fórmula de Bhaskara, desvendando o papel crucial do discriminante Δ em determinar a natureza e a quantidade de raízes reais. Vimos também como as Relações de Girard (soma e produto) nos oferecem atalhos para verificar resultados e até mesmo encontrar raízes em casos mais simples.

Além disso, conectamos a álgebra com a geometria ao visualizar a equação do segundo grau como uma função quadrática, cujo gráfico é sempre uma parábola. Analisamos como a concavidade, o vértice e as interseções com os eixos estão diretamente ligados aos coeficientes e às raízes da equação.

Finalmente, vimos como esse conceito matemático fundamental se aplica a problemas práticos em diversas áreas, da física à economia, e estabelecemos estratégias claras para modelar e resolver esses problemas.

Dominar a equação do segundo grau abre portas para uma compreensão mais profunda da matemática e do mundo ao nosso redor. Embora possa parecer complexa no início, a chave está na prática consistente. Resolva os exercícios propostos, revise os exemplos e não hesite em buscar ajuda quando encontrar dificuldades.

Esperamos que este guia tenha sido um recurso valioso em sua jornada de aprendizado. Continue praticando, explorando e descobrindo a beleza e a utilidade da matemática!

Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=r-Vuvb18kUk

Canal: Dicasdemat Sandro Curió

http://www.youtube.com/watch?v=LNLvMo1PWok

Canal: Gis com Giz Matemática