Equação do 1° grau
Equação do Primeiro Grau: Guia Completo e Didático
A equação do primeiro grau é um dos conceitos fundamentais da matemática que todo estudante precisa dominar. Uma equação linear é uma expressão algébrica que possui uma incógnita (geralmente representada pela letra x) elevada à primeira potência, ou seja, sem expoentes maiores que 1. Compreender a equação linear é essencial para o desenvolvimento do raciocínio lógico-matemático e serve como base para conceitos mais avançados da álgebra.
O que é uma Equação do Primeiro Grau?
Uma equação linear, também conhecida como equação do primeiro grau, é uma igualdade matemática que contém uma ou mais incógnitas elevadas à primeira potência. Uma equação do primeiro grau com uma variável pode ser representada pela seguinte fórmula geral:
ax + b = 0
Onde:
•x é a incógnita (variável)
•a ≠ 0 (condição obrigatória)
A condição a ≠ 0 é fundamental, pois se a = 0, a expressão deixaria de ser uma Equação do 1° Grau e se tornaria uma equação de grau zero ou uma identidade.
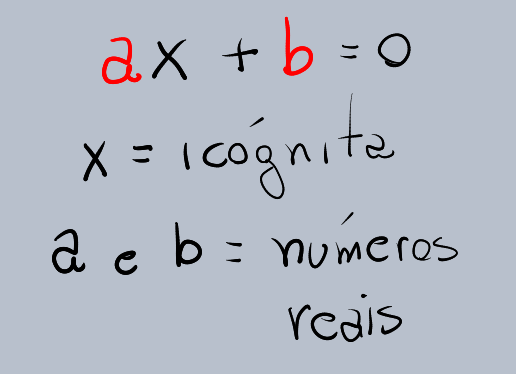
Características Principais
1. Grau da Equação: O x tem, no máximo, expoente 1
Número de soluções: Uma equação linear sempre possui uma única solução real
Representação gráfica: o gráfico de uma equação do primeiro grau é sempre uma reta
Linearidade: A relação entre as variáveis é linear, sem termos quadráticos ou de graus superiores
Elementos Fundamentais da Equação do Primeiro Grau
Para compreender completamente uma equação do primeiro grau, é necessário conhecer seus elementos constituintes:
Coeficientes
Na equação linear ax + b = 0:
a é chamado de coeficiente angular ou coeficiente da incógnita
O termo ‘b’ são números reais, também chamado de coef/ linear
Incógnita
A incógnita representa a variável cujo valor estamos tentando encontrar. Embora tradicionalmente seja representada pela letra x, pode ser qualquer letra do alfabeto (y, z, t, etc.).
Igualdade
O sinal de igual (=) estabelece os dois membros de uma equação:
Primeiro membro: parte à esquerda do sinal de igualdade
Segundo Membro: parte à direita do sinal de igualdade
Como Resolver uma Equação do Primeiro Grau
A solução de uma equação de primeiro grau é o valor específico da variável que satisfaz a igualdade proposta. Para fazer isso, utilizamos um processo baseado nas regras fundamentais da álgebra.
Princípios Básicos para Resolução
1. Princípio Aditivo: Permite somar ou subtrair o mesmo valor de ambos os membros.
2. Princípio Multiplicativo: Esta regra afirma que a igualdade de uma equação se mantém se multiplicarmos ou dividirmos ambos os seus membros por um mesmo número exceto o 0.
Princípio da Transposição: Podemos “passar” um termo de um membro para outro, invertendo sua operação
Método Passo a Passo
Para resolver uma equação do primeiro grau, seguimos estes passos:
Passo 1: Eliminar parênteses e simplificar expressões Passo 2: Agrupar termos semelhantes Passo 3: Isolar os termos com incógnita em um membro Passo 4: Isolar os termos independentes no outro membro Passo 5: Dividir ambos os membros pelo coeficiente da incógnita
Exemplo Prático de Resolução
Vamos seguir o passo a passo para resolver a equação: 3x + 7 = 22.
Passo 1: A equação já está simplificada
Passo 2: Não há termos semelhantes para agrupar
Passo 3: Subtraímos 7 de ambos os membros 3x + 7 – 7 = 22 – 7 3x = 15
Passo 4: Dividimos ambos os membros por 3 3x ÷ 3 = 15 ÷ 3 x = 5
Verificação: Substituindo x = 5 na equação original: 3(5) + 7 = 15 + 7 = 22 ✓
Método: Passar para o Outro Lado com o Sinal Invertido
Com este método podemos simplificar a maneira que este cálculo funciona e ajuda no entendimento. Á ideia é que efetuar a operação em ambos os lados da equação resulta no mesmo que passar o número para o outro lado com seu sinal invertido, Veja o passo a passo da técnica:
Exemplo 1:
Passo 1: Identificar o Termo a Ser Movido
A equação dada é:
x + 13 = 40
Queremos isolar x. O termo que está junto com x e que precisamos mover é o + 13.
Passo 2: Mover o Termo e Inverter o Sinal
Quando movemos o + 13 para o segundo membro da equação, devemos inverter a sua operação, de adição para subtração. Assim, o + 13 se torna – 13 no segundo membro
x = 40 – 13
Passo 3: Realizar a Operação
Agora, efetuamos a conta no segundo membro da equação:
40 – 13 = 27
Passo 4: Apresentar o Resultado
Após estes passos a resposta aparece
x = 27
Exemplo 2:
Passo 1: Identificar o Termo a Ser Movido
A equação dada é:
4x = 48
Queremos isolar x. O termo que está junto com x e que precisamos mover é o 4. Note que 4x significa 4 * x (4 multiplicado por x).
Passo 2: Mover o Termo e Inverter o Sinal
Quando movemos o 4 do lado esquerdo para o lado direito da equação, sua operação (multiplicação) é invertida para divisão. Assim, o 4 que estava multiplicando x passa a dividir o 48 no lado direito.
x = 48 / 4
Passo 3: Realizar a Operação
Agora, realizamos a divisão no segundo membro:
48 / 4 = 12
Passo 4: Apresentar o Resultado
Agora, apenas veja o resultado:
x = 12
Exemplo 3
Passo 1: Mover os Termos com ‘x’ para um Lado
A equação dada é:
2x + 15 = x + 25
Vamos mover o termo x do lado direito para o lado esquerdo. Como ele está positivo (+x) no lado direito, ele passará para o lado esquerdo com o sinal invertido, ou seja, negativo (-x).
2x – x + 15 = 25
Passo 2: Mover os Termos Constantes para o Outro Lado
Agora, vamos mover o termo constante +15 do lado esquerdo para o lado direito. Como ele está positivo (+15) no lado esquerdo, ele passará para o lado direito com o sinal invertido, ou seja, negativo (-15).
2x – x = 25 – 15
Passo 3: Realizar as Operações
Agora, realizamos as operações em ambos os lados da equação:
No lado esquerdo (termos com x): 2x – x = x
No lado direito (termos constantes): 25 – 15 = 10
Passo 4: Apresentar o Resultado
Após realizar as operações, a equação se simplifica para:
x = 10
Tipos Especiais de Equação do 1° Grau
Existem diferentes apresentações das equações lineares que requerem técnicas específicas de resolução:
Equações com Frações
Quando uma equação do primeiro grau contém frações, devemos encontrar o mínimo múltiplo comum (MMC) dos denominadores e multiplicar toda a equação por esse valor.
Exemplo: x/2 + x/3 = 10
A estratégia para se livrar dos números de baixo da fração é usar o MMC. Calculando o MMC de 2 e 3, encontramos o valor 6. Depois, multiplica a conta toda por 6.Com isso, a equação é transformada em 3x + 2x = 60. Juntando os ‘x’, temos 5x = 60. Fazendo a conta de 60 dividido por 5, a gente descobre que o x vale 12.
Equações com Parênteses
Para resolver uma equação do primeiro grau com parênteses, aplicamos a propriedade distributiva antes de prosseguir com a resolução.
Resolvendo a equação com parênteses: 2(x + 3) = 4x – 2.
Aplicando a distributiva: 2x + 6 = 4x – 2
Isolando x: 2x – 4x = -2 – 6 -2x
= -8 x = 4
Aplicações Práticas da Equação do 1° Grau
Este tipo de equação não é apenas um conceito teórico; ela tem inúmeras aplicações práticas no cotidiano:
Problemas de Idade
Problemas que pedem para descobrir a idade de alguém frequentemente podem ser modelados e resolvidos usando uma equação de primeiro grau.
Exemplo: João tem 5 anos a mais que Maria. A soma das idades é 35 anos. Qual a idade de cada um?
Para resolver o problema, primeiro definimos a idade de Maria como ‘x’. Como João é 5 anos mais velho, sua idade é ‘x + 5’. O problema diz que a soma das idades é 35, então montamos a equação: x + (x + 5) = 35. Simplificando, somamos os ‘x’ para obter 2x + 5 = 35. Em seguida, subtraímos 5 de ambos os lados, o que nos dá 2x = 30. Finalmente, dividindo por 2, descobrimos que a idade de Maria (x) é 15 anos.
Maria tem 15 anos e João tem 20 anos.
Problemas Financeiros
Problemas do dia a dia sobre preços, descontos e lucros são frequentemente modelados e solucionados por meio de equações lineares
Exemplo: Um produto custava R$80,00 e sofreu um desconto de R$68,00. Qual foi a porcentagem de desconto?
Seja x a porcentagem de desconto: 80 – (80 × x/100) = 68 80 – 0,8x = 68 -0,8x = -12 x = 15
O desconto foi de 15%.
Problemas de Movimento
Questões envolvendo velocidade, tempo e distância também utilizam equações do primeiro grau.
Exemplo: Um carro percorre uma distância em 3 horas a 60 km/h. Quanto tempo levaria para percorrer a mesma distância a 90 km/h?
Primeiro, a gente descobre a distância da viagem: 60 km/h por 3 horas dá 180 km. Agora, para saber o tempo (‘t’) que levaria a 90 km/h, a gente monta a conta: 90 vezes ‘t’ tem que dar 180. Dividindo 180 por 90, a gente acha que o tempo é de 2 horas
Sistemas de Equação do 1° Grau
Quando temos duas ou mais equações do 1° grau com duas ou mais incógnitas, formamos um sistema de equações. A resolução de sistemas é uma extensão natural do estudo das equações lineares.
Métodos de Resolução de Sistemas
Método da Substituição
Método da Adição/Eliminação
Método Gráfico
Exemplo de Sistema
x + y = 10 2x – y = 5
Somando as equações: 3x = 15 x = 5
Substituindo: 5 + y = 10, logo y = 5
Erros Comuns na Resolução de Exercícios
Estudantes frequentemente cometem erros específicos ao resolver uma equação do primeiro grau:
Erro de Sinal
Um dos erros mais comuns é trocar o sinal ao transpor termos de um membro para outro.
Incorreto: x + 3 = 7 → x = 7 + 3 Correto: x + 3 = 7 → x = 7 – 3
Erro na Propriedade Distributiva
Outro erro frequente ocorre ao aplicar a propriedade distributiva.
Incorreto: 2(x + 3) = 2x + 3 Correto: 2(x + 3) = 2x + 6
Erro na Verificação
Muitos estudantes esquecem de verificar se a solução encontrada realmente satisfaz a equação linear original.
Dicas para Dominar a Equação do 1° Grau
Para se tornar proficiente na resolução de equações do primeiro grau, considere estas estratégias:
Prática Constante
A resolução de equações lineares requer prática regular. Resolva diferentes tipos de problemas diariamente.
Verificação Sistemática
Sempre verifique sua resposta substituindo o valor encontrado na equação original.
Organização
Mantenha seus cálculos organizados, escrevendo cada passo claramente.
Compreensão Conceitual
Não apenas memorize os procedimentos; compreenda o porquê de cada passo na resolução de uma equação do primeiro grau.
Conexões com Outros Tópicos Matemáticos
As equações do primeiro grau servem como base para diversos outros conceitos matemáticos:
Funções Lineares
As equações lineares estão diretamente relacionadas às funções lineares, sendo sua representação algébrica.
Inequações
As inequações do 1° grau seguem princípios similares aos da Equação do 1° Grau, com algumas adaptações.
Geometria Analítica
Na geometria analítica, a equação do primeiro grau representa retas no plano cartesiano.
Progressões Aritméticas
As progressões aritméticas podem ser modeladas através de uma equação linear.
Importância da Equação do 1° Grau na Educação Matemática
O estudo das equações do primeiro grau é fundamental no currículo matemático por várias razões:
Desenvolvimento do Pensamento Algébrico
As equações lineares introduzem conceitos algébricos essenciais como variáveis, coeficientes e manipulação simbólica.
Preparação para Tópicos Avançados
Dominar a equação do primeiro grau é prerequisito para estudar equações de graus superiores, sistemas lineares e cálculo.
Aplicação Prática
As equações do primeiro grau modelam inúmeras situações do mundo real, desenvolvendo habilidades de resolução de problemas.
Raciocínio Lógico
A resolução sistemática de uma equação linear desenvolve o raciocínio lógico e sequencial.
Tecnologia e Equação do 1° Grau
Atualmente, diversas ferramentas tecnológicas auxiliam no ensino e aprendizagem das equações do primeiro grau:
Calculadoras Gráficas
Permitem visualizar graficamente as equações lineares e suas propriedades.
Software Matemático
Programas como GeoGebra facilitam a exploração interativa das equações do primeiro grau.
Aplicativos Educacionais
Diversos aplicativos oferecem exercícios interativos sobre equações do primeiro grau.
Plataformas Online
Sites educacionais proporcionam recursos multimídia para o estudo das equações do primeiro grau.
Desafios Comuns e Como Superá-los ao Estudar Equação do 1° Grau
Embora a equação do primeiro grau seja um conceito fundamental, muitos estudantes enfrentam desafios em sua compreensão e resolução. Identificar esses desafios e aplicar estratégias eficazes pode transformar a experiência de aprendizado.
Dificuldade com a Transposição de Termos
Um dos maiores obstáculos é a correta transposição de termos. Muitos se confundem com a mudança de sinal ao mover um termo de um lado para o outro de uma equação linear. A chave é lembrar que a operação inversa deve ser aplicada. Se um termo está somando de um lado, ele subtrai do outro; se está multiplicando, divide, e assim por diante. Praticar com exemplos variados e visualizar a equação como uma balança pode ajudar a solidificar esse conceito.
Erros na Aplicação da Propriedade Distributiva
Quando a equação do primeiro grau envolve parênteses, a propriedade distributiva é essencial. Erros comuns incluem multiplicar apenas o primeiro termo dentro do parêntese ou esquecer de aplicar o sinal negativo que precede o parêntese a todos os termos internos. A solução é ser meticuloso, aplicando a distributiva a cada termo e prestando atenção aos sinais.
Confusão com Frações e Denominadores
Equações do primeiro grau com frações podem parecer intimidantes. O erro mais comum é não encontrar o MMC corretamente ou não multiplicar todos os termos da equação por ele. Lembre-se que o objetivo é eliminar os denominadores para simplificar a equação linear. Praticar a simplificação de frações e o cálculo do MMC é crucial.
Conclusão
A equação do primeiro grau é um pilar fundamental da matemática que todo estudante deve dominar completamente. Sua compreensão vai além da simples memorização de procedimentos; envolve o desenvolvimento do pensamento algébrico, raciocínio lógico e habilidades de resolução de problemas. Através da prática constante e compreensão conceitual, os estudantes podem não apenas resolver qualquer equação linear, mas também aplicar esse conhecimento em situações práticas do cotidiano. O domínio das equações do primeiro grau abre portas para conceitos matemáticos mais avançados e contribui significativamente para a formação de um pensamento matemático sólido e estruturado.
Algumas video-aulas sobre o assunto:
http://www.youtube.com/watch?v=x4k8950MVeg
Canal: Dicasdemat Sandro Curió
http://www.youtube.com/watch?v=j6dy4VrsFvA
Canal: Gis com Giz Matemática
