Divisão de inteiros
Anderson Luiz Floriano Dos Santos
6/14/202518 min read
Divisão de Números Inteiros: O Guia Completo para Dominar a Operação Essencial da Matemática
A divisão é uma das quatro operações fundamentais da aritmética, ao lado da adição, subtração e multiplicação. Ela desempenha um papel crucial não apenas no universo da matemática, mas também em inúmeras situações do nosso cotidiano. Desde a simples tarefa de repartir um bolo entre amigos até cálculos complexos em engenharia ou finanças, a divisão se faz presente, permitindo-nos distribuir quantidades, agrupar elementos e compreender relações proporcionais. No entanto, para muitos, a divisão pode parecer uma operação desafiadora, repleta de regras e algoritmos que, à primeira vista, podem confundir.
Historicamente, a necessidade de dividir surgiu com as primeiras civilizações, que precisavam repartir terras, alimentos e outros recursos de forma justa. Métodos rudimentares de divisão foram desenvolvidos por egípcios, babilônios e gregos, evoluindo ao longo dos séculos até chegarmos aos algoritmos que utilizamos hoje. A compreensão da divisão é um pilar para o avanço em conceitos matemáticos mais complexos, como frações, decimais, porcentagens e álgebra. Dominá-la não é apenas uma questão de memorizar procedimentos, mas de entender a lógica por trás da operação e suas diversas aplicações.
Este guia completo tem como objetivo desmistificar a divisão de números inteiros, tornando-a acessível e compreensível para todos. Abordaremos desde os conceitos fundamentais e as diferentes formas de interpretar essa operação, até o passo a passo detalhado do algoritmo da divisão, conhecido como divisão longa. Além disso, exploraremos a importância do resto, as aplicações práticas da divisão no dia a dia e ofereceremos dicas valiosas para você aprimorar suas habilidades. Prepare-se para mergulhar no fascinante mundo da divisão e descobrir como essa operação pode ser simples e intuitiva quando bem compreendida.
Conceitos Fundamentais da Divisão
Para compreender a divisão em sua totalidade, é essencial familiarizar-se com os termos e conceitos que a compõem. Assim como em outras operações, a divisão possui elementos específicos que desempenham papéis distintos e são cruciais para a sua correta execução e interpretação.
Dividendo, Divisor, Quociente e Resto
Vamos imaginar a operação de divisão como a ação de distribuir uma quantidade total em grupos menores. Cada um desses termos representa uma parte fundamental desse processo:
•Dividendo (D): É o número que será dividido, ou seja, a quantidade total que será repartida. É o valor inicial da operação. Por exemplo, na expressão 20 ÷ 5, o 20 é o dividendo.
•Divisor (d): É o número pelo qual o dividendo será dividido. Ele indica em quantas partes o dividendo será repartido ou o tamanho de cada grupo. Na expressão 20 ÷ 5, o 5 é o divisor.
•Quociente (Q): É o resultado da divisão. Ele representa quantas vezes o divisor cabe no dividendo, ou a quantidade em cada parte, ou o número de grupos formados. Na expressão 20 ÷ 5, o quociente é 4.
•Resto (R): É a quantidade que sobra após a divisão, quando o dividendo não é um múltiplo exato do divisor. O resto é sempre um número menor que o divisor. Se o resto for zero, a divisão é exata. Por exemplo, na divisão 22 ÷ 5, o quociente é 4 e o resto é 2.
Exemplo: Se temos 20 maçãs para dividir igualmente entre 5 crianças:
•Dividendo: 20 (o total de maçãs)
•Divisor: 5 (o número de crianças)
•Quociente: 4 (cada criança receberá 4 maçãs)
•Resto: 0 (não sobrou nenhuma maçã)
Divisão Exata vs. Divisão Não Exata
A natureza do resto define se uma divisão é exata ou não exata:
•Divisão Exata: Ocorre quando o resto da divisão é zero. Isso significa que o dividendo é um múltiplo do divisor, e a divisão pode ser feita sem sobras. Ex: 15 ÷ 3 = 5 (resto 0).
•Divisão Não Exata (ou Divisão com Resto): Ocorre quando o resto da divisão é um número diferente de zero. Isso indica que o dividendo não é um múltiplo exato do divisor, e há uma sobra após a distribuição. Ex: 17 ÷ 3 = 5 (resto 2).
Propriedades da Divisão
Ao contrário da adição e da multiplicação, a divisão possui algumas particularidades importantes em relação às suas propriedades:
•Não Comutativa: A ordem dos números na divisão altera o resultado. Ou seja, a ÷ b é diferente de b ÷ a (a menos que a = b). Ex: 10 ÷ 2 = 5, mas 2 ÷ 10 = 0,2 (que não é um número inteiro, mas ilustra a diferença).
•Não Associativa: A forma como agrupamos os números em uma sequência de divisões afeta o resultado. Ou seja, (a ÷ b) ÷ c é diferente de a ÷ (b ÷ c). Ex: (24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3, mas 24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12.
•Elemento Neutro (Divisão por 1): Qualquer número inteiro dividido por 1 resulta no próprio número. O número 1 é o elemento neutro da divisão. Ex: 7 ÷ 1 = 7.
•Divisão por Zero: A divisão por zero é uma operação indefinida na matemática. Não é possível dividir um número por zero. Tentar fazê-lo leva a uma indeterminação ou a um resultado impossível de ser definido. É uma regra fundamental a ser lembrada: o divisor nunca pode ser zero.
Relação com a Multiplicação: A Operação Inversa
A divisão e a multiplicação são operações inversas. Isso significa que uma
desfaz a outra. Se você multiplicar um número e depois dividi-lo pelo mesmo fator, você retorna ao número original. Essa relação é fundamental para verificar os resultados da divisão e para entender a lógica por trás de muitos problemas matemáticos.
Por exemplo, se sabemos que 3 × 5 = 15, então podemos inferir que 15 ÷ 5 = 3 e 15 ÷ 3 = 5. Essa interconexão é uma ferramenta poderosa para a resolução de problemas e para a compreensão da estrutura dos números.
As Diferentes Interpretações da Divisão
A divisão, embora seja uma única operação matemática, pode ser compreendida e aplicada de diversas maneiras, dependendo do contexto do problema. Entender essas diferentes interpretações é crucial para aplicar a divisão corretamente em situações variadas e para desenvolver uma compreensão mais profunda de seu significado. Vamos explorar as principais formas de interpretar a divisão de números inteiros.
Divisão como Repartição Equitativa (Partição)
Esta é talvez a interpretação mais intuitiva da divisão. Nela, a divisão é vista como o ato de distribuir uma quantidade total (o dividendo) em um número específico de partes iguais (o divisor). O resultado (o quociente) indica a quantidade em cada uma dessas partes.
Exemplo: Imagine que você tem 12 biscoitos e quer dividi-los igualmente entre 3 amigos. Aqui, o dividendo é 12 (o total de biscoitos) e o divisor é 3 (o número de amigos). Ao realizar a divisão (12 ÷ 3 = 4), o quociente 4 nos diz que cada amigo receberá 4 biscoitos. Não há sobras, então o resto é 0.
Essa interpretação é comumente utilizada em situações do dia a dia que envolvem a distribuição justa de itens, como dividir uma conta de restaurante, repartir doces em uma festa ou distribuir tarefas entre membros de uma equipe. A chave aqui é que o número de grupos é conhecido, e buscamos a quantidade em cada grupo.
Divisão como Medida (Quotição)
Na interpretação da divisão como medida, estamos interessados em descobrir quantos grupos de um determinado tamanho (o divisor) podem ser formados a partir de uma quantidade total (o dividendo). O quociente, neste caso, representa o número de grupos que podem ser formados.
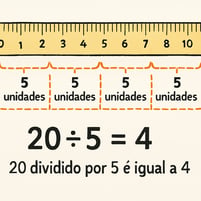
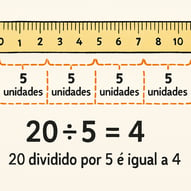
Exemplo: Suponha que você tenha 20 metros de fita e precise cortar pedaços de 5 metros cada para fazer laços. Aqui, o dividendo é 20 (o total de fita) e o divisor é 5 (o tamanho de cada pedaço). A divisão (20 ÷ 5 = 4) nos informa que você pode fazer 4 laços. Novamente, o resto é 0.
Essa interpretação é útil em cenários onde precisamos agrupar itens em conjuntos de um tamanho específico, como determinar quantas caixas são necessárias para embalar um certo número de produtos, quantos pacotes de figurinhas podem ser comprados com uma quantia de dinheiro, ou quantas viagens um caminhão precisa fazer para transportar uma carga total. A chave aqui é que o tamanho de cada grupo é conhecido, e buscamos o número de grupos.
Divisão como Operação Inversa da Multiplicação
Como já mencionado, a divisão é a operação inversa da multiplicação. Essa interpretação é fundamental para entender a relação entre as duas operações e para resolver equações. Se sabemos que a multiplicação de dois números resulta em um terceiro, a divisão nos permite encontrar um dos fatores se conhecermos o produto e o outro fator.
Exemplo: Se você sabe que um número multiplicado por 3 resulta em 15 (ou seja, ? × 3 = 15), a divisão nos permite encontrar esse número desconhecido. Ao dividir 15 por 3 (15 ÷ 3 = 5), descobrimos que o número é 5. Essa relação é a base para a verificação de resultados da divisão: se Q é o quociente de D ÷ d, então Q × d deve ser igual a D (considerando o resto, se houver).
Essa perspectiva é particularmente útil na álgebra e na resolução de problemas onde um valor desconhecido precisa ser determinado a partir de uma relação multiplicativa.
Divisão como Subtrações Sucessivas
Embora não seja o método mais eficiente para realizar divisões grandes, a interpretação da divisão como subtrações sucessivas oferece uma compreensão conceitual profunda do que a divisão realmente significa. Basicamente, consiste em subtrair o divisor do dividendo repetidamente até que o resultado seja menor que o divisor. O número de vezes que a subtração foi realizada é o quociente, e o valor final que resta é o resto.
Exemplo: Vamos dividir 10 por 3 usando subtrações sucessivas:
1.10 - 3 = 7 (1ª subtração)
2.7 - 3 = 4 (2ª subtração)
3.4 - 3 = 1 (3ª subtração)
Neste ponto, o resultado (1) é menor que o divisor (3). Contamos quantas vezes subtraímos o 3: foram 3 vezes. Portanto, o quociente é 3 e o resto é 1.
Essa abordagem visualiza a divisão como a remoção de grupos do tamanho do divisor do dividendo total. É uma excelente maneira de solidificar a compreensão do conceito de
divisão, especialmente para iniciantes, pois conecta a divisão diretamente à subtração, uma operação mais básica e familiar.
Compreender essas diferentes interpretações da divisão enriquece sua capacidade de resolver problemas e aplicar a matemática em diversas situações. A escolha da interpretação mais adequada depende do contexto do problema e do que se busca descobrir.
O Algoritmo da Divisão (Divisão Longa)
O algoritmo da divisão, frequentemente chamado de
divisão longa, é o método padrão para dividir números inteiros, especialmente quando o dividendo é grande. Embora possa parecer complexo à primeira vista, ele é um processo sistemático que, uma vez compreendido, permite resolver qualquer problema de divisão. Este algoritmo organiza a operação em uma série de passos repetitivos de divisão, multiplicação e subtração.
Passo a Passo Detalhado: Como Realizar a Divisão Longa
Vamos detalhar o processo da divisão longa utilizando um exemplo prático. Suponha que queremos dividir 735 por 5 (735 ÷ 5).
1.Montagem da Operação: Primeiro, organizamos os números no formato da divisão longa. O dividendo (735) fica dentro da
chave (ou 'casinha') e o divisor (5) fora dela.
2.Determinação do Primeiro Quociente: Começamos pelo algarismo mais à esquerda do dividendo (7). Perguntamos: "Quantas vezes o 5 cabe no 7?" O 5 cabe uma vez no 7. Escrevemos o 1 no quociente, abaixo da chave, alinhado com o 7.
3.Multiplicação e Subtração: Multiplicamos o algarismo que acabamos de colocar no quociente (1) pelo divisor (5): 1 × 5 = 5. Escrevemos o resultado (5) abaixo do 7 no dividendo e subtraímos.
4.Descida do Próximo Algarismo: Abaixamos o próximo algarismo do dividendo (o 3) ao lado do resultado da subtração (2), formando o número 23.
5.Repetição do Processo: Agora, repetimos os passos 2, 3 e 4 com o novo número (23). Perguntamos: "Quantas vezes o 5 cabe no 23?" O 5 cabe 4 vezes no 23 (pois 5 × 4 = 20). Escrevemos o 4 ao lado do 1 no quociente.
Multiplicamos o 4 pelo 5: 4 × 5 = 20. Escrevemos o 20 abaixo do 23 e subtraímos.
Abaixamos o próximo algarismo do dividendo (o 5) ao lado do resultado da subtração (3), formando o número 35.
Repetimos o processo com o 35. Perguntamos: "Quantas vezes o 5 cabe no 35?" O 5 cabe 7 vezes no 35 (pois 5 × 7 = 35). Escrevemos o 7 ao lado do 4 no quociente.
Multiplicamos o 7 pelo 5: 7 × 5 = 35. Escrevemos o 35 abaixo do 35 e subtraímos. O resultado é 0. Como não há mais algarismos para baixar, a divisão está completa. Portanto, 735 ÷ 5 = 147, com resto 0.
Exemplos Práticos
Vamos ver mais alguns exemplos para solidificar o entendimento do algoritmo da divisão.
Exemplo 1: Divisão Exata
Dividir 864 por 4.
Resultado: 864 ÷ 4 = 216, com resto 0.
Exemplo 2: Divisão com Resto
Dividir 97 por 3.
Resultado: 97 ÷ 3 = 32, com resto 1.
Divisão com 2 ou mais algarismos no divisor
dividir com 2 algarismos no divisor, o processo é o mesmo, apenas temos que pensar que qualquer número pode ter a sua tabuada, por exemplo: 1235/15
Portanto 1235 dividido por 15 resulta em 82 e resto 5 Ps: sem preguiça de fazer a tabuada em
Divisão por 10, 100, 1000: Regras Práticas
Dividir números inteiros por potências de 10 (10, 100, 1000, etc.) é um processo simplificado que não exige o algoritmo da divisão longa. Basta observar a quantidade de zeros no divisor:
•Divisão por 10: Remove-se o último algarismo do dividendo. Este algarismo removido será o resto, e o número restante será o quociente. Se o dividendo terminar em 0, basta remover o 0 e o resto será 0.
•Ex: 250 ÷ 10 = 25 (resto 0)
•Ex: 253 ÷ 10 = 25 (resto 3)
•Divisão por 100: Removem-se os dois últimos algarismos do dividendo. Os algarismos removidos formam o resto, e o número restante é o quociente. Se o dividendo terminar em 00, o resto será 0.
•Ex: 1200 ÷ 100 = 12 (resto 0)
•Ex: 1234 ÷ 100 = 12 (resto 34)
•Divisão por 1000: Removem-se os três últimos algarismos do dividendo. Os algarismos removidos formam o resto, e o número restante é o quociente. Se o dividendo terminar em 000, o resto será 0.
•Ex: 5000 ÷ 1000 = 5 (resto 0)
•Ex: 5678 ÷ 1000 = 5 (resto 678)
Essas regras práticas são atalhos úteis para cálculos rápidos e para desenvolver uma intuição sobre a magnitude dos números.
Divisão com Resto
Em muitas situações da vida real e em problemas matemáticos, a divisão de um número inteiro por outro não resulta em um quociente exato. Nesses casos, temos uma divisão com resto, onde uma parte do dividendo não pode ser distribuída igualmente pelo divisor. Compreender o significado e a importância do resto é fundamental para interpretar corretamente os resultados de uma divisão.
Significado do Resto
O resto é a quantidade que "sobra" após a distribuição ou agrupamento. Ele representa a porção do dividendo que é menor que o divisor e, portanto, não pode ser dividida em mais partes inteiras pelo divisor. Por exemplo, se você tem 17 balões e quer fazer buquês com 5 balões cada, você fará 3 buquês completos (quociente) e sobrarão 2 balões (resto). Esses 2 balões não são suficientes para formar outro buquê de 5.
É importante notar que o resto é sempre um número inteiro e deve ser menor que o divisor. Se o resto for igual ou maior que o divisor, significa que a divisão não foi concluída corretamente e ainda é possível dividir mais. Por exemplo, se em uma divisão por 5 o resto fosse 6, isso indicaria um erro, pois o 5 ainda caberia uma vez no 6.
Relação entre Dividendo, Divisor, Quociente e Resto
A relação fundamental que conecta todos os elementos de uma divisão é expressa pela seguinte fórmula:
Dividendo (D) = Divisor (d) × Quociente (Q) + Resto (R)
Esta fórmula é uma ferramenta poderosa para verificar se uma divisão foi realizada corretamente. Se você multiplicar o quociente pelo divisor e somar o resto, o resultado deve ser igual ao dividendo original. Vamos usar o exemplo anterior de 17 ÷ 5:
•Dividendo (D) = 17
•Divisor (d) = 5
•Quociente (Q) = 3
•Resto (R) = 2
Aplicando a fórmula:
17 = 5 × 3 + 2 17 = 15 + 2 17 = 17
Como o resultado é verdadeiro, a divisão foi feita corretamente.
Exemplos de Aplicação: Situações Onde o Resto é Importante
O resto não é apenas um número que sobra; ele frequentemente carrega um significado prático importante no contexto do problema:
•Distribuição de Recursos: Se uma empresa tem 100 canetas para distribuir igualmente entre 12 funcionários, 100 ÷ 12 = 8 com resto 4. Isso significa que cada funcionário receberá 8 canetas, e sobrarão 4 canetas que não podem ser distribuídas igualmente. A empresa pode decidir guardar essas 4 canetas para uso futuro ou distribuí-las de outra forma.
•Planejamento de Eventos: Para organizar mesas com 6 cadeiras em um evento com 50 convidados, 50 ÷ 6 = 8 com resto 2. Serão necessárias 8 mesas completas, e sobrarão 2 convidados que precisarão de uma mesa adicional (mesmo que incompleta) ou de um arranjo diferente. O resto aqui indica a necessidade de uma ação extra.
•Ciclos e Repetições: Em problemas que envolvem ciclos, como dias da semana ou meses do ano, o resto pode indicar a posição dentro do ciclo. Por exemplo, se hoje é segunda-feira e queremos saber qual dia da semana será daqui a 100 dias, dividimos 100 por 7 (número de dias na semana): 100 ÷ 7 = 14 com resto 2. O resto 2 significa que serão 14 semanas completas mais 2 dias. Contando 2 dias a partir de segunda-feira, chegamos à quarta-feira.
•Cálculo de Pacotes ou Grupos: Se um produto é vendido em pacotes de 3 unidades e você precisa de 10 unidades, 10 ÷ 3 = 3 com resto 1. Você precisará comprar 4 pacotes (3 completos e 1 para a unidade restante), pois não é possível comprar apenas uma parte de um pacote. O resto, neste caso, influencia a decisão de compra.
Em resumo, o resto na divisão de números inteiros não é um mero descarte; ele é uma informação valiosa que complementa o quociente e fornece uma compreensão mais completa do resultado da operação em um contexto real. Ignorar o resto pode levar a conclusões erradas ou a decisões inadequadas.
Aplicações Práticas da Divisão no Cotidiano
A matemática, e a divisão em particular, não é apenas um conjunto de regras abstratas; ela é uma ferramenta poderosa que utilizamos constantemente em nosso dia a dia, muitas vezes sem perceber. A capacidade de dividir eficientemente é essencial para gerenciar finanças, planejar eventos, cozinhar e em muitas outras situações. Vejamos alguns exemplos práticos de como a divisão se manifesta em nosso cotidiano:
•Divisão de Contas: Ao sair com amigos para comer ou se divertir, é comum dividir a conta igualmente. Se a conta total foi de R150,00evoce^ssa~o5pessoas,adivisa~o(150÷5=30)rapidamenteinformaquecadaumdevepagarR 150,00 e vocês são 5 pessoas, a divisão (150 ÷ 5 = 30) rapidamente informa que cada um deve pagar R150,00evoce^ssa~o5pessoas,adivisa~o(150÷5=30)rapidamenteinformaquecadaumdevepagarR 30,00.
•Planejamento de Viagens: Se você está planejando uma viagem de 800 km e seu carro faz 10 km por litro de combustível, a divisão (800 ÷ 10 = 80) indica que você precisará de 80 litros de gasolina para a viagem. Se o tanque do seu carro tem capacidade para 40 litros, você sabe que precisará abastecer pelo menos duas vezes (80 ÷ 40 = 2).
•Receitas Culinárias: Muitas vezes, precisamos ajustar as quantidades de uma receita para servir mais ou menos pessoas. Se uma receita original serve 4 pessoas e pede 200g de farinha, e você quer servir 8 pessoas, você precisará dobrar a receita. Mas se quiser servir apenas 2 pessoas, você dividirá as quantidades pela metade. A divisão é fundamental para essa proporcionalidade.
•Orçamento Doméstico: Ao planejar o orçamento mensal, a divisão ajuda a alocar recursos. Se você tem um salário de R3.000,00equereconomizarR 3.000,00 e quer economizar R3.000,00equereconomizarR 500,00 por mês, a divisão pode ajudar a determinar quanto você pode gastar por dia ou por semana em diferentes categorias.
•Compras e Descontos: Ao comparar preços, a divisão é útil para calcular o preço por unidade ou por grama, permitindo identificar a melhor oferta. Por exemplo, se um pacote com 6 iogurtes custa R12,00,oprec\coporiogurteeˊR 12,00, o preço por iogurte é R12,00,oprec\coporiogurteeˊR 2,00 (12 ÷ 6). Se outro pacote com 4 iogurtes custa R9,00,oprec\coporiogurteeˊR 9,00, o preço por iogurte é R9,00,oprec\coporiogurteeˊR 2,25 (9 ÷ 4), indicando que o primeiro pacote é mais vantajoso.
•Esportes e Jogos: Em esportes, a divisão é usada para calcular médias de pontos, gols por partida, ou para dividir equipes de forma justa. Em jogos de tabuleiro, pode ser necessário dividir cartas ou peças igualmente entre os jogadores.
Esses são apenas alguns exemplos de como a divisão é uma habilidade matemática indispensável para a vida prática. Dominá-la não só facilita a resolução de problemas cotidianos, mas também desenvolve o raciocínio lógico e a capacidade de tomar decisões informadas.
Dicas e Estratégias para Dominar a Divisão
Dominar a divisão, assim como qualquer outra habilidade matemática, requer prática e uma abordagem estratégica. Aqui estão algumas dicas e estratégias que podem ajudar você a aprimorar suas habilidades em divisão:
•Compreenda os Conceitos, Não Apenas Memorize: Em vez de apenas memorizar o algoritmo da divisão, esforce-se para entender o que cada passo significa. Compreenda as diferentes interpretações da divisão (repartição, medida, inversa da multiplicação, subtrações sucessivas). Essa compreensão conceitual tornará a aplicação do algoritmo mais intuitiva.
•Domine a Multiplicação e a Subtração: A divisão longa depende fortemente de suas habilidades em multiplicação e subtração. Certifique-se de que você tem um bom domínio da tabuada e da subtração, pois isso agilizará o processo e reduzirá erros.
•Pratique Regularmente: A prática leva à perfeição. Comece com problemas simples e gradualmente aumente a complexidade. Resolva uma variedade de problemas, incluindo divisões exatas e com resto, e problemas contextualizados.
•Use Material de Apoio Visual: Para iniciantes, o uso de objetos físicos (como blocos, moedas, ou até mesmo desenhos) pode ajudar a visualizar o processo de repartição ou agrupamento, tornando o conceito mais concreto.
•Verifique Seus Resultados: Sempre que possível, use a relação entre divisão e multiplicação para verificar seus resultados. Multiplique o quociente pelo divisor e some o resto; o resultado deve ser o dividendo original. Isso ajuda a identificar erros e reforça a compreensão da operação.
•Divida Problemas Complexos em Partes Menores: Se você se deparar com um problema de divisão muito grande, tente dividi-lo em etapas menores e mais gerenciáveis. O algoritmo da divisão longa já faz isso naturalmente, mas a ideia pode ser aplicada a problemas mais amplos.
•Seja Paciente e Persistente: Aprender divisão pode levar tempo e exigir esforço. Não se desanime com os erros; eles são parte do processo de aprendizagem. Mantenha a paciência e a persistência, e você verá o progresso.
•Utilize Recursos Online e Aplicativos: Existem muitos recursos online, vídeos explicativos e aplicativos interativos que podem tornar o aprendizado da divisão mais divertido e eficaz. O site "Nossa Matemática" é um excelente ponto de partida!
Ao aplicar essas dicas, você não apenas melhorará sua capacidade de realizar divisões, mas também desenvolverá um raciocínio matemático mais aguçado e uma maior confiança em suas habilidades.
Conclusão
A divisão de números inteiros é muito mais do que uma simples operação aritmética; é uma habilidade fundamental que permeia diversas áreas da matemática e do nosso cotidiano. Ao longo deste guia, exploramos seus conceitos essenciais, como dividendo, divisor, quociente e resto, e diferenciamos a divisão exata da não exata. Mergulhamos nas diferentes interpretações da divisão – como repartição equitativa, medida, operação inversa da multiplicação e subtrações sucessivas – demonstrando a versatilidade e a profundidade dessa operação.
Detalhadamente, desvendamos o algoritmo da divisão longa, um método sistemático que, com prática, se torna uma ferramenta poderosa para resolver problemas de qualquer complexidade. Vimos também a importância do resto, não como uma mera sobra, mas como uma informação crucial que complementa o resultado da divisão e possui significado prático em diversas situações. As aplicações da divisão no dia a dia, desde a divisão de contas até o planejamento de viagens, reforçam sua relevância e a necessidade de dominá-la.
Esperamos que este guia tenha desmistificado a divisão para você, transformando o que antes poderia parecer um desafio em uma operação lógica e acessível. Lembre-se de que a prática constante, a compreensão dos conceitos e a paciência são as chaves para o domínio. Continue explorando, questionando e aplicando o que aprendeu. A matemática é uma jornada contínua de descobertas, e a divisão é um passo essencial nessa emocionante aventura. Continue praticando no "Nossa Matemática" e aprimore suas habilidades!


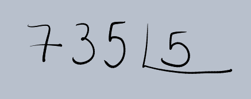
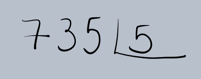
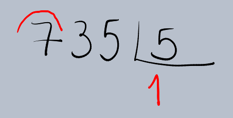
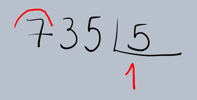

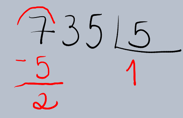
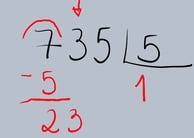
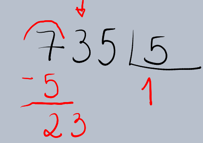
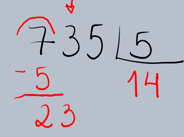
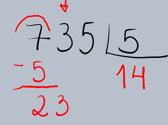
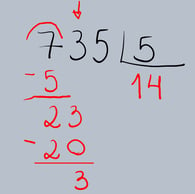
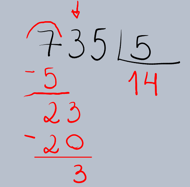
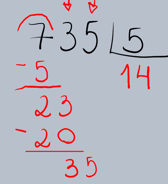
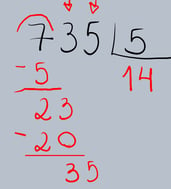
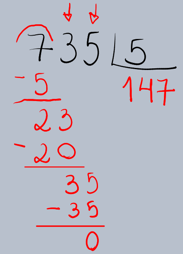
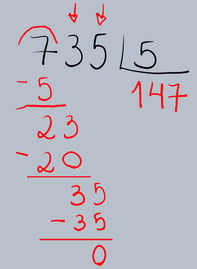
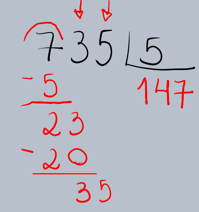
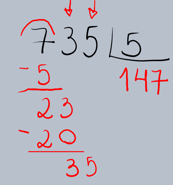
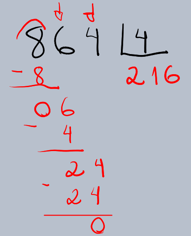

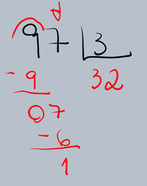
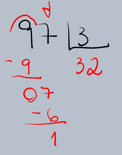
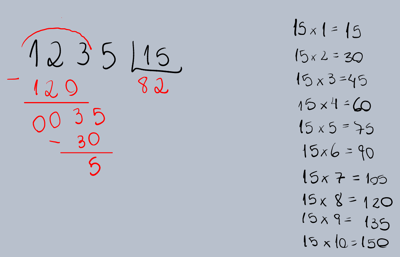
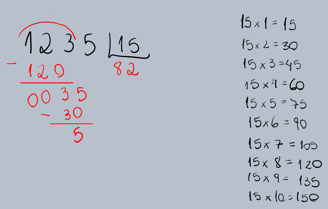
Algumas video-aulas sobre o assunto:
http://www.youtube.com/watch?v=nmXZiVVLRkk
Canal: Dicasdemat Sandro Curió
http://www.youtube.com/watch?v=aLbGmmmcra8
Canal: Matemática com Alê
