A Base de Tudo – O Que São Conjuntos Numéricos?

Na matemática, os conjuntos numéricos são como os blocos de construção de todo o edifício teórico. Eles representam agrupamentos de números que compartilham características específicas, permitindo-nos organizar e compreender a vasta gama de números que utilizamos. Desde a simples contagem dos dedos até os cálculos mais complexos da engenharia e da física, os conjuntos numéricos estão sempre presentes.

Imagine que você está organizando diferentes tipos de objetos em caixas. Cada caixa representa um conjunto, e os objetos dentro dela (os números) possuem algo em comum. Entender essas "caixas" e seus conteúdos é o primeiro passo para dominar a linguagem da matemática. Nesta postagem, faremos uma viagem detalhada por cada um dos principais conjuntos numéricos, explorando suas peculiaridades e como eles se relacionam entre si.

1. O Conjunto dos Números Naturais (ℕ): Contando o Mundo ao Nosso Redor

O primeiro conjunto que geralmente encontramos é o dos números naturais, representado pelo símbolo ℕ. Estes são os números que usamos para contar objetos: 0, 1, 2, 3, 4, 5, e assim por diante. A grande maioria das definições modernas inclui o zero como um número natural, representando a ausência de quantidade.

Características Principais dos Naturais:

• Infinito: Não existe um último número natural. Sempre podemos adicionar 1 a qualquer número natural e obter outro.

• Discreto: Entre dois números naturais consecutivos, não existe outro número natural. Por exemplo, entre 3 e 4, não há outro número natural.

• Operações Fechadas: A adição e a multiplicação de dois números naturais sempre resultam em outro número natural. (Ex: 2 + 3 = 5 ∈ ℕ; 2 × 3 = 6 ∈ ℕ).

Os números naturais são a base da aritmética e da contagem, sendo essenciais em diversas aplicações do nosso dia a dia, desde contar moedas até indexar itens em uma lista.

2. O Conjunto dos Números Inteiros (ℤ): Expandindo para o Negativo

O conjunto dos números inteiros, denotado por ℤ (da palavra alemã "Zahl", que significa número), surge da necessidade de representar quantidades negativas, como débitos, temperaturas abaixo de zero ou profundidades abaixo do nível do mar. Ele inclui todos os números naturais e seus opostos negativos: ..., -3, -2, -1, 0, 1, 2, 3, ....

Características Principais dos Inteiros:

• Infinito: O conjunto dos inteiros é infinito tanto na direção positiva quanto na negativa.

• Discreto: Assim como os naturais, os inteiros são discretos.

• Operações Fechadas: A adição, a subtração e a multiplicação de dois números inteiros sempre resultam em outro número inteiro. (Ex: 5 - 8 = -3 ∈ ℤ).

Os números inteiros são cruciais na álgebra e na resolução de equações que envolvem resultados negativos.

3. O Conjunto dos Números Racionais (ℚ): A Arte das Frações

O conjunto dos números racionais, representado por ℚ (de "quociente"), é formado por todos os números que podem ser expressos como uma fração ba​, onde a e b são números inteiros e b é diferente de zero. Isso inclui tanto os números inteiros (quando b=1) quanto as frações propriamente ditas, como 21​, −43​, 57​, etc.

Características Principais dos Racionais:

• Infinito: O conjunto dos racionais é infinito.

• Denso: Entre quaisquer dois números racionais distintos, sempre existe outro número racional. Podemos sempre encontrar a média entre eles, que também será um número racional.

• Representação Decimal: A representação decimal de um número racional é sempre finita (ex: 0.5 = 21​) ou infinita e periódica (ex: 0.333... = 31​).

• Operações Fechadas: A adição, a subtração, a multiplicação e a divisão (por um número racional não nulo) de dois números racionais sempre resultam em outro número racional.

Os números racionais são essenciais para representar medidas precisas, proporções e probabilidades.

4. O Conjunto dos Números Irracionais (𝕀): Além da Razão

O conjunto dos números irracionais, denotado por 𝕀 (algumas vezes também representado por R∖Q), compreende todos os números reais que não podem ser expressos como uma fração de dois inteiros. Sua característica marcante é a representação decimal infinita e não periódica.

Características Principais dos Irracionais:

• Infinito: O conjunto dos irracionais é infinito.

• Representação Decimal: Sua representação decimal nunca termina e não possui um padrão de repetição.

• Exemplos Clássicos: 2​ (raiz quadrada de 2, aproximadamente 1.41421356...), π (pi, a razão entre a circunferência de um círculo e seu diâmetro, aproximadamente 3.14159...), e e (o número de Euler, aproximadamente 2.71828...) são exemplos bem conhecidos de números irracionais.

Os números irracionais surgem naturalmente em geometria (como π) e em diversas áreas da matemática e da física.

5. O Conjunto dos Números Reais (ℝ): A União de Todos

O conjunto dos números reais, simbolizado por ℝ, é a união do conjunto dos números racionais (ℚ) com o conjunto dos números irracionais (𝕀). Ele representa todos os pontos em uma linha numérica contínua, abrangendo todas as formas de números que encontramos até agora.

Características Principais dos Reais:

• Infinito: O conjunto dos reais é infinito.

• Contínuo: Ao contrário dos racionais, os reais formam um conjunto contínuo, sem "lacunas". Entre quaisquer dois números reais distintos, existem infinitos outros números reais.

• Ordenação: Os números reais podem ser ordenados de forma linear.

• Completude: Uma propriedade fundamental dos números reais é a completude, que garante a existência de limites de sequências e a ausência de "buracos" na reta numérica.

Os números reais são a base do cálculo diferencial e integral, da análise real e de muitas aplicações em ciências e engenharia.

6. O Conjunto dos Números Complexos (ℂ): Expandindo para a Imaginação

O conjunto dos números complexos, denotado por ℂ, expande o conceito de números para além da reta numérica, introduzindo a unidade imaginária i, definida como a raiz quadrada de -1 (i=−1​). Um número complexo é geralmente expresso na forma a+bi, onde a e b são números reais, a é a parte real e b é a parte imaginária.

Características Principais dos Complexos:

• Infinito: O conjunto dos complexos é infinito.

• Plano Complexo: Os números complexos podem ser representados em um plano bidimensional, conhecido como plano complexo ou plano de Argand-Gauss.

• Operações Fechadas: As operações de adição, subtração, multiplicação e divisão (por um número complexo não nulo) são fechadas no conjunto dos números complexos.

• Teorema Fundamental da Álgebra: Um resultado importante é o Teorema Fundamental da Álgebra, que afirma que todo polinômio de grau n≥1 com coeficientes complexos possui exatamente n raízes complexas.

Os números complexos são cruciais em áreas como eletricidade e magnetismo, mecânica quântica e processamento de sinais.

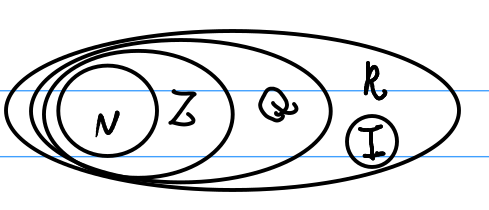
Relações e Hierarquia entre os Conjuntos Numéricos

É importante entender como esses conjuntos se relacionam entre si. Podemos visualizar essa relação como uma hierarquia de inclusão:

N⊂Z⊂Q⊂R⊂C

Isso significa que todo número natural é também um número inteiro, todo número inteiro é também um número racional, todo número racional é também um número real, 1 e todo número real é também um número complexo (onde a parte imaginária é zero)

Conclusão: Dominando a Linguagem dos Números

Compreender os conjuntos numéricos é fundamental para construir uma base sólida em matemática. Cada conjunto possui suas próprias características e propriedades, e a forma como eles se relacionam é essencial para avançar em estudos mais complexos. Espero que esta exploração detalhada e didática tenha tornado este tema mais acessível e interessante para você. Continue explorando o fascinante mundo da matemática!

Algumas video-aulas sobre o assunto:

https://youtu.be/6d9-kgWigmo?si=vs139Y_skX7OQGjd

Canal: Gis com Giz da Matemática

https://youtu.be/RrjtgevcYjw?si=LbIcxxcslGHXa92s

Canal: Dicasdemat Sandro Curió