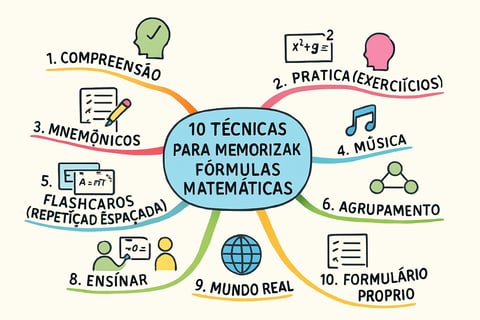
As 10 Técnicas Infalíveis para Dominar as Fórmulas Matemáticas
Anderson Luiz Floriano Dos Santos
5/28/202518 min read
10 Técnicas Eficazes para Memorizar Fórmulas Matemáticas e Conquistar a Aprovação
Introdução: Desvendando o 'Bicho-Papão' das Fórmulas Matemáticas
A matemática. Para muitos estudantes, especialmente aqueles que se preparam para concursos ou enfrentam os desafios do ensino fundamental e médio, essa palavra pode evocar uma mistura de respeito e apreensão. E, dentro desse universo de números e operações, as fórmulas matemáticas frequentemente surgem como um dos maiores obstáculos. Quem nunca se sentiu perdido em meio a um emaranhado de letras, símbolos e números que parecem desafiar a lógica e a memória?
Seja a fórmula de Bhaskara, o teorema de Pitágoras, as relações trigonométricas ou as complexas equações da física (que também usam a linguagem matemática), a necessidade de memorizar essas ferramentas é inegável. Elas são as chaves que abrem as portas para a resolução de problemas, a compreensão de conceitos e, crucialmente, para o sucesso em provas e avaliações importantes. Concurseiros sabem bem: dominar as fórmulas certas no momento certo pode ser a diferença entre a aprovação e mais um ano de estudos.
Mas será que memorizar fórmulas precisa ser um processo doloroso e frustrante? A resposta é um sonoro não! O cérebro humano, essa máquina incrível que possuímos, tem uma capacidade fantástica de aprender e reter informações, desde que utilizemos as estratégias corretas. Esquecer aquela fórmula crucial no meio da prova não precisa ser o seu destino.
Neste artigo completo, preparado especialmente para você, estudante do ensino fundamental, médio ou concurseiro dedicado, vamos desmistificar a memorização de fórmulas matemáticas. Apresentaremos 10 técnicas eficazes, comprovadas e acessíveis, que transformarão sua relação com a matemática. Esqueça a decoreba pura e simples; vamos focar em métodos que envolvem compreensão, associação, criatividade e organização.
Ao longo deste guia, você descobrirá como:
Entender a lógica por trás das fórmulas para uma memorização mais profunda.
Utilizar a prática de exercícios como uma ferramenta poderosa de fixação.
Criar associações divertidas com mnemônicos e músicas.
Organizar visualmente as informações com mapas mentais.
Implementar sistemas de revisão que combatem a curva do esquecimento.
Nosso objetivo é fornecer um arsenal completo de estratégias para que você não apenas memorize, mas compreenda e internalize as fórmulas matemáticas, tornando-as suas aliadas na jornada do aprendizado e na busca pela aprovação. Prepare-se para turbinar sua memória e encarar a matemática com muito mais confiança e segurança. Vamos começar?
Por Que Simplesmente Decorar Não Funciona (ou Funciona Mal)?
Antes de mergulharmos nas técnicas eficazes, é fundamental entender por que a abordagem tradicional de
simplesmente 'decorar' muitas vezes falha a longo prazo, especialmente no contexto da matemática.
A memorização mecânica, ou 'decoreba', baseia-se na repetição exaustiva sem uma conexão real com o significado ou a aplicação do que está sendo memorizado. É como tentar guardar um número de telefone aleatório sem associá-lo a uma pessoa ou lugar. Pode funcionar por um curto período, talvez até a véspera da prova, mas a informação tende a se dissipar rapidamente da memória.
As Limitações da Decoreba:
Falta de Compreensão Profunda: Decorar uma fórmula sem entender por que ela funciona, de onde ela vem ou como se relaciona com outros conceitos matemáticos cria uma base de conhecimento frágil. Se o problema apresentado na prova for ligeiramente diferente do exemplo que você decorou, a fórmula memorizada pode se tornar inútil, pois você não saberá como adaptá-la ou aplicá-la corretamente.
Esquecimento Rápido: A famosa 'curva do esquecimento', estudada pelo psicólogo Hermann Ebbinghaus, demonstra que tendemos a esquecer rapidamente informações que não são reforçadas por significado ou revisão espaçada. Fórmulas decoradas sem contexto são candidatas perfeitas a serem esquecidas sob a pressão de um exame.
Sobrecarga Cognitiva: Tentar enfiar dezenas de fórmulas na cabeça sem critério ou conexão sobrecarrega a memória de curto prazo. Isso não apenas dificulta a retenção das próprias fórmulas, mas também pode prejudicar a capacidade de raciocínio e resolução de problemas durante a prova.
Falta de Transferência de Conhecimento: O conhecimento verdadeiramente útil é aquele que pode ser transferido e aplicado em diferentes situações. Fórmulas apenas decoradas raramente permitem essa flexibilidade. O aluno pode saber recitar a fórmula, mas não consegue usá-la para resolver um problema do mundo real ou conectá-la a um novo conceito.
Gera Ansiedade e Frustração: A dependência da decoreba pode gerar grande ansiedade. O medo constante de 'dar um branco' e esquecer a fórmula exata no momento H é paralisante para muitos estudantes. Além disso, o esforço repetitivo sem a recompensa da compreensão genuína leva à frustração e a uma visão negativa da matemática.
O Caminho Alternativo: Memorização com Significado
As técnicas que apresentaremos a seguir buscam justamente superar essas limitações. Elas se baseiam em princípios de aprendizagem mais eficazes, que envolvem:
Conexão: Associar a fórmula a conceitos já conhecidos, à sua origem ou a exemplos práticos.
Visualização: Usar imagens, diagramas ou mapas mentais para representar a informação.
Elaboração: Explicar a fórmula com suas próprias palavras, ensiná-la a outra pessoa ou criar exemplos.
Aplicação: Usar a fórmula repetidamente em contextos variados (resolução de exercícios).
Organização: Agrupar fórmulas relacionadas ou criar sistemas lógicos de memorização.
Ao adotar essas abordagens, você não estará apenas 'guardando' a fórmula na memória, mas construindo uma compreensão sólida que permitirá recuperá-la e aplicá-la com confiança quando necessário. Agora sim, vamos às 10 técnicas que revolucionarão sua forma de lidar com as fórmulas matemáticas!
As 10 Técnicas Infalíveis para Dominar as Fórmulas Matemáticas
Chegou a hora de conhecer as estratégias que farão a diferença nos seus estudos. Lembre-se que a combinação de diferentes técnicas pode ser ainda mais poderosa. Experimente e descubra quais funcionam melhor para você!
Técnica 1: Entenda a Fórmula Antes de Tudo (A Base Sólida)
Pode parecer contraintuitivo começar uma jornada de memorização falando em compreensão, mas esta é, sem dúvida, a técnica mais fundamental e negligenciada. Como mencionamos, decorar algo sem entender seu propósito é como construir uma casa sem alicerces: ela pode até ficar de pé por um tempo, mas desmoronará ao menor sinal de dificuldade.
Como Aplicar:
Não Pule a Teoria: Antes de partir para a fórmula em si, dedique tempo para entender o conceito matemático que ela representa. Qual problema ela resolve? Qual fenômeno ela descreve?
Investigue a Origem (se possível): Algumas fórmulas têm histórias interessantes ou derivam de princípios mais básicos. Conhecer a dedução da fórmula de Bhaskara a partir da completação de quadrados, por exemplo, pode solidificar seu entendimento e facilitar a memorização.
Identifique Cada Componente: O que significa cada letra ou símbolo na fórmula? Qual unidade de medida está associada a cada variável (especialmente em física)? Entender o papel de cada 'peça' torna o todo mais lógico.
Verbalize a Fórmula: Tente explicar a fórmula com suas próprias palavras. Se você consegue explicar o que ela faz e o que cada parte significa, você está no caminho certo da compreensão.
Conecte com Exemplos Práticos: Como essa fórmula se aplica em situações reais ou em problemas concretos? A fórmula da área do círculo (A = πr²) fica mais fácil de lembrar quando você a associa ao cálculo da área de uma pizza ou de um terreno circular.
Por que Funciona? Nosso cérebro é programado para buscar significado. Informações conectadas a um contexto lógico e a conhecimentos prévios são processadas e armazenadas de forma muito mais eficiente e duradoura na memória de longo prazo. Entender a fórmula transforma-a de uma sequência abstrata de símbolos em uma ferramenta com propósito.
Técnica 2: A Prática Leva à Fixação (Repetição Inteligente)
A máxima "a prática leva à perfeição" é especialmente verdadeira quando se trata de fórmulas matemáticas. No entanto, não estamos falando de copiar a fórmula dezenas de vezes sem pensar, mas sim de aplicá-la ativamente na resolução de problemas.
Como Aplicar:
Resolva Muitos Exercícios: Esta é a forma mais direta de praticar. Quanto mais você usar uma fórmula para resolver diferentes tipos de questões, mais natural ela se tornará.
Comece com o Básico: Inicie com exercícios simples que exijam apenas a aplicação direta da fórmula. Isso ajuda a familiarizar-se com sua estrutura e componentes.
Aumente a Complexidade Gradualmente: Avance para problemas que combinem a fórmula com outros conceitos, exijam manipulação algébrica ou apresentem contextos mais elaborados. Isso força você a pensar sobre a fórmula de maneira mais profunda.
Varie os Tipos de Problemas: Não resolva apenas exercícios do mesmo estilo. Procure questões de múltipla escolha, discursivas, problemas aplicados, desafios, etc. A variedade expõe diferentes facetas da aplicação da fórmula.
Refaça Exercícios Errados: Ao corrigir seus erros, preste atenção especial em como a fórmula deveria ter sido aplicada. Refazer esses exercícios é crucial para corrigir equívocos e reforçar o aprendizado.
Use a Fórmula Ativamente: Ao resolver um exercício, evite consultar a fórmula imediatamente. Tente recuperá-la da memória primeiro. Só consulte se realmente não conseguir lembrar. Esse esforço de recuperação fortalece as conexões neurais.
Por que Funciona? A resolução de exercícios funciona como uma forma de repetição espaçada e contextualizada. Cada vez que você aplica a fórmula, você reforça o caminho neural associado a ela. Além disso, a prática em diferentes contextos ajuda a entender as nuances da sua aplicação e a solidificar a compreensão (conectando-se à Técnica 1).
Técnica 3: Mnemônicos Criativos (Associações Divertidas)
Os mnemônicos são ferramentas de memorização poderosas que utilizam associações (muitas vezes engraçadas, inusitadas ou rítmicas) para facilitar a lembrança de informações sequenciais ou complexas, como as fórmulas.
Como Aplicar:
Frases Engraçadas ou Significativas: Crie uma frase onde as iniciais das palavras (ou sílabas) correspondam aos elementos da fórmula. Quanto mais pessoal ou absurda a frase, mais fácil pode ser lembrá-la.
Exemplo Clássico (Trigonometria no Triângulo Retângulo): Para as relações seno (cateto Oposto / Hipotenusa), cosseno (cateto Adjacente / Hipotenusa) e tangente (cateto Oposto / cateto Adjacente), a frase "Corri A Hora que O Homem Caiu" ou o "SOH CAH TOA" (em inglês) são mnemônicos famosos. Outra versão: "Com Alguma Habilidade, Olhei Hoje, Tomei Outra Atitude".
Exemplo (Lei de Euler para Poliedros): V + F = A + 2. Frase: "Vamos Fazer Amor a 2" (um clássico dos cursinhos).
Exemplo (Equação da Reta): y – y₀ = m(x – x₀). Frase: "YoYô – MiXoXô".
Acrônimos: Forme uma palavra (que pode ou não existir) com as iniciais dos elementos da fórmula.
Histórias Curtas: Crie uma pequena narrativa que incorpore os elementos da fórmula em sequência.
Associações Visuais: Imagine uma cena ou objeto bizarro que represente a fórmula.
Dicas para Criar Bons Mnemônicos:
Seja Pessoal: Mnemônicos que você mesmo cria tendem a ser mais eficazes.
Use Humor e Exagero: O cérebro lembra melhor de coisas fora do comum.
Incorpore Imagens Mentais Vívidas: Quanto mais sensorial (visual, auditivo) for o mnemônico, melhor.
Mantenha Simples: Mnemônicos muito complexos podem ser mais difíceis de lembrar do que a própria fórmula.
Por que Funciona? Mnemônicos funcionam porque conectam informações novas e abstratas (a fórmula) a informações já existentes e mais concretas (palavras, imagens, histórias) na sua memória. Eles criam 'ganchos' mentais que facilitam a recuperação da informação desejada.
(Continua...)
Técnica 4: Transforme Fórmulas em Música (O Ritmo da Memória)
Se você tem uma veia musical ou simplesmente acha mais fácil lembrar de letras de música do que de definições, esta técnica é para você! Transformar fórmulas matemáticas em paródias de músicas conhecidas ou criar pequenos jingles pode ser uma maneira extremamente eficaz e divertida de fixá-las na memória.
Como Aplicar:
Escolha uma Melodia Familiar: Pegue uma música popular, um jingle de comercial, uma cantiga de roda ou qualquer melodia que já esteja "grudada" na sua cabeça.
Adapte a Letra: Reescreva a letra da música para incorporar os elementos da fórmula na ordem correta. Tente manter o ritmo e a métrica da melodia original.
Seja Criativo e Repetitivo: Não tenha medo de ser bobo ou exagerado. Cante sua paródia várias vezes, no chuveiro, no ônibus, enquanto estuda. A repetição cantada ajuda a automatizar a lembrança.
Grave e Ouça: Se possível, grave sua criação e ouça-a periodicamente, como faria com suas músicas favoritas.
Exemplo (Fórmula de Bhaskara): Imagine pegar uma melodia simples e cantar algo como: "Para achar o xis / Que me deixa feliz / Uso menos b, mais ou menos raiz / De delta sobre dois a / E o delta, quem será? / É b ao quadrado menos quatro a c!". (Adapte à melodia que preferir!)
Por que Funciona? A música ativa múltiplas áreas do cérebro, incluindo as ligadas à emoção e à memória de longo prazo. O ritmo e a melodia funcionam como estruturas que "carregam" a informação da fórmula, tornando-a mais fácil de recordar do que uma sequência abstrata de símbolos. Além disso, o processo criativo de fazer a paródia já é, por si só, uma forma de estudo ativo.
Técnica 5: Flashcards e Repetição Espaçada (Combate ao Esquecimento)
Flashcards são cartões simples (físicos ou digitais) que ajudam a testar ativamente sua memória. Combinados com a técnica da repetição espaçada (revisar a informação em intervalos crescentes de tempo), eles se tornam uma ferramenta poderosa contra a curva do esquecimento.
Como Aplicar:
Crie seus Flashcards:
Frente: Escreva o nome da fórmula (ex: "Área do Trapézio") ou um problema/conceito que a utilize (ex: "Como calcular a energia cinética?").
Verso: Escreva a fórmula completa (ex: A = (B+b)h/2) ou a fórmula e uma breve explicação/aplicação (ex: Ec = mv²/2, onde m é massa e v é velocidade).
Teste-se Regularmente: Pegue um cartão, leia a frente e tente lembrar a fórmula no verso. Verifique sua resposta. Separe os cartões que acertou dos que errou.
Implemente a Repetição Espaçada:
Revisão Imediata: Revise os cartões que errou imediatamente.
Intervalos Crescentes: Revise os cartões que acertou em intervalos crescentes. Por exemplo:
Revisão 1: No dia seguinte.
Revisão 2: Daqui a 3 dias.
Revisão 3: Daqui a 1 semana.
Revisão 4: Daqui a 2 semanas.
E assim por diante...
Se errar um cartão em alguma revisão, ele volta para o início do ciclo (revisão no dia seguinte).
Use Ferramentas Digitais: Aplicativos como Anki, Quizlet ou Brainscape automatizam o sistema de repetição espaçada, tornando o processo mais prático.
Por que Funciona? O ato de tentar recuperar a informação da memória (teste ativo) é muito mais eficaz para a aprendizagem do que a simples releitura. A repetição espaçada baseia-se na forma como nossa memória funciona, reforçando as conexões neurais pouco antes de começarmos a esquecer a informação, otimizando a retenção a longo prazo com menos esforço ao longo do tempo.
Técnica 6: Agrupamento e Categorização (Organizando o Conhecimento)
Nossa mente adora organização. Tentar memorizar uma lista longa e desordenada de fórmulas é uma tarefa árdua. Agrupar fórmulas semelhantes ou relacionadas por tema, aplicação ou estrutura pode facilitar enormemente o processo de memorização e compreensão.
Como Aplicar:
Identifique Relações: Procure por fórmulas que pertençam à mesma área da matemática (ex: todas as fórmulas de área de figuras planas, todas as fórmulas de cinemática, todas as identidades trigonométricas).
Crie Categorias Lógicas: Organize as fórmulas em grupos que façam sentido para você. Pode ser por:
Tópico: Geometria Plana, Geometria Espacial, Álgebra, Trigonometria, Cinemática, Dinâmica, etc.
Tipo de Problema: Fórmulas para calcular áreas, volumes, velocidades, forças, etc.
Estrutura Similar: Fórmulas que compartilham variáveis ou operações semelhantes.
Use Recursos Visuais: Crie tabelas, diagramas ou até mesmo os mapas mentais (que veremos a seguir) para visualizar esses agrupamentos.
Compare e Contraste: Ao agrupar, analise as semelhanças e diferenças entre as fórmulas dentro de um mesmo grupo. Por que a fórmula da área do retângulo (A = bh) é diferente da do triângulo (A = bh/2)? Entender essas conexões reforça a memória.
Exemplo: Em vez de decorar isoladamente as fórmulas de juros simples (J = Cit) e juros compostos (M = C*(1+i)^t), agrupe-as na categoria "Matemática Financeira" e compare como o capital (C), a taxa (i) e o tempo (t) influenciam o resultado em cada regime de juros.
Por que Funciona? Agrupar informações cria uma estrutura mental que facilita o armazenamento e a recuperação. É como organizar arquivos em pastas no computador em vez de deixá-los todos soltos na área de trabalho. Ao lembrar de uma fórmula do grupo, fica mais fácil acessar as outras relacionadas. Além disso, a categorização promove uma compreensão mais profunda das relações entre diferentes conceitos matemáticos.
Técnica 7: Mapas Mentais e Visualizações (Desenhando a Memória)
Para muitos, o aprendizado visual é extremamente poderoso. Mapas mentais e outras formas de visualização transformam listas lineares de fórmulas em diagramas coloridos, organizados e interconectados, aproveitando a capacidade do cérebro de processar informações visuais de forma eficiente.
Como Aplicar:
Crie Mapas Mentais:
Centro: Escreva o tópico principal (ex: "Fórmulas de Geometria Plana") no centro de uma folha de papel (ou use um software de mapa mental).
Ramos Principais: Crie ramos saindo do centro para cada subcategoria ou fórmula principal (ex: "Áreas", "Perímetros").
Ramos Secundários: Detalhe cada ramo com as fórmulas específicas, seus componentes, exemplos ou mnemônicos.
Use Cores e Imagens: Utilize cores diferentes para cada ramo, adicione pequenos desenhos ou símbolos que representem os conceitos. Isso torna o mapa mais atraente e memorável.
[Espaço para Mapa Mental - Exemplo: Geometria Plana] (Aqui seria inserida a imagem do mapa mental criado)
Desenhe Diagramas: Para fórmulas que descrevem processos ou relações espaciais (como o Teorema de Pitágoras ou as leis de Newton), desenhar um diagrama que ilustre a situação física ou geométrica pode ser muito útil.
Use Cores e Destaques: Ao anotar fórmulas em seu caderno, use canetas coloridas, marca-textos ou caixas para destacar partes importantes, variáveis ou relações.
Visualize Mentalmente: Feche os olhos e tente visualizar a fórmula, seu mapa mental associado ou o diagrama que a representa. A visualização mental ativa as mesmas áreas cerebrais que a visualização real.
Por que Funciona? Mapas mentais espelham a forma como nosso cérebro organiza informações – através de associações e conexões radiais, e não de forma linear. Eles permitem ver o "quadro geral" e os detalhes simultaneamente. O uso de cores, imagens e estrutura espacial cria múltiplos gatilhos de memória, tornando a informação mais robusta e fácil de acessar. Para concurseiros e estudantes que lidam com grande volume de informação, os mapas mentais são aliados poderosos na organização e revisão.
(Continua...)
Técnica 8: Ensinar para Aprender (A Técnica Feynman Simplificada)
Uma das maneiras mais eficazes de verificar se você realmente entendeu e memorizou algo é tentar ensinar isso a outra pessoa. A famosa Técnica Feynman, atribuída ao físico Richard Feynman, baseia-se nesse princípio: se você não consegue explicar um conceito de forma simples, você provavelmente não o entendeu bem o suficiente.
Como Aplicar:
Escolha uma Fórmula ou Conceito: Selecione a fórmula que você está tentando memorizar.
Finja Ensinar (ou Ensine de Verdade!): Explique a fórmula em voz alta, como se estivesse ensinando para um colega, um familiar ou até mesmo para uma criança (o que força uma simplificação ainda maior). Descreva o que ela faz, o que cada parte significa e como usá-la.
Identifique as Lacunas: Preste atenção aos momentos em que você hesita, se confunde ou não consegue encontrar palavras simples. Essas são as áreas onde seu entendimento (e, consequentemente, sua memorização) ainda está fraco.
Volte ao Material Original: Consulte seus livros, anotações ou outras fontes para preencher essas lacunas e solidificar seu conhecimento.
Simplifique e Refine: Tente explicar novamente, usando analogias, exemplos mais simples e uma linguagem clara. Repita o processo até conseguir explicar a fórmula de forma fluida e compreensível.
Escreva a Explicação: Colocar sua explicação no papel também ajuda a organizar as ideias e reforçar a memória.
Por que Funciona? Ensinar força você a organizar seus pensamentos, identificar os pontos-chave de um conceito e traduzi-lo para uma linguagem acessível. Esse processo de recuperação ativa, simplificação e reestruturação da informação cria conexões neurais muito mais fortes do que a simples leitura passiva. Além disso, ao identificar suas próprias dificuldades durante a explicação, você sabe exatamente onde precisa focar seus estudos.
Técnica 9: Conecte com o Mundo Real (A Matemática Viva)
Fórmulas matemáticas podem parecer abstratas e distantes da realidade, mas muitas delas têm aplicações diretas no nosso dia a dia ou em fenômenos que observamos. Conectar as fórmulas a essas aplicações práticas torna-as mais tangíveis, interessantes e, consequentemente, mais fáceis de memorizar.
Como Aplicar:
Busque Aplicações Práticas: Pesquise ou pergunte ao seu professor como a fórmula que você está estudando é usada no mundo real.
Exemplo: A fórmula do juros compostos não serve apenas para a prova, mas rege investimentos, financiamentos e até o crescimento de populações.
Exemplo: As fórmulas de cinemática (velocidade, aceleração) descrevem o movimento de carros, o lançamento de objetos, etc.
Exemplo: As fórmulas de geometria são usadas em arquitetura, design, engenharia e até para calcular a quantidade de tinta necessária para pintar uma parede.
Crie Seus Próprios Exemplos: Pense em situações do seu cotidiano onde a fórmula poderia ser aplicada, mesmo que de forma simplificada.
Relacione com Outras Disciplinas: Veja como as fórmulas matemáticas aparecem na Física, Química, Biologia, Geografia ou Economia. Essa interdisciplinaridade reforça a relevância e a aplicabilidade do conhecimento.
Assista a Documentários ou Vídeos: Existem muitos recursos visuais que mostram a matemática em ação na natureza, na tecnologia e na sociedade.
Por que Funciona? Nosso cérebro tende a dar mais importância e a reter melhor informações que percebemos como relevantes e aplicáveis à nossa vida. Ao conectar uma fórmula abstrata a um contexto real e significativo, você cria mais um "gancho" para a memória e aumenta sua motivação para aprendê-la. A fórmula deixa de ser apenas uma exigência escolar e se torna uma ferramenta para entender o mundo.
Técnica 10: Crie Seu Próprio Formulário (Condensação e Revisão Ativa)
À medida que você avança nos estudos, a quantidade de fórmulas a serem lembradas pode se tornar esmagadora. Criar seu próprio formulário personalizado, um resumo organizado das fórmulas mais importantes, é uma excelente técnica de revisão ativa e condensação do conhecimento.
Como Aplicar:
Selecione as Fórmulas Essenciais: Não inclua absolutamente todas as fórmulas, mas sim aquelas que são fundamentais para cada tópico ou que você tem mais dificuldade em lembrar.
Organize de Forma Lógica: Use os princípios da Técnica 6 (Agrupamento e Categorização) para organizar seu formulário. Agrupe por matéria, por tipo de problema, etc.
Escreva à Mão (se possível): O ato físico de escrever ajuda na memorização. Use cores, símbolos e diagramas (como mini mapas mentais) para tornar seu formulário visualmente atraente e informativo.
Inclua Dicas e Mnemônicos: Ao lado de cada fórmula, anote um breve lembrete sobre sua aplicação, um mnemônico associado (Técnica 3) ou uma pequena visualização (Técnica 7).
Revise Ativamente: Não use o formulário apenas para consulta passiva. Use-o como um guia para testar sua memória:
Cubra as fórmulas e tente recitá-las a partir dos nomes ou categorias.
Use-o como base para criar flashcards (Técnica 5).
Tente recriar partes do formulário de memória.
Atualize Regularmente: À medida que aprende novas fórmulas ou domina as antigas, atualize seu formulário. Ele deve ser um documento vivo que reflete seu progresso.
Por que Funciona? O processo de criar o formulário já é um estudo ativo: você precisa selecionar, organizar, condensar e reescrever as informações. Isso força uma revisão profunda do material. Ter um resumo conciso e personalizado facilita as revisões rápidas e direcionadas, especialmente antes das provas. É a sua "cola" pessoal, construída com seu próprio esforço e entendimento.
Conclusão: A Memorização como Aliada, Não como Vilã
Chegamos ao fim da nossa jornada pelas 10 técnicas eficazes para memorizar fórmulas matemáticas. Esperamos que, a esta altura, você perceba que memorizar não precisa ser sinônimo de sofrimento ou de decoreba sem sentido. Pelo contrário, quando abordada com as estratégias certas, a memorização se torna uma consequência natural da compreensão e da prática inteligente.
Lembre-se das chaves que abrimos ao longo deste artigo:
Compreensão Primeiro: Entenda a lógica e o propósito da fórmula.
Prática Constante: Resolva exercícios variados para fixar a aplicação.
Mnemônicos Criativos: Use frases e associações divertidas.
Música e Ritmo: Transforme fórmulas em paródias ou jingles.
Flashcards e Repetição Espaçada: Teste sua memória e revise em intervalos crescentes.
Agrupamento Lógico: Organize as fórmulas por categorias.
Mapas Mentais Visuais: Desenhe diagramas coloridos e conectados.
Ensine para Aprender: Explique a fórmula com suas próprias palavras.
Conexão com o Mundo Real: Encontre aplicações práticas.
Formulário Personalizado: Crie seu próprio resumo ativo.
O segredo não está em usar apenas uma técnica isolada, mas em combinar aquelas que melhor se adaptam ao seu estilo de aprendizagem. Experimente, misture, adapte. Talvez você descubra que criar um mapa mental (Técnica 7) com mnemônicos (Técnica 3) e revisá-lo com flashcards (Técnica 5) seja a sua fórmula do sucesso!
Para você, concurseiro, que enfrenta uma vasta quantidade de conteúdo, e para você, estudante do ensino fundamental e médio, que está construindo as bases do seu conhecimento matemático, dominar essas técnicas significa ganhar confiança, agilidade e segurança. Significa transformar a matemática de um obstáculo em uma ferramenta poderosa para alcançar seus objetivos.
Não se esqueça que a consistência é fundamental. Aplique essas técnicas regularmente em sua rotina de estudos. A memorização eficaz é um músculo que se fortalece com o exercício contínuo. Com dedicação e as estratégias certas, aquele "branco" na hora da prova será apenas uma lembrança distante.
Agora é com você! Coloque essas técnicas em prática, conquiste as fórmulas matemáticas e abra as portas para um futuro de sucesso acadêmico e profissional. Boa sorte e bons estudos!