Área do Triângulo
Dominando a Área do Triângulo
Em um universo onde a matemática se entrelaça com o cotidiano, a Área do Triângulo emerge como um conceito fundamental, presente desde os cálculos mais básicos da geometria plana até aplicações complexas em engenharia, arquitetura e computação gráfica. Compreender a Área do Triângulo não é apenas memorizar uma fórmula, mas sim desvendar a lógica por trás da medição de superfícies triangulares, que são, por sua natureza, as formas poligonais mais simples e, paradoxalmente, as mais versáteis. Este artigo visa explorar em profundidade o conceito de Área do Triângulo, apresentando suas diversas abordagens de cálculo, suas interpretações e, acima de tudo, sua relevância prática. Prepare-se para uma jornada didática que transformará sua percepção sobre este pilar da geometria.
Desde os tempos antigos, civilizações como os egípcios e os babilônios já utilizavam princípios rudimentares para calcular a Área do Triângulo em suas construções e demarcações de terras. A necessidade de medir espaços e dividir propriedades impulsionou o desenvolvimento de métodos que, com o tempo, foram refinados e formalizados pelos matemáticos gregos. Euclides, em sua obra
“Os Elementos”, consolidou muitos desses conhecimentos, estabelecendo as bases para a geometria que conhecemos hoje. A Área do Triângulo é, portanto, um conceito com uma rica história, que reflete a evolução do pensamento matemático e sua aplicação na resolução de problemas do mundo real.
Neste artigo, vamos desmistificar a Área do Triângulo, tornando-a acessível a todos, desde estudantes que estão tendo seu primeiro contato com o tema até entusiastas da matemática que desejam aprofundar seus conhecimentos. Abordaremos as fórmulas mais comuns, como a clássica base vezes altura dividido por dois, mas também exploraremos métodos menos convencionais, como a fórmula de Heron e o cálculo da Área do Triângulo utilizando coordenadas cartesianas. Além disso, discutiremos a importância da Área do Triângulo em diversas áreas do conhecimento, demonstrando como um conceito aparentemente simples pode ter um impacto tão significativo. Nosso objetivo é fornecer um guia completo e didático sobre a Área do Triângulo, otimizado para que você encontre facilmente as informações que procura e, mais importante, compreenda verdadeiramente este conceito fundamental.
Conceitos Fundamentais para Entender a Área desta figura
Para compreender plenamente a este conteúdo, é essencial primeiro solidificar alguns conceitos básicos da geometria. Um triângulo é uma das formas mais elementares e, ao mesmo tempo, mais versáteis da geometria. Sua simplicidade esconde uma profundidade matemática que permite sua aplicação em inúmeros contextos. A Área desta figura é, em essência, a medida da superfície bidimensional que ele ocupa. Mas o que define um triângulo e quais são os elementos cruciais para calcular sua área?
O que é um Triângulo?
Um triângulo é um polígono de três lados e três ângulos. É a forma poligonal mais simples, pois não é possível construir um polígono com menos de três lados. A soma dos ângulos internos de qualquer triângulo é sempre 180 graus. Essa propriedade fundamental é a base para muitas outras relações e teoremas na geometria. Os triângulos podem ser classificados de diversas maneiras, tanto em relação aos seus lados quanto aos seus ângulos. Em relação aos lados, temos:
•Triângulo Equilátero: Todos os três lados têm a mesma medida, e consequentemente, todos os três ângulos internos são iguais a 60 graus. Calcular a Área do Triângulo equilátero possui uma fórmula específica que simplifica o processo.
•Triângulo Isósceles: Possui dois lados com a mesma medida e, consequentemente, os ângulos opostos a esses lados também são iguais. A Área do Triângulo isósceles pode ser calculada usando a fórmula geral, mas a simetria pode facilitar a identificação da altura.
•Triângulo Escaleno: Todos os três lados têm medidas diferentes, e todos os três ângulos internos também são diferentes. A Área do Triângulo escaleno geralmente requer a aplicação da fórmula tradicional ou da fórmula de Heron.
Em relação aos ângulos, os triângulos podem ser:
•Triângulo Retângulo: Possui um ângulo interno de 90 graus (ângulo reto). Os lados que formam o ângulo reto são chamados de catetos, e o lado oposto ao ângulo reto é a hipotenusa. A Área do Triângulo retângulo é particularmente fácil de calcular, pois os catetos podem servir como base e altura.
•Triângulo Acutângulo: Todos os três ângulos internos são agudos (menores que 90 graus). A Área do Triângulo acutângulo é calculada como a de qualquer outro triângulo, mas a altura pode cair dentro ou fora do triângulo, dependendo da base escolhida.
•Triângulo Obtusângulo: Possui um ângulo interno obtuso (maior que 90 graus). Assim como no triângulo acutângulo, a altura para a Área do Triângulo obtusângulo pode cair fora da base, exigindo uma projeção da base para encontrar o ponto de intersecção com a altura.
Compreender essas classificações é crucial, pois, embora a fórmula geral para a Área do Triângulo seja aplicável a todos eles, certas propriedades específicas de cada tipo podem simplificar o cálculo ou exigir abordagens ligeiramente diferentes. A Área do do polígono que descrevemos é um conceito unificador, mas sua aplicação prática se beneficia do conhecimento das particularidades de cada forma triangular.
Altura e Base: Pilares do cálculo da área
Os dois elementos mais cruciais para o cálculo da Área do Triângulo pela fórmula mais conhecida são a base e a altura. A base de um triângulo pode ser qualquer um dos seus três lados. A escolha da base é arbitrária, mas a altura correspondente a essa base é única e fundamental. A altura de um triângulo, em relação a uma base específica, é a distância perpendicular do vértice oposto a essa base até a linha que contém a base. É importante notar que a altura nem sempre cai dentro do triângulo, especialmente em triângulos obtusângulos, onde a altura pode cair fora da base, exigindo uma extensão imaginária da base para que a perpendicular possa ser traçada. A Área da figura depende diretamente da correta identificação e medição desses dois elementos.
Visualizar a altura é um passo crítico para calcular a Área da figura que iremos trabalhar hoje. Imagine um triângulo e escolha um de seus lados como base. Agora, imagine uma linha reta que passa por essa base. A altura será a linha perpendicular a essa linha da base que vai até o vértice oposto. Essa linha perpendicular forma um ângulo de 90 graus com a base (ou sua extensão). A Área do Triângulo é, em essência, a metade da área de um paralelogramo (ou retângulo) que teria a mesma base e altura do triângulo. Essa é a intuição por trás da fórmula mais comum para a Área do Triângulo.
Para ilustrar, considere um triângulo ABC. Se escolhermos o lado BC como base, a altura correspondente será o segmento de reta que parte do vértice A e é perpendicular ao lado BC (ou à sua extensão). A Área da figura é então calculada com base nessas duas medidas. A precisão na medição da base e da altura é diretamente proporcional à precisão do cálculo da Área do Triângulo. Em problemas práticos, a identificação correta da altura pode ser o maior desafio, mas uma vez dominada, o cálculo da Área se torna uma tarefa simples e direta.
Métodos para Calcular a Área do Triângulo
Existem diversas maneiras de calcular a Área da nossa figura, cada uma adequada a diferentes contextos e informações disponíveis. A escolha do método depende dos dados que você possui sobre o triângulo. Vamos explorar as principais fórmulas e suas aplicações, garantindo que você tenha um arsenal completo para determinar a Área do Triângulo em qualquer situação.
Fórmula Tradicional: Base x Altura / 2
A fórmula mais conhecida e amplamente utilizada para calcular a Área do Triângulo é a que envolve a base e a altura. Ela é expressa como:
**Área = (base × altura) / 2
Onde:
•base (b): é a medida de um dos lados do triângulo.
•altura (h): é a medida da distância perpendicular do vértice oposto à base até a linha que contém a base.
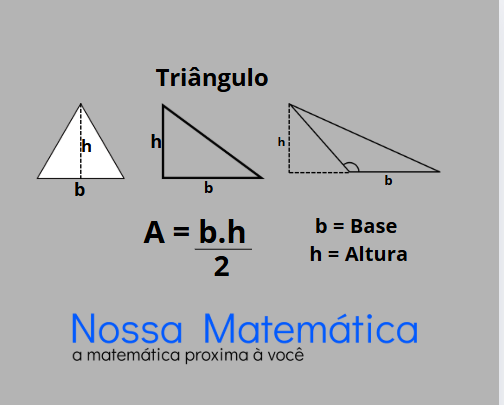
Esta fórmula deriva do fato de que qualquer triângulo pode ser visto como a metade de um paralelogramo (ou retângulo, em casos específicos) com a mesma base e altura. Se você imaginar um triângulo e duplicá-lo, girando uma das cópias e unindo-a à original, você formará um paralelogramo. A área desse paralelogramo é base vezes altura, e como o triângulo é metade dele, sua Área do Triângulo é, portanto, (base × altura) / 2. Esta é a maneira mais intuitiva de entender a Área do Triângulo.*.
Exemplo de Aplicação: Considere um triângulo com uma base de 10 cm e uma altura de 6 cm. Para calcular a Área:
Área = (10 cm × 6 cm) / 2 Área = 60 cm² / 2 Área = 30 cm²
Este método é direto e eficaz, desde que você tenha as medidas da base e da altura correspondente. É a primeira fórmula que se aprende ao estudar a Área do Triângulo e serve como base para a compreensão de outros métodos mais complexos. A simplicidade e a clareza desta fórmula a tornam a pedra angular para o cálculo da Área do Triângulo.
Área do Triângulo com Coordenadas Cartesianas
Quando os vértices de um triângulo são dados em um plano cartesiano, podemos calcular a Área do Triângulo sem a necessidade de determinar a base e a altura diretamente. Este método é particularmente útil em geometria analítica e em aplicações computacionais. Se os vértices do triângulo são A(x₁, y₁), B(x₂, y₂) e C(x₃, y₃), a Área do Triângulo pode ser calculada usando a fórmula do determinante ou a fórmula do cadarço (shoelace formula).
Fórmula do Determinante:
Área = ½ |x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|
Onde o símbolo |…| indica o valor absoluto, pois a área deve ser sempre positiva. Este método é elegante e eficiente para encontrar a Área do Triângulo quando as coordenadas são conhecidas.
Fórmula do Cadarço (Shoelace Formula):
Este método é visualmente mais intuitivo para alguns e envolve listar as coordenadas dos vértices em uma coluna, repetindo a primeira coordenada no final, e então somar os produtos das diagonais. A Área do Triângulo é metade do valor absoluto da diferença entre a soma dos produtos das diagonais para a direita e a soma dos produtos das diagonais para a esquerda.
Área = ½ |(x₁y₂ + x₂y₃ + x₃y₁) – (y₁x₂ + y₂x₃ + y₃x₁)|
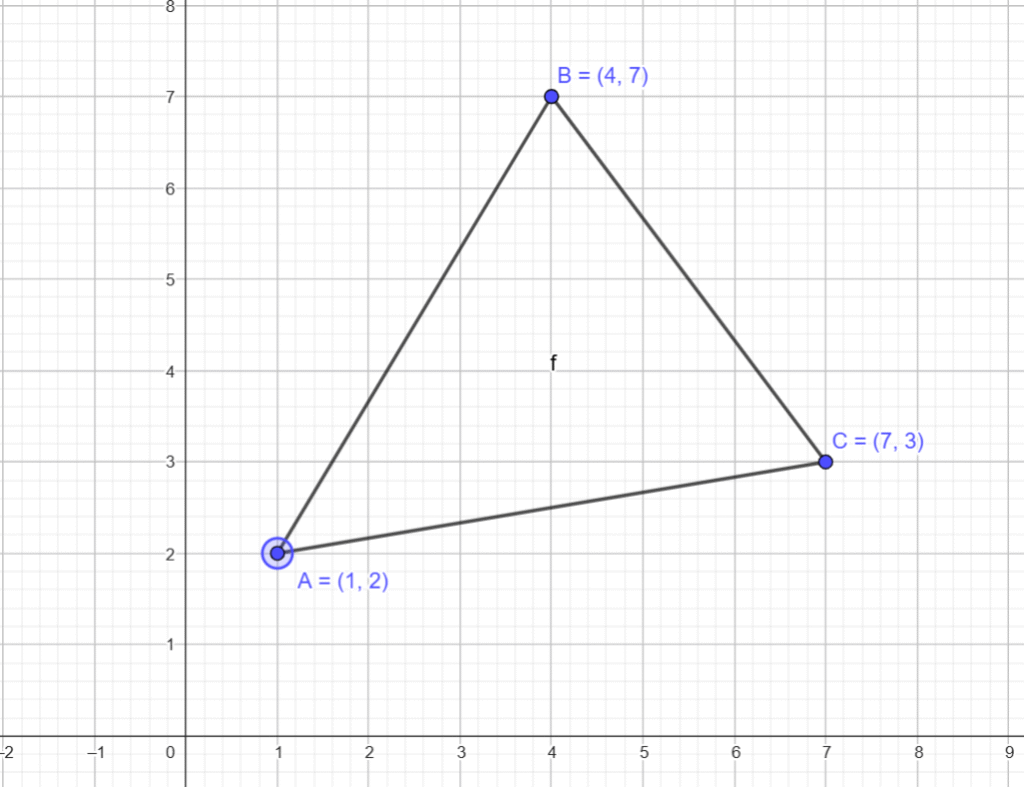
Exemplo de Aplicação: Considere um triângulo com vértices A(1, 2), B(4, 7) e C(7, 3). Para calcular a Área do Triângulo usando a fórmula do cadarço:
x₁ = 1, y₁ = 2 x₂ = 4, y₂ = 7 x₃ = 7, y₃ = 3
Produtos para a direita: (1 × 7) + (4 × 3) + (7 × 2) = 7 + 12 + 14 = 33
Produtos para a esquerda: (2 × 4) + (7 × 7) + (3 × 1) = 8 + 49 + 3 = 60
Área = ½ |33 – 60| Área = ½ |-27| Área = ½ × 27 Área = 13.5 unidades de área
Este método para a Área do Triângulo é extremamente versátil e evita a necessidade de traçar o triângulo ou calcular alturas, sendo ideal para problemas em que as coordenadas dos vértices são fornecidas. É uma ferramenta poderosa para quem trabalha com geometria analítica e computacional, facilitando o cálculo da Área do Triângulo em sistemas de coordenadas.
Área do Triângulo Usando a Fórmula de Heron
A Fórmula de Heron é uma maneira elegante de calcular a Área do Triângulo quando você conhece as medidas de todos os três lados, mas não a altura. Este método é particularmente útil em situações onde a altura é difícil de determinar ou não é fornecida. A fórmula de Heron exige o cálculo do semiperímetro do triângulo primeiro.
O semiperímetro (s) é a metade do perímetro do triângulo. Se os lados do triângulo são a, b e c, então:
s = (a + b + c) / 2
Uma vez que o semiperímetro é calculado, a Área do Triângulo é dada por:
Área = √[s(s – a)(s – b)(s – c)]
Onde √ indica a raiz quadrada. Esta fórmula é uma prova da beleza e interconexão dos conceitos matemáticos, permitindo calcular a Área do Triângulo a partir de informações que, à primeira vista, não parecem diretamente relacionadas à área.
Exemplo de Aplicação: Considere um triângulo com lados a = 3 cm, b = 4 cm e c = 5 cm. Para calcular a Área do Triângulo usando a Fórmula de Heron:
Primeiro, calcule o semiperímetro (s): s = (3 + 4 + 5) / 2 s = 12 / 2 s = 6 cm
Agora, aplique a Fórmula de Heron para a Área do Triângulo: Área = √[6(6 – 3)(6 – 4)(6 – 5)] Área = √[6(3)(2)(1)] Área = √[36] Área = 6 cm²
É interessante notar que este é um triângulo retângulo (3² + 4² = 5²), e sua área também pode ser calculada pela fórmula tradicional (base = 3, altura = 4): (3 × 4) / 2 = 6 cm². A Fórmula de Heron é uma ferramenta poderosa para calcular a Área do Triângulo em qualquer tipo de triângulo, desde que os comprimentos dos lados sejam conhecidos. É uma alternativa valiosa quando a altura não é facilmente acessível, tornando o cálculo da Área do Triângulo mais flexível.
Área em Triângulos Retângulos
Os triângulos retângulos possuem uma característica especial que simplifica enormemente o cálculo da Área: os dois catetos (os lados que formam o ângulo reto) podem ser considerados, respectivamente, como a base e a altura um do outro. Isso elimina a necessidade de traçar uma altura externa ou de realizar cálculos adicionais para encontrá-la. Se os catetos de um triângulo retângulo são ‘a’ e ‘b’, a Área é simplesmente:
Área = (cateto₁ × cateto₂) / 2
Ou, de forma mais genérica:
Área = (produto dos catetos) / 2
Esta é uma aplicação direta da fórmula tradicional da Área do Triângulo, onde a identificação da base e da altura é trivial devido à presença do ângulo reto. A simplicidade deste cálculo torna a Área do Triângulo retângulo um caso especial e frequentemente abordado em problemas de geometria.
Exemplo de Aplicação: Um triângulo retângulo tem catetos medindo 8 cm e 15 cm. Para calcular a Área do Triângulo:
Área = (8 cm × 15 cm) / 2 Área = 120 cm² / 2 Área = 60 cm²
Este método é o mais eficiente para calcular a Área do Triângulo quando se trata de um triângulo retângulo, pois aproveita a própria estrutura da figura. A Área do Triângulo retângulo é um conceito fundamental que serve de base para muitos outros cálculos e teoremas na geometria, incluindo o famoso Teorema de Pitágoras, que relaciona os lados de um triângulo retângulo.
Área em Triângulos Equiláteros
Um triângulo equilátero, por ter todos os lados iguais e todos os ângulos iguais a 60 graus, também possui uma fórmula específica para o cálculo da Área do Triângulo que não exige a altura diretamente, embora ela possa ser facilmente derivada. Se ‘l’ é a medida do lado de um triângulo equilátero, a altura (h) pode ser encontrada por h = (l√3) / 2. Substituindo esta altura na fórmula tradicional da Área do Triângulo (base × altura / 2), onde a base é ‘l’, obtemos a fórmula específica para a Área do Triângulo equilátero:
Área = (l²√3) / 4
Esta fórmula é extremamente conveniente para calcular a Área do Triângulo equilátero, pois você só precisa conhecer a medida de um dos lados. Ela simplifica o processo e é amplamente utilizada em problemas que envolvem essa forma geométrica específica. A Área do Triângulo equilátero é um exemplo de como as propriedades de um tipo específico de triângulo podem levar a fórmulas mais concisas e eficientes.
Exemplo de Aplicação: Calcule a Área do Triângulo equilátero com lado de 6 cm.
Área = (6²√3) / 4 Área = (36√3) / 4 Área = 9√3 cm²
Esta fórmula é um atalho valioso para a Área do Triângulo equilátero, economizando tempo e esforço ao evitar o cálculo intermediário da altura. É um exemplo claro de como a compreensão das propriedades de formas geométricas específicas pode otimizar os cálculos da área.
Aplicações Práticas da Área da figura estudada
A Área da figura que estamos estudando não é apenas um conceito abstrato estudado em salas de aula; ela possui uma vasta gama de aplicações práticas em diversas áreas do conhecimento e do cotidiano. Desde a construção civil até a computação gráfica, a capacidade de calcular a Área é uma habilidade valiosa. Vamos explorar algumas dessas aplicações, destacando a relevância da Área do Triângulo no mundo real.
1. Engenharia e Arquitetura:
Na engenharia civil e na arquitetura, a Área do Triângulo é fundamental para o cálculo de superfícies, volumes e distribuição de cargas. Por exemplo, ao projetar telhados, a Área do polígono de três lados de cada seção é crucial para determinar a quantidade de material necessário (telhas, madeira, etc.) e para garantir a estabilidade da estrutura. Em projetos de paisagismo, o cálculo da área pode ser usada para determinar a quantidade de grama, fertilizante ou outros materiais necessários para cobrir uma determinada área triangular. A precisão no cálculo é vital para a segurança e a economia em qualquer construção.
2. Agrimensura e Topografia:
Agrimensores e topógrafos utilizam a Área do Triângulo para medir e mapear terrenos. Muitas vezes, terrenos irregulares são divididos em uma série de triângulos para facilitar o cálculo de sua área total. A fórmula da Área da figura trabalhada com coordenadas cartesianas é particularmente útil aqui, pois os pontos de referência do terreno podem ser facilmente convertidos em coordenadas. A precisão na medição da Área do Triângulo é essencial para a demarcação de propriedades e para o planejamento urbano.
3. Computação Gráfica e Jogos:
Em computação gráfica, especialmente em modelagem 3D e desenvolvimento de jogos, todos os objetos são construídos a partir de uma malha de triângulos (ou polígonos que podem ser decompostos em triângulos). O cálculo do conteúdo abordado é usado para diversas finalidades, como:
•Renderização: Determinar a visibilidade de superfícies e a forma como a luz interage com elas.
•Detecção de Colisão: Identificar quando dois objetos se chocam, o que muitas vezes envolve verificar a intersecção de triângulos.
•Texturização: Mapear texturas em superfícies 3D, onde a Área do Triângulo pode influenciar a resolução da textura.
A eficiência no cálculo da Área é crucial para o desempenho de jogos e aplicações gráficas, onde milhões de triângulos podem ser processados por segundo.
4. Física e Engenharia Mecânica:
Na física, o cálculo de área pode aparecer em cálculos de vetores, momentos de inércia e centro de massa. Em engenharia mecânica, ao analisar a distribuição de forças em estruturas treliçadas (que são compostas por triângulos), a Área da nossa figura estudada pode ser relevante para determinar a resistência e a estabilidade dos componentes. A compreensão deste conteúdo é, portanto, um pré-requisito para muitos conceitos avançados nessas disciplinas.
Conclusão: Dominando a Área
A jornada através do conceito de Área do Triângulo revela muito mais do que uma simples fórmula matemática. Ela nos mostra a interconexão entre a geometria, a álgebra e a trigonometria, e como um conceito aparentemente básico pode ter ramificações profundas e aplicações práticas em inúmeras disciplinas. Desde a fórmula tradicional que relaciona base e altura, passando pela elegância da fórmula de Heron para triângulos com lados conhecidos, até a precisão do cálculo com coordenadas cartesianas e a versatilidade da abordagem trigonométrica com o seno, cada método oferece uma perspectiva única sobre como quantificar o espaço ocupado por essa forma geométrica fundamental.
Compreender a Área da figura que estudamos é mais do que memorizar equações; é desenvolver uma intuição espacial e uma capacidade de resolução de problemas que são valiosas em qualquer campo. Seja você um estudante buscando excelência acadêmica, um engenheiro projetando estruturas, um desenvolvedor de jogos criando mundos virtuais, ou simplesmente alguém curioso sobre o funcionamento do universo, o domínio da Área do Triângulo é uma habilidade que enriquece sua compreensão do mundo ao seu redor. A Área do Triângulo é um conceito que se aplica em muitos cenários.
