A Área do Retângulo: Desvendando um Conceito Fundamental da Matemática

Introdução: O Retângulo no Nosso Dia a Dia

A matemática, muitas vezes vista como um campo abstrato e complexo, está intrinsecamente ligada ao nosso cotidiano. Desde a construção de edifícios até o design de objetos que usamos diariamente, conceitos matemáticos fundamentais são aplicados de maneiras que nem sempre percebemos. Entre esses conceitos, a área do retângulo se destaca como um dos mais básicos e, ao mesmo tempo, mais versáteis. Compreender a área de um retângulo não é apenas uma habilidade acadêmica; é uma ferramenta prática que nos permite quantificar espaços, planejar projetos e resolver problemas reais.

Imagine que você está reformando sua casa e precisa comprar pisos para um cômodo retangular. Ou talvez você esteja planejando um jardim e queira saber quanto de grama precisará para cobrir uma área específica. Em ambos os cenários, o conhecimento da área do retângulo é indispensável. Ele nos permite calcular a quantidade exata de material necessário, evitando desperdícios e otimizando recursos. Mas o que exatamente é a área e como a calculamos para um retângulo?

Neste artigo abrangente, vamos mergulhar profundamente no conceito de área do retângulo. Começaremos com uma explicação simples e didática, ideal para estudantes e entusiastas da matemática de todas as idades. Em seguida, exploraremos as diferentes formas de interpretar a área de retângulos, mostrando como esse conceito se manifesta em diversas situações. Além disso, abordaremos a importância da otimização para mecanismos de busca (SEO) para que este conteúdo alcance o maior número possível de pessoas, tornando o aprendizado da matemática acessível a todos. Prepare-se para desvendar os segredos da área do retângulo de uma vez por todas!

O Que é Área? Uma Perspectiva Intuitiva

Antes de nos aprofundarmos na área do retângulo, é crucial entender o que o termo "área" realmente significa. De forma simples, a área é a medida da superfície de uma figura bidimensional. Pense em uma folha de papel: a área dessa folha é a quantidade de espaço que ela ocupa em uma superfície plana. É como se estivéssemos "pintando" essa superfície e medindo a quantidade de tinta necessária para cobri-la completamente.

Para tornar esse conceito mais palpável, imagine que você tem um tapete. A área do tapete é o espaço que ele cobre no chão. Se você tiver dois tapetes de tamanhos diferentes, o tapete com maior área cobrirá uma porção maior do chão. A área é sempre expressa em unidades quadradas, como metros quadrados (m²), centímetros quadrados (cm²), quilômetros quadrados (km²), entre outros. Isso ocorre porque estamos medindo um espaço que possui duas dimensões: comprimento e largura.

Considere um quadrado com lados de 1 centímetro. A área desse quadrado é de 1 centímetro quadrado (1 cm²). Este é o bloco fundamental para medir áreas. Quando calculamos a área de qualquer figura, estamos essencialmente descobrindo quantos desses "blocos" de 1 unidade quadrada cabem dentro dela. Essa visualização é particularmente útil para entender a área do retângulo, pois ela se baseia diretamente na ideia de preencher um espaço com esses pequenos quadrados.

A Fórmula da Área do Retângulo: Simplicidade e Eficácia

A fórmula para calcular a área de um retângulo é uma das mais conhecidas e utilizadas na matemática. Ela é notavelmente simples e, por isso, extremamente eficaz. Para encontrar a área (A) de um retângulo, basta multiplicar o comprimento (C) pela largura (L). Em termos matemáticos, a fórmula é expressa como:

A = C × L

Vamos detalhar cada componente dessa fórmula:

•Comprimento (C): Refere-se à dimensão mais longa do retângulo. Pode ser a base, se o retângulo estiver na horizontal, ou a altura, se estiver na vertical. É importante notar que a escolha de qual lado é o "comprimento" e qual é a "largura" é arbitrária, desde que você use as duas dimensões distintas do retângulo.

•Largura (L): Refere-se à dimensão mais curta do retângulo. Assim como o comprimento, pode ser a altura ou a base, dependendo da orientação do retângulo.

•Área (A): O resultado da multiplicação do comprimento pela largura, expresso em unidades quadradas.

Exemplo Prático

1) Para ilustrar, vamos considerar um retângulo com 5 metros de comprimento e 3 metros de largura. Para calcular sua área, aplicamos a fórmula:

A = 5 m × 3 m A = 15 m²

Isso significa que 15 quadrados de 1 metro por 1 metro caberiam perfeitamente dentro desse retângulo. A simplicidade dessa fórmula a torna acessível e fácil de aplicar em uma vasta gama de situações, desde problemas escolares até aplicações profissionais.

2)

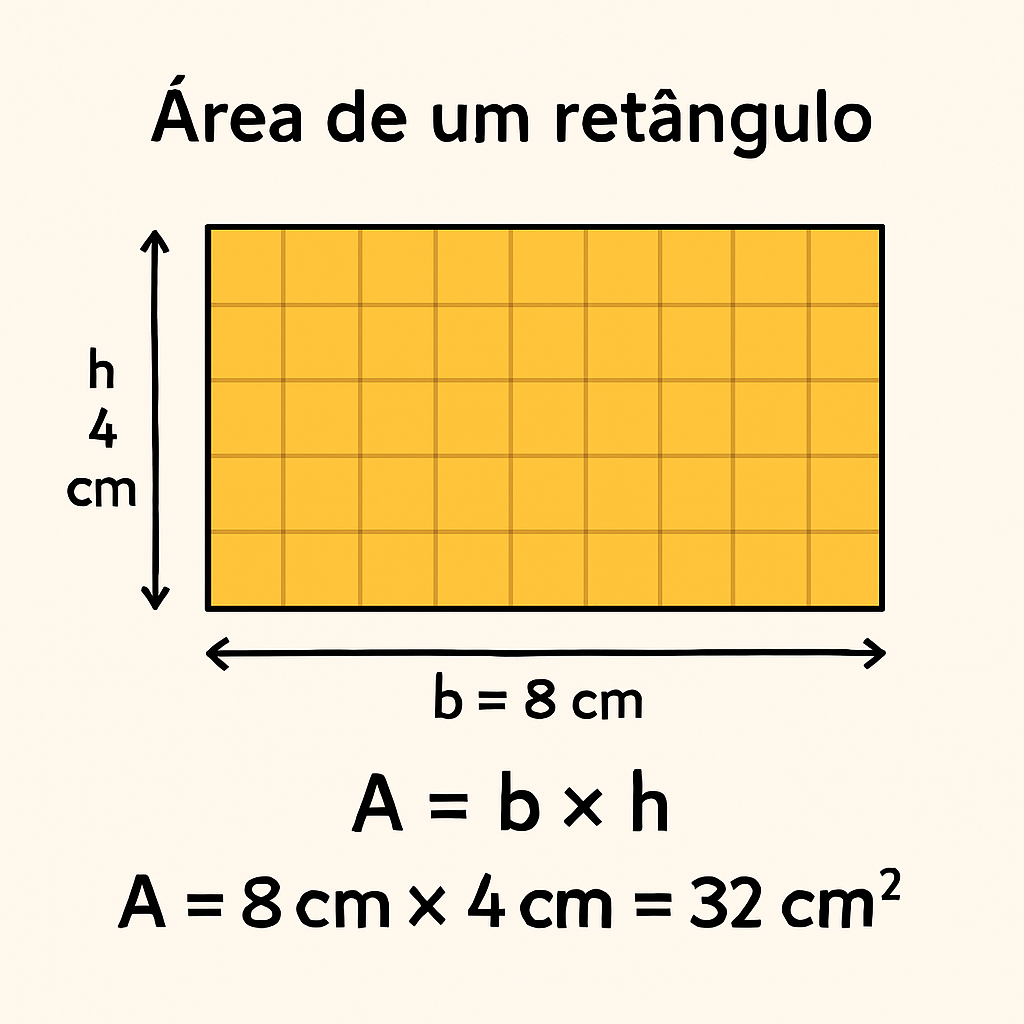
Interpretando a Área do Retângulo: Além da Fórmula

A fórmula A = C × L é a espinha dorsal do cálculo da área do retângulo, mas a verdadeira compreensão do conceito vai além da simples aplicação de uma equação. Existem diferentes maneiras de interpretar e visualizar a área, o que enriquece nosso entendimento e nos permite aplicá-la de forma mais flexível. Vamos explorar algumas dessas interpretações:

1. A Área como Contagem de Unidades Quadradas

Esta é a interpretação mais fundamental e intuitiva. Como mencionado anteriormente, a área de um retângulo pode ser vista como o número de unidades quadradas de um determinado tamanho que cabem dentro de seus limites. Imagine um retângulo desenhado em uma grade quadriculada, onde cada quadrado da grade representa uma unidade de área (por exemplo, 1 cm²).

Se o retângulo tem 4 unidades de comprimento e 3 unidades de largura, você pode literalmente contar os quadrados dentro dele. Você verá que há 4 colunas de 3 quadrados cada, totalizando 12 quadrados. Isso corresponde exatamente ao resultado da fórmula: 4 × 3 = 12 unidades quadradas. Essa interpretação é excelente para iniciantes, pois oferece uma representação visual concreta do que a área realmente significa.

2. A Área como Produto de Duas Dimensões

Esta interpretação é a mais direta e está ligada à própria fórmula. A área é o resultado da multiplicação de duas dimensões perpendiculares entre si: o comprimento e a largura. Essa perspectiva enfatiza que a área é uma medida bidimensional, resultante da combinação de duas medidas lineares. É por isso que a unidade de área é sempre uma unidade de comprimento elevada ao quadrado (m², cm², etc.).

Essa interpretação é crucial para entender por que a ordem da multiplicação não importa (C × L é o mesmo que L × C). Isso reflete a propriedade comutativa da multiplicação e, geometricamente, significa que a orientação do retângulo (deitado ou em pé) não altera a quantidade de superfície que ele ocupa.

3. A Área como Medida de Superfície a Ser Coberta

Em aplicações práticas, a área do retângulo é frequentemente interpretada como a quantidade de superfície que precisa ser coberta por algum material. Por exemplo:

•Pintura: Se você vai pintar uma parede retangular, a área da parede dirá quantos litros de tinta você precisará comprar.

•Piso: Ao colocar piso em um cômodo, a área do cômodo determina quantos metros quadrados de piso são necessários.

•Plantio: Em um canteiro retangular, a área indica o espaço disponível para plantar sementes ou mudas.

Nessa interpretação, a área se torna uma medida de "capacidade de cobertura" ou "espaço disponível". É uma visão muito funcional do conceito, diretamente aplicável a situações do dia a dia e fundamental para o planejamento e a execução de projetos.

4. A Área como Base para Outras Figuras Geométricas

O retângulo é uma figura geométrica fundamental, e sua área serve como base para o cálculo da área de muitas outras formas. Por exemplo:

•Triângulo: A área de um triângulo é metade da área de um retângulo (ou paralelogramo) que o contém. Se você desenhar uma diagonal em um retângulo, você o dividirá em dois triângulos idênticos, cada um com metade da área do retângulo original.

•Paralelogramo: Um paralelogramo pode ser transformado em um retângulo através de um corte e rearranjo. A área de um paralelogramo é, portanto, calculada da mesma forma que a de um retângulo: base vezes altura.

•Trapézio: A área de um trapézio pode ser derivada da área de retângulos e triângulos, ou pela média das bases multiplicada pela altura.

Essa interpretação mostra a importância do retângulo como um bloco construtor na geometria. Ao dominar a área do retângulo, você adquire uma base sólida para entender e calcular a área de formas mais complexas.

5. A Área como Representação de Dados (Gráficos)

Em estatística e visualização de dados, a área de retângulos é frequentemente usada para representar quantidades ou proporções. Histogramas, por exemplo, utilizam retângulos onde a área de cada barra é proporcional à frequência de uma determinada categoria ou intervalo de dados. Isso permite uma representação visual clara da distribuição de dados.

Embora não seja um cálculo direto da área de um objeto físico, essa interpretação demonstra a versatilidade do conceito de área como uma ferramenta para comunicar informações quantitativas de forma eficaz. A área se torna uma metáfora visual para a magnitude de um valor.

Conclusão: A Área do Retângulo como Alicerce do Conhecimento Matemático

A área do retângulo, embora pareça um conceito simples à primeira vista, é um alicerce fundamental no estudo da matemática e suas aplicações. Desde a sua definição intuitiva como a contagem de unidades quadradas até suas interpretações mais avançadas como base para outras figuras geométricas e representação de dados, a compreensão desse conceito abre portas para um vasto universo de conhecimento.

Dominar a fórmula A = C × L é apenas o começo. A verdadeira maestria reside na capacidade de interpretar a área em diferentes contextos, de aplicá-la para resolver problemas práticos e de reconhecer sua presença em diversas áreas do conhecimento. Seja você um estudante buscando solidificar seus fundamentos matemáticos, um profissional que precisa quantificar espaços ou simplesmente alguém curioso sobre o mundo ao seu redor, a área do retângulo é uma ferramenta indispensável.

Ao otimizar este conteúdo para SEO, nosso objetivo é garantir que essa valiosa informação esteja ao alcance de todos. Acreditamos que o conhecimento matemático deve ser acessível, didático e relevante para o dia a dia. Com este artigo, esperamos ter desmistificado a área do retângulo, tornando-a mais compreensível e aplicável para você. Continue explorando o fascinante mundo da matemática com "Nossa Matemática"!

Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=sORRqaz6ml8

Canal: Dicasdemat Sandro Curió

http://www.youtube.com/watch?v=aIKxhaxynJ8

Canal: Gis com Giz Matemática