Área de figuras Planas

3/6/202510 min read

Área de Figuras Planas Desvendada: Guia Completo para o Ensino Fundamental

A matemática está presente em praticamente todos os aspectos do nosso cotidiano, e um dos conceitos mais importantes e práticos é o de área. Quando pensamos em comprar um imóvel, revestir um piso, pintar uma parede ou até mesmo ao escolher um tapete para a sala, estamos lidando com o conceito de área. Mas afinal, o que é área e como calculá-la para diferentes figuras geométricas?

Neste artigo completo, vamos desvendar o conceito de área de figuras planas de forma simples e didática. Você aprenderá a calcular a área de diversas figuras geométricas, desde as mais simples, como quadrados e retângulos, até figuras mais complexas, como trapézios e figuras compostas. Além disso, veremos aplicações práticas e estratégias para resolver problemas envolvendo áreas.

Seja você um estudante do ensino fundamental, um professor buscando material de apoio ou simplesmente alguém interessado em aprimorar seus conhecimentos matemáticos, este guia foi feito para você. Vamos começar nossa jornada pelo mundo das áreas!

O Conceito de Área

A área é uma medida que representa o tamanho de uma superfície ou região plana. Em termos simples, a área nos diz quanto espaço uma figura ocupa em uma superfície. Imagine que você queira cobrir uma mesa com um papel. A quantidade de papel necessária para cobrir completamente a mesa corresponde à área da superfície da mesa.

[IMAGEM: Representação visual do conceito de área com unidades quadradas]

Unidades de Medida de Área

Para medir áreas, utilizamos unidades quadradas. As principais unidades de medida de área no Sistema Internacional (SI) são:

Metro quadrado (m²): usado para medir áreas de cômodos, terrenos pequenos, apartamentos
Centímetro quadrado (cm²): usado para medir áreas de objetos pequenos, como cadernos, livros
Quilômetro quadrado (km²): usado para medir áreas de cidades, estados, países
Hectare (ha): equivalente a 10.000 m², usado principalmente para medir áreas rurais e agrícolas

É importante entender a relação entre essas unidades para fazer conversões quando necessário:

1 m² = 10.000 cm²
1 km² = 1.000.000 m²
1 ha = 10.000 m²

Como Representamos a Área

A área é representada matematicamente pela letra A e é calculada através de fórmulas específicas para cada tipo de figura geométrica. Essas fórmulas relacionam as dimensões da figura (como comprimento, largura, altura, raio) para determinar o espaço ocupado.

Agora que entendemos o conceito básico de área, vamos explorar como calculá-la para diferentes figuras planas.

Área do Quadrado

O quadrado é uma figura geométrica plana com quatro lados iguais e quatro ângulos retos (90°). Por ser uma figura tão regular, o cálculo de sua área é um dos mais simples.

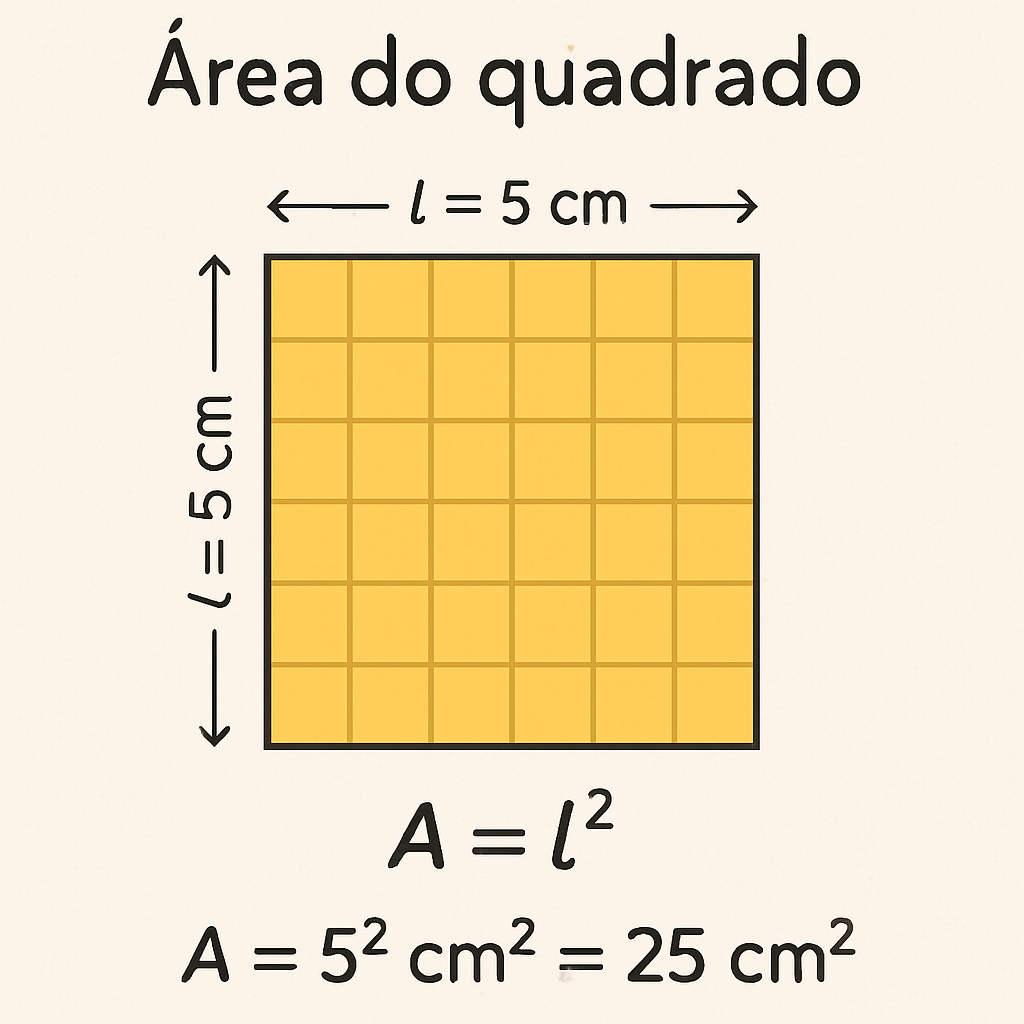
Fórmula da Área do Quadrado

A área de um quadrado é calculada multiplicando-se o comprimento de um lado por ele mesmo, ou seja:

A = l²

Onde:

A é a área do quadrado
l é o comprimento do lado

Exemplo Resolvido

Vamos calcular a área de um quadrado cujo lado mede 5 cm.

Aplicando a fórmula: A = l² A = 5² cm² A = 25 cm²

Portanto, a área desse quadrado é 25 cm².

Aplicações Práticas

O cálculo da área do quadrado é útil em diversas situações do dia a dia, como:

Calcular a quantidade de piso necessária para um cômodo quadrado
Determinar a quantidade de tinta para pintar uma parede quadrada
Calcular a área de um terreno quadrado para construção

Área do Retângulo

O retângulo é uma figura geométrica plana com quatro lados, sendo os lados opostos iguais entre si, e quatro ângulos retos (90°). É uma das figuras mais comuns em nosso cotidiano.

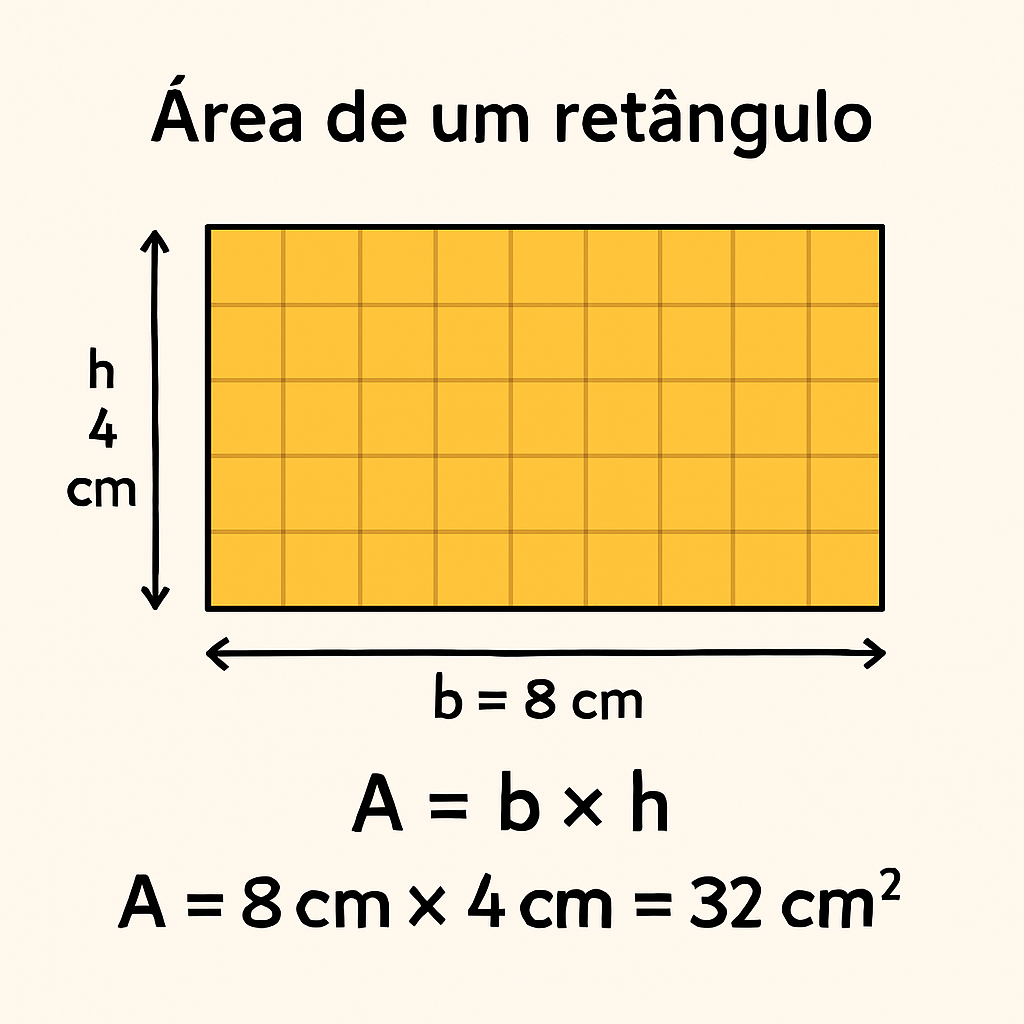
Fórmula da Área do Retângulo

A área de um retângulo é calculada multiplicando-se a base (comprimento) pela altura (largura):

A = b × h

Onde:

A é a área do retângulo
b é a base (comprimento)
h é a altura (largura)

Exemplo Resolvido

Vamos calcular a área de um retângulo com base de 8 cm e altura de 4 cm.

Aplicando a fórmula: A = b × h A = 8 cm × 4 cm A = 32 cm²

Portanto, a área desse retângulo é 32 cm².

Aplicações Práticas

O cálculo da área do retângulo é amplamente utilizado em situações como:

Determinar a quantidade de material para revestir um piso retangular
Calcular a área de um terreno retangular
Determinar a área de uma folha de papel, de uma tela de TV ou de um quadro

Área do Triângulo

O triângulo é uma figura geométrica plana com três lados e três ângulos. Existem diferentes tipos de triângulos (equilátero, isósceles, escaleno, retângulo), mas a fórmula para calcular a área é a mesma para todos.

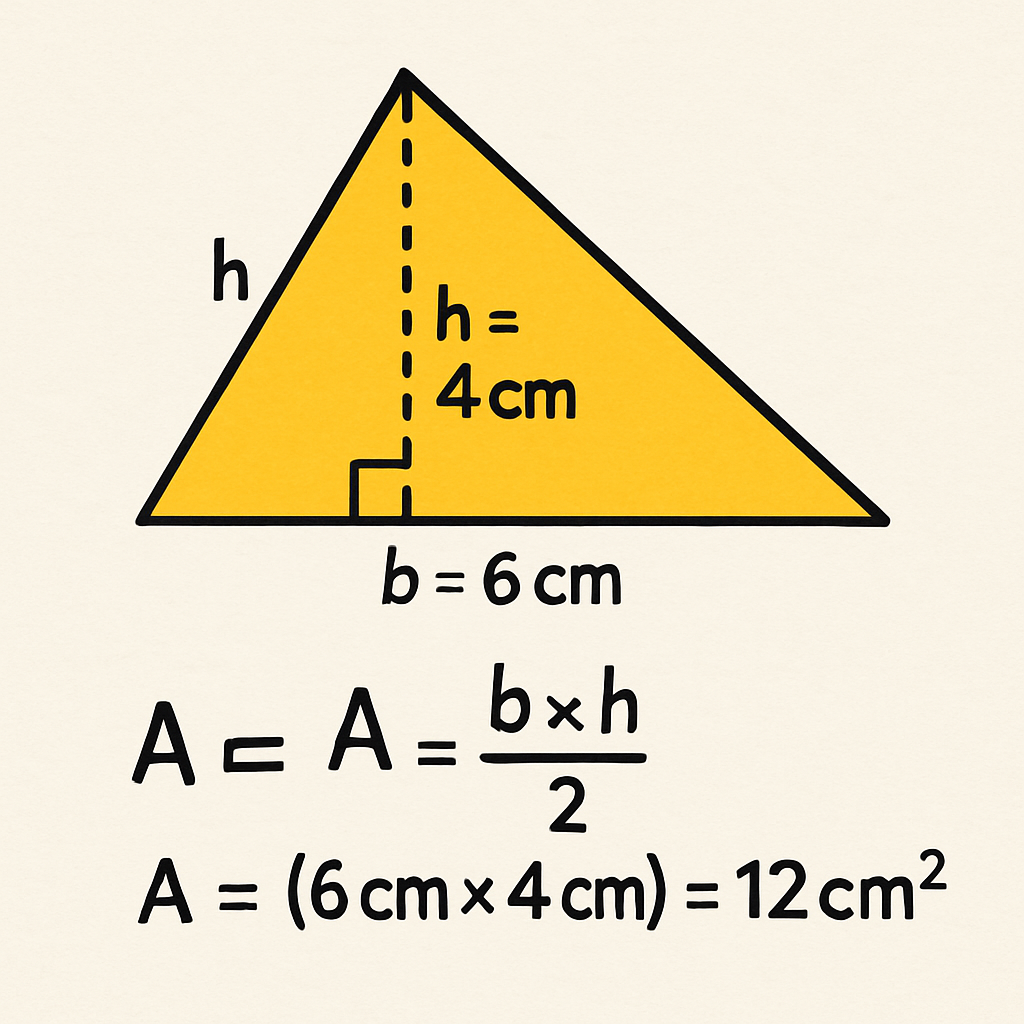
Fórmula da Área do Triângulo

A área de um triângulo é calculada multiplicando-se a base pela altura e dividindo-se o resultado por 2:

A = (b × h) ÷ 2

Onde:

A é a área do triângulo
b é a base
h é a altura (distância perpendicular da base ao vértice oposto)

Exemplo Resolvido

Vamos calcular a área de um triângulo com base de 6 cm e altura de 4 cm.

Aplicando a fórmula: A = (b × h) ÷ 2 A = (6 cm × 4 cm) ÷ 2 A = 24 cm² ÷ 2 A = 12 cm²

Portanto, a área desse triângulo é 12 cm².

Aplicações Práticas

O cálculo da área do triângulo é útil em situações como:

Determinar a área de terrenos triangulares
Calcular a área de telhados com formato triangular
Resolver problemas de engenharia e arquitetura que envolvem estruturas triangulares

Área do Paralelogramo

O paralelogramo é uma figura geométrica plana com quatro lados, sendo os lados opostos paralelos e iguais entre si. Os ângulos opostos também são iguais.

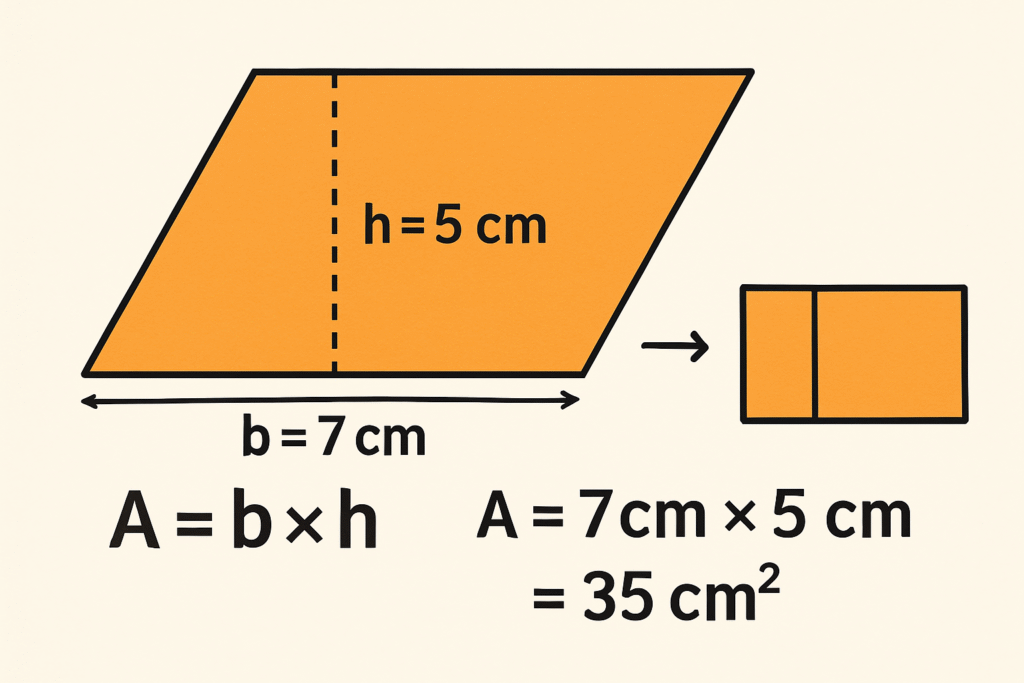
Fórmula da Área do Paralelogramo

A área de um paralelogramo é calculada multiplicando-se a base pela altura:

A = b × h

Onde:

A é a área do paralelogramo
b é a base
h é a altura (distância perpendicular entre os lados paralelos)

Observe que a fórmula é a mesma do retângulo, mas é importante notar que a altura do paralelogramo não é necessariamente igual ao comprimento do lado não paralelo à base.

Exemplo Resolvido

Vamos calcular a área de um paralelogramo com base de 7 cm e altura de 5 cm.

Aplicando a fórmula: A = b × h A = 7 cm × 5 cm A = 35 cm²

Portanto, a área desse paralelogramo é 35 cm².

Relação com o Retângulo

É interessante notar que podemos transformar um paralelogramo em um retângulo de mesma área, recortando um triângulo de um lado e encaixando-o no outro. Isso explica por que a fórmula da área é a mesma para ambas as figuras.

Área do Losango

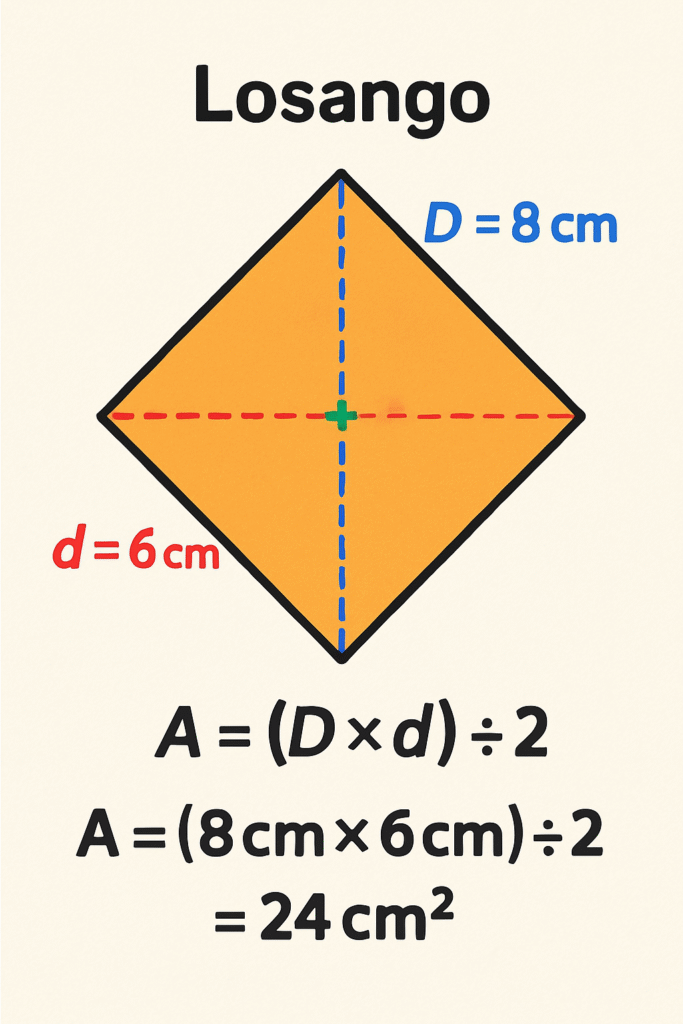
O losango é um paralelogramo especial, onde todos os quatro lados têm o mesmo comprimento. Uma característica importante do losango é que suas diagonais se cruzam no ponto médio e são perpendiculares entre si.

Fórmula da Área do Losango

A área de um losango pode ser calculada de duas maneiras:

Usando a base e a altura (como um paralelogramo): A = b × h
Usando as diagonais (método mais comum): A = (D × d) ÷ 2

Onde:

A é a área do losango
D é a diagonal maior
d é a diagonal menor

Exemplo Resolvido

Vamos calcular a área de um losango com diagonais de 8 cm e 6 cm.

Aplicando a fórmula: A = (D × d) ÷ 2 A = (8 cm × 6 cm) ÷ 2 A = 48 cm² ÷ 2 A = 24 cm²

Portanto, a área desse losango é 24 cm².

Relação com o Quadrado

O losango pode ser visto como um quadrado que foi "empurrado" para o lado. Quando as diagonais de um losango são iguais, ele se torna um quadrado.

Área do Trapézio

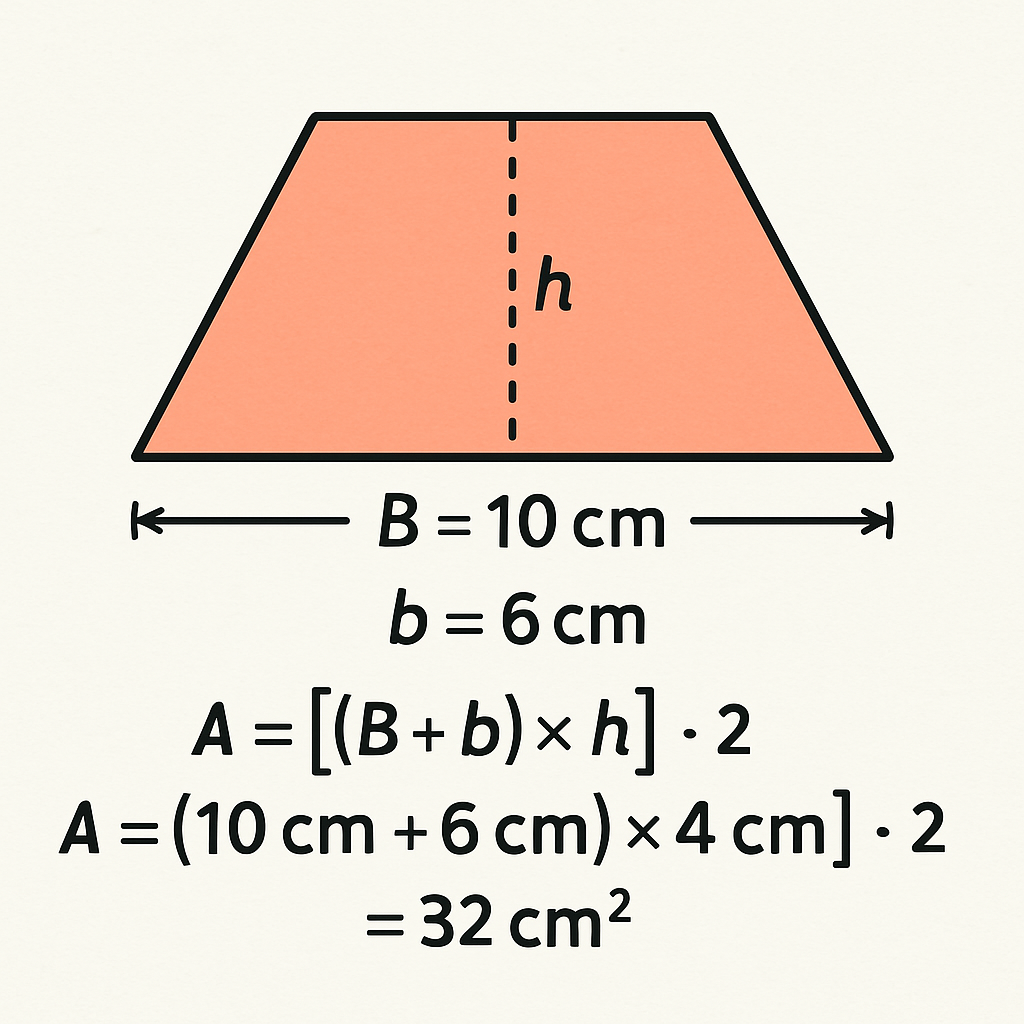
O trapézio é uma figura geométrica plana com quatro lados, sendo dois deles paralelos (chamados de bases) e dois não paralelos.

Fórmula da Área do Trapézio

A área de um trapézio é calculada somando-se as bases, multiplicando pela altura e dividindo por 2:

A = [(B + b) × h] ÷ 2

Onde:

A é a área do trapézio
B é a base maior
b é a base menor
h é a altura (distância perpendicular entre as bases)

Exemplo Resolvido

Vamos calcular a área de um trapézio com base maior de 10 cm, base menor de 6 cm e altura de 4 cm.

Aplicando a fórmula: A = [(B + b) × h] ÷ 2 A = [(10 cm + 6 cm) × 4 cm] ÷ 2 A = [16 cm × 4 cm] ÷ 2 A = 64 cm² ÷ 2 A = 32 cm²

Portanto, a área desse trapézio é 32 cm².

Aplicações Práticas

O cálculo da área do trapézio é útil em situações como:

Determinar a área de terrenos com formato trapezoidal
Calcular a área de telhados ou estruturas com formato de trapézio
Resolver problemas de engenharia que envolvem seções transversais trapezoidais

Área do Círculo

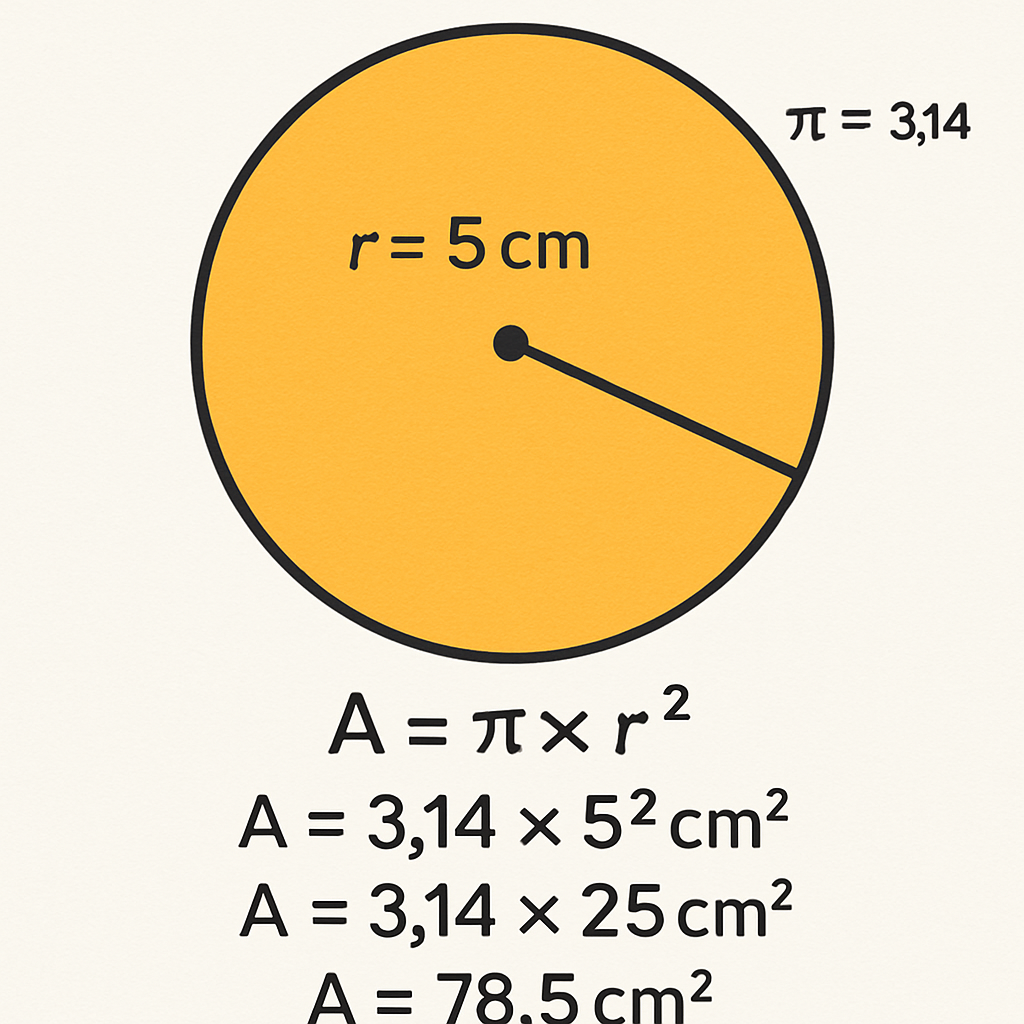
O círculo é uma figura geométrica plana formada por todos os pontos que estão a uma mesma distância (raio) de um ponto central.

Fórmula da Área do Círculo

A área de um círculo é calculada multiplicando-se o quadrado do raio pelo número π (pi):

A = π × r²

Onde:

A é a área do círculo
π (pi) é aproximadamente 3,14
r é o raio do círculo

Exemplo Resolvido

Vamos calcular a área de um círculo com raio de 5 cm.

Aplicando a fórmula: A = π × r² A = 3,14 × 5² cm² A = 3,14 × 25 cm² A = 78,5 cm²

Portanto, a área desse círculo é aproximadamente 78,5 cm².

Aplicações Práticas

O cálculo da área do círculo é útil em situações como:

Determinar a área de pizzas, bolos e outros alimentos circulares
Calcular a área de piscinas circulares
Determinar a quantidade de material necessário para fabricar objetos circulares, como tampas e rodas

Área de Figuras Compostas

Muitas vezes, nos deparamos com figuras que não são simplesmente quadrados, retângulos ou círculos, mas sim combinações dessas figuras básicas. Essas são chamadas de figuras compostas.

Estratégias para Calcular Áreas de Figuras Compostas

Existem duas estratégias principais para calcular a área de figuras compostas:

Método da Adição: Dividimos a figura em partes mais simples, calculamos a área de cada parte e somamos os resultados.
Método da Subtração: Calculamos a área de uma figura maior e subtraímos a área das partes que não fazem parte da figura desejada.

Exemplo Resolvido

Vamos calcular a área de uma figura em forma de "L", composta por dois retângulos: um de 5 cm × 3 cm e outro de 2 cm × 4 cm.

Usando o método da adição: Área do primeiro retângulo = 5 cm × 3 cm = 15 cm² Área do segundo retângulo = 2 cm × 4 cm = 8 cm² Área total = 15 cm² + 8 cm² = 23 cm²

Portanto, a área dessa figura em forma de "L" é 23 cm².

Aplicações Práticas

O cálculo da área de figuras compostas é extremamente útil em situações reais, como:

Determinar a área de casas ou apartamentos com formatos irregulares
Calcular a área de terrenos com formatos não convencionais
Resolver problemas de engenharia e arquitetura que envolvem estruturas complexas

Relação entre Área e Perímetro

Embora área e perímetro sejam conceitos relacionados às figuras geométricas, eles medem aspectos diferentes e não têm uma relação direta de proporcionalidade.

[IMAGEM: Exemplos visuais comparando figuras com mesmo perímetro e áreas diferentes, e vice-versa]

Diferenças e Semelhanças

Perímetro: Mede o contorno ou a fronteira de uma figura (comprimento total)
Área: Mede o espaço interno ou a superfície de uma figura

É importante entender que:

Figuras com o mesmo perímetro podem ter áreas diferentes
Figuras com a mesma área podem ter perímetros diferentes

Exemplo Comparativo

Considere dois retângulos:

Retângulo 1: 10 cm × 2 cm
Retângulo 2: 6 cm × 6 cm

Calculando o perímetro e a área de cada um:

Retângulo 1:

Perímetro = 2 × (10 cm + 2 cm) = 24 cm
Área = 10 cm × 2 cm = 20 cm²

Retângulo 2:

Perímetro = 2 × (6 cm + 6 cm) = 24 cm
Área = 6 cm × 6 cm = 36 cm²

Observe que ambos têm o mesmo perímetro (24 cm), mas áreas diferentes (20 cm² e 36 cm²).

Estratégias para Resolução de Problemas

Resolver problemas envolvendo áreas de figuras planas requer uma abordagem sistemática. Aqui estão algumas estratégias que podem ajudar:

[IMAGEM: Fluxograma para resolução de problemas de área]

Passos para Resolver Problemas de Área

Identificar a figura geométrica: Determine qual figura ou combinação de figuras está envolvida no problema.
Identificar os dados fornecidos: Verifique quais dimensões ou informações são dadas no problema.
Escolher a fórmula adequada: Selecione a fórmula correta para calcular a área da figura identificada.
Substituir os valores e calcular: Aplique os dados na fórmula e realize os cálculos necessários.
Verificar a unidade de medida: Certifique-se de que a resposta está na unidade de medida adequada.
Interpretar o resultado: Analise se o resultado faz sentido no contexto do problema.

Dicas Úteis

Faça um desenho da figura quando o problema não fornecer uma ilustração
Organize os dados antes de aplicar a fórmula
Verifique se é necessário converter unidades de medida
Para figuras compostas, identifique as figuras básicas que a compõem
Sempre verifique se a resposta é coerente com o contexto do problema

Conclusão

Neste artigo, exploramos o conceito de área de figuras planas, desde as definições básicas até aplicações mais complexas. Aprendemos a calcular a área de diversas figuras geométricas, como quadrados, retângulos, triângulos, paralelogramos, losangos, trapézios e círculos, além de figuras compostas.

Compreender o conceito de área é fundamental não apenas para o sucesso acadêmico na matemática, mas também para diversas aplicações práticas no dia a dia. Desde a compra de um imóvel até a decoração de um ambiente, o conhecimento sobre áreas nos ajuda a tomar decisões mais informadas e precisas.

Lembre-se de que a prática é essencial para dominar esse conceito. Por isso, recomendamos que você resolva as questões de fixação propostas a seguir, aplicando as estratégias e fórmulas que aprendemos.

Algumas video-aulas sobre o assunto:

http://www.youtube.com/watch?v=XPVu6ThD3O0

Canal: Dicasdemat Sandro Curió

http://www.youtube.com/watch?v=7Xb7LxrL1Ws

Canal: Gis com Giz Matemática

Voltar

Exercícios