Adição e subtração de frações
Desvendando a Adição e Subtração de Frações
A adição e subtração de frações são operações fundamentais na matemática que, à primeira vista, podem parecer complexas para muitos estudantes. No entanto, com a abordagem correta e uma compreensão clara dos conceitos envolvidos, é possível desmistificar essas operações e torná-las acessíveis a todos. Este guia completo foi elaborado para fornecer uma explicação detalhada e didática sobre como realizar a adição e subtração de frações, abordando desde os princípios mais básicos até as nuances que podem surgir. Nosso objetivo é transformar a percepção de dificuldade em um processo lógico e intuitivo, permitindo que você domine essas habilidades essenciais para o seu desenvolvimento matemático. Prepare-se para explorar o mundo das frações de uma maneira que você nunca viu antes, com exemplos práticos, interpretações variadas e dicas valiosas para otimizar seu aprendizado.
O que são Frações?
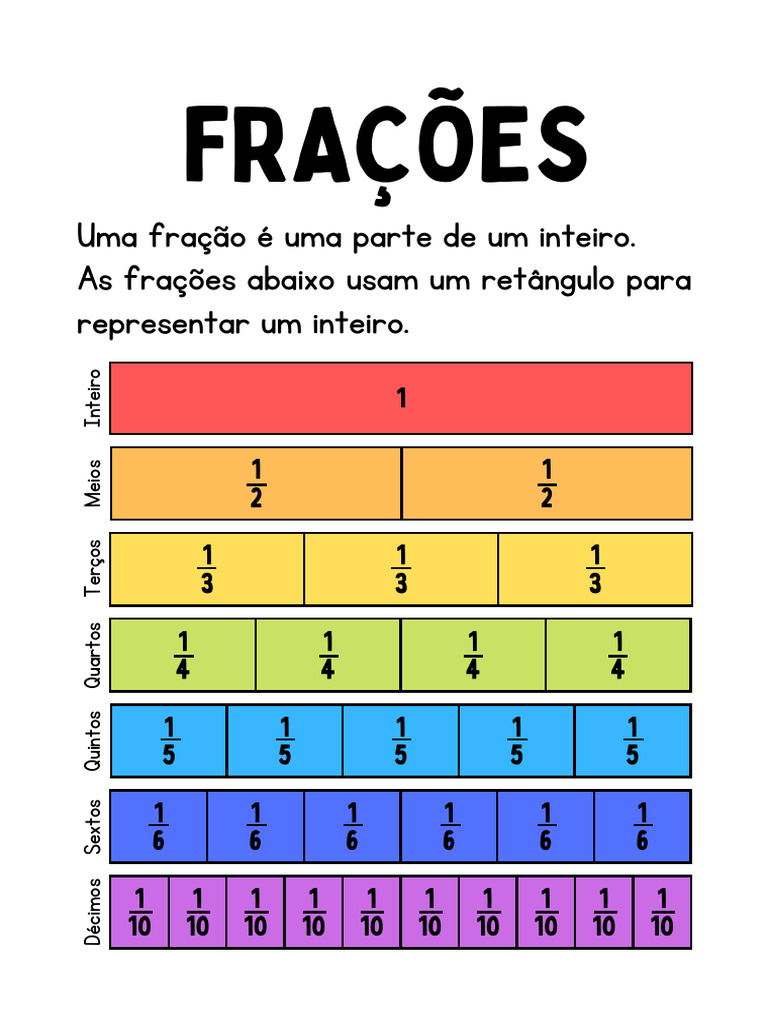
Antes de mergulharmos nas operações de adição e subtração de frações, é crucial relembrar o que são frações. Uma fração representa uma parte de um todo ou uma divisão de um número por outro. Ela é composta por um numerador (o número de cima), que indica quantas partes estamos considerando, e um denominador (o número de baixo), que indica em quantas partes o todo foi dividido. Por exemplo, na fração 1/2, o numerador 1 indica que estamos considerando uma parte, e o denominador 2 indica que o todo foi dividido em duas partes iguais. Compreender essa base é o primeiro passo para dominar a adição e subtração de frações.
Entendendo as Operações com Frações: Conceitos Fundamentais
A adição e subtração de frações seguem princípios lógicos que dependem principalmente dos seus denominadores. A chave para realizar essas operações com sucesso reside em garantir que as frações estejam ‘falando a mesma língua’, ou seja, que representem partes de um todo dividido da mesma forma. Vamos explorar as duas situações principais: quando os denominadores são iguais e quando são diferentes.
Frações com Denominadores Iguais
Quando as frações possuem o mesmo denominador, a adição e subtração de frações tornam-se bastante diretas. Imagine que você tem duas fatias de pizza de um total de oito fatias (2/8) e seu amigo lhe dá mais três fatias da mesma pizza (3/8). Para saber quantas fatias você tem no total, basta somar os numeradores e manter o denominador. O mesmo princípio se aplica à subtração. Se você tinha cinco fatias (5/8) e comeu duas (2/8), você subtrai os numeradores e mantém o denominador. Este é o cenário mais simples para a adição e subtração de frações.
Regra: Para somar ou subtrair frações com denominadores iguais, basta somar ou subtrair os numeradores e manter o denominador comum.
Exemplos:
•Adição: 1/5 + 2/5 = (1+2)/5 = 3/5
•Subtração: 4/7 – 1/7 = (4-1)/7 = 3/7

Esta simplicidade na adição e subtração de frações com denominadores iguais serve como um excelente ponto de partida para construir uma compreensão mais profunda das operações com frações em general. É a base sobre a qual as operações mais complexas são construídas, e dominá-la é essencial antes de avançar para casos com denominadores diferentes. A intuição por trás disso é que, se as partes do todo são do mesmo tamanho (denominador igual), podemos simplesmente contar ou remover as partes (numeradores) sem nos preocuparmos em redimensioná-las. Isso torna a adição e subtração de frações um processo muito mais direto e menos propenso a erros para iniciantes. A visualização de fatias de pizza ou pedaços de bolo é uma ferramenta poderosa para solidificar essa compreensão. Pense em 3/4 de um bolo e adicione 1/4 do mesmo bolo; o resultado é 4/4, ou um bolo inteiro. Da mesma forma, se você tem 5/6 de uma barra de chocolate e come 2/6, você fica com 3/6. A clareza nesse conceito é vital para o avanço no estudo da adição e subtração de frações.
Frações com Denominadores Diferentes
A adição e subtração de frações com denominadores diferentes exigem um passo adicional: encontrar um denominador comum. Isso ocorre porque não podemos somar ou subtrair partes de tamanhos diferentes diretamente. Imagine tentar somar 1/2 de uma pizza com 1/4 de outra pizza; as fatias não são do mesmo tamanho. Para resolver isso, precisamos converter as frações para que tenham o mesmo denominador, sem alterar o valor da fração. O método mais comum para encontrar um denominador comum é através do Mínimo Múltiplo Comum (MMC) dos denominadores.
Passos para Adição e Subtração de Frações com Denominadores Diferentes:
1.Encontre o MMC dos denominadores: O MMC é o menor número que é múltiplo de todos os denominadores envolvidos. Este será o novo denominador comum.
2.Converta as frações: Para cada fração, divida o MMC pelo denominador original e multiplique o resultado pelo numerador. Isso criará uma fração equivalente com o novo denominador.
3.Realize a adição ou subtração: Com os denominadores iguais, proceda como no caso anterior: some ou subtraia os numeradores e mantenha o denominador comum.
4.Simplifique a fração (se necessário): Reduza a fração resultante à sua forma mais simples, dividindo o numerador e o denominador pelo seu Máximo Divisor Comum (MDC).
Exemplo de Adição: 1/2 + 1/3
1.MMC de 2 e 3: O MMC é 6.
2.Converter frações:
•1/2 = (6/2) * 1 / 6 = 3/6
•1/3 = (6/3) * 1 / 6 = 2/6
3.Adicionar: 3/6 + 2/6 = (3+2)/6 = 5/6

Exemplo de Subtração: 3/4 – 1/6
1.MMC de 4 e 6: O MMC é 12.
2.Converter frações:
•3/4 = (12/4) * 3 / 12 = 9/12
•1/6 = (12/6) * 1 / 12 = 2/12
3.Subtrair: 9/12 – 2/12 = (9-2)/12 = 7/12

A compreensão e aplicação do MMC são cruciais para a adição e subtração de frações com denominadores diferentes. Este processo garante que as frações sejam expressas em termos de unidades de tamanho comparável, permitindo que as operações sejam realizadas de forma precisa. A prática constante com diferentes exemplos é a melhor maneira de solidificar essa habilidade, tornando a adição e subtração de frações uma tarefa cada vez mais natural e menos desafiadora. A habilidade de encontrar o MMC e converter frações equivalentes é um pilar para o sucesso em muitas outras áreas da matemática, não apenas na adição e subtração de frações. É um conceito que se estende a problemas de proporção, razão e até mesmo em álgebra, onde a manipulação de expressões fracionárias é comum. Portanto, investir tempo para dominar este aspecto da adição e subtração de frações trará benefícios duradouros para o seu percurso educacional. Lembre-se que a simplificação da fração final é uma etapa importante para apresentar o resultado na sua forma mais concisa e elegante, um hábito que deve ser cultivado ao lidar com a adição e subtração de frações.
Diferentes Formas de Interpretar as Operações com Frações
As operações que estamos estudando podem ser compreendidas de diversas maneiras, o que enriquece o aprendizado e permite que diferentes estilos de pensamento se conectem com o conceito. Além da abordagem puramente algorítmica, que foca nos passos para resolver os problemas, é fundamental explorar as interpretações visuais e conceituais. Essas diferentes perspectivas não só solidificam o entendimento das operações, mas também revelam a beleza e a aplicabilidade das frações em situações do dia a dia. Ao visualizar a adição e subtração de frações de múltiplas formas, o estudante desenvolve uma intuição matemática mais profunda, que vai além da simples memorização de regras. Isso é particularmente útil para aqueles que buscam uma compreensão mais robusta e duradoura, transformando a adição e subtração de frações de um mero cálculo em uma ferramenta poderosa de representação e resolução de problemas.
Frações como Partes de um Todo
A interpretação mais intuitiva da adição e das operações com frações é vê-las como partes de um todo. Essa abordagem é frequentemente utilizada no ensino fundamental e médio, pois permite uma visualização concreta do que as frações representam. Imagine um bolo, uma pizza, uma barra de chocolate ou qualquer objeto que possa ser dividido em partes iguais. Quando falamos em adição e subtração de frações sob essa ótica, estamos literalmente juntando ou retirando pedaços desse todo.
Exemplo Visual de Adição:
Considere que você tem 1/4 de uma pizza e seu amigo lhe dá mais 2/4 da mesma pizza. Para entender a adição e subtração de frações nesse contexto, você pode visualizar a pizza dividida em quatro fatias iguais. Você tem uma fatia, e seu amigo lhe dá mais duas. Juntando as fatias, você terá um total de 3 fatias de 4, ou seja, 3/4 da pizza. A beleza dessa interpretação é que ela torna a operação tangível, facilitando a compreensão do porquê os denominadores precisam ser iguais para que a soma ou subtração seja direta. Se as fatias fossem de tamanhos diferentes (denominadores diferentes), a comparação e a combinação seriam impossíveis sem uma padronização prévia.
Exemplo Visual de Subtração:
Agora, imagine que você tem 5/6 de uma barra de chocolate e decide comer 2/6. Visualmente, a barra de chocolate está dividida em seis pedaços iguais. Você tem cinco desses pedaços. Ao comer dois, você remove duas partes, restando três pedaços de seis, ou 3/6 da barra. Essa representação visual da adição e subtração de frações reforça a ideia de que estamos lidando com quantidades proporcionais de um mesmo objeto. A clareza dessa abordagem é inestimável para construir uma base sólida no entendimento das frações e suas operações. Ela permite que o aluno possa ‘ver’ a matemática acontecendo, o que é muito mais eficaz do que apenas memorizar fórmulas. A adição e subtração de frações se tornam, assim, um conceito palpável e menos abstrato.
Frações na Reta Numérica
Outra forma poderosa de interpretar a adição e subtração de frações é utilizando a reta numérica. Essa abordagem é particularmente útil para desenvolver uma compreensão mais abstrata e para visualizar a magnitude das frações e o resultado das operações. A reta numérica permite que as frações sejam tratadas como pontos em uma linha contínua, onde a distância do zero representa o valor da fração. Isso ajuda a entender que as frações são números como quaisquer outros, e que a adição e subtração de frações são movimentos ao longo dessa linha.
Exemplo na Reta Numérica para Adição:
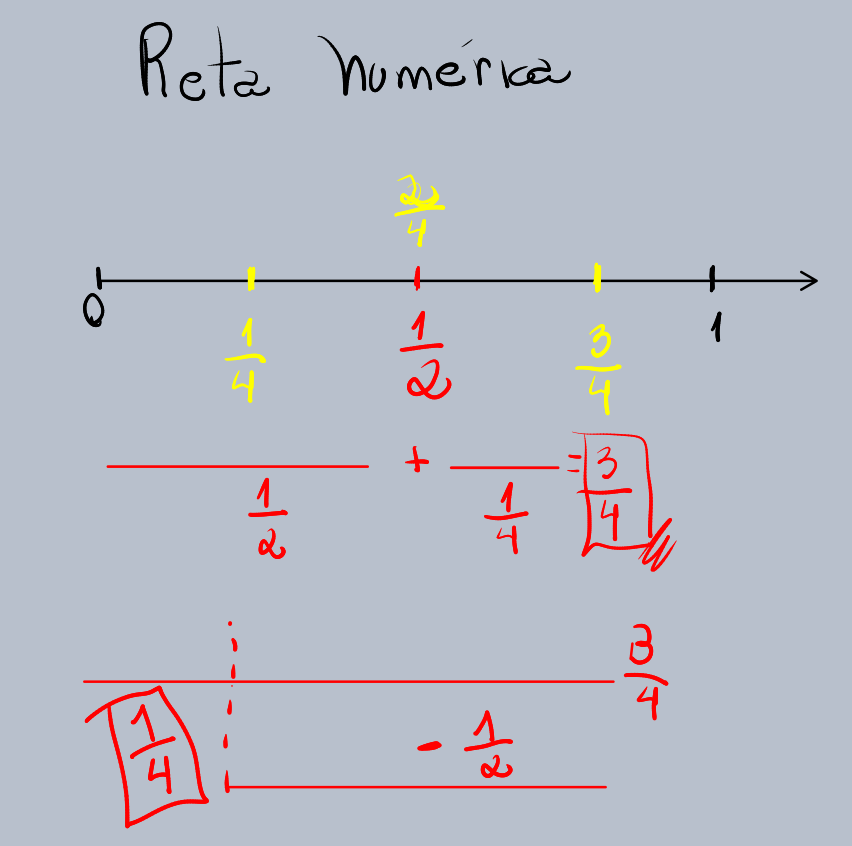
Vamos considerar a adição e subtração de frações com o exemplo 1/2 + 1/4. Primeiro, localize 1/2 na reta numérica. Em seguida, a partir de 1/2, mova-se 1/4 de unidade para a direita (para a adição). Para fazer isso, é necessário que as frações tenham o mesmo denominador. Convertendo 1/2 para 2/4, a operação se torna 2/4 + 1/4. Na reta numérica, você parte do zero, avança 2/4 de unidade, e depois avança mais 1/4 de unidade. O ponto final será 3/4. Essa visualização da adição e subtração de frações na reta numérica ajuda a solidificar a ideia de que estamos combinando ou separando quantidades.
Exemplo na Reta Numérica para Subtração:
Para a adição e subtração de frações com o exemplo 3/4 – 1/2, primeiro localize 3/4 na reta numérica. Em seguida, a partir de 3/4, mova-se 1/2 de unidade para a esquerda (para a subtração). Novamente, convertendo 1/2 para 2/4, a operação se torna 3/4 – 2/4. Na reta numérica, você parte do zero, avança 3/4 de unidade, e depois recua 2/4 de unidade. O ponto final será 1/4. A reta numérica oferece uma representação visual clara da direção e magnitude das operações de adição e subtração de frações. Ela é uma ferramenta valiosa para entender o conceito de valor absoluto e de como as frações se posicionam em relação umas às outras. A adição e subtração de frações na reta numérica é uma excelente forma de complementar a compreensão visual das partes de um todo, oferecendo uma perspectiva mais numérica e posicion
Conclusão: Dominando a Adição e Subtração de Frações
Chegamos ao final deste guia completo sobre adição e subtração de frações. Esperamos que a explicação detalhada, as diferentes formas de interpretação e os exemplos práticos tenham desmistificado essas operações e fornecido as ferramentas necessárias para que você as domine. A matemática, assim como qualquer outra disciplina, exige prática e dedicação. Quanto mais você se familiarizar com os conceitos e aplicar as técnicas aprendidas, mais natural e intuitivo se tornará o processo de realizar a adição e subtração de frações.
Lembre-se que a compreensão das frações vai além da sala de aula; ela é aplicada em diversas situações do cotidiano, desde receitas culinárias até cálculos financeiros. Dominar a adição e subtração de frações é, portanto, uma habilidade valiosa que o acompanhará por toda a vida. Continue praticando, explorando novos desafios e, acima de tudo, divirta-se com a jornada do aprendizado matemático. O “Nossa Matemática” está aqui para apoiar você em cada passo dessa jornada, tornando a adição e subtração de frações e outros tópicos matemáticos acessíveis e compreensíveis para todos. Com este conhecimento, você está bem equipado para enfrentar qualquer problema que envolva a adição e subtração de frações com confiança e precisão. Parabéns pela sua dedicação e continue aprimorando suas habilidades!
