Produtos Notáveis
A Importância dos Produtos Notáveis na Matemática
Os Produtos Notáveis são expressões algébricas que aparecem com frequência em cálculos matemáticos e possuem padrões específicos que permitem a sua resolução de forma mais rápida e eficiente. Ter as noções dos Produtos Notáveis é importante para simplificação, fatoração e na resolução de questões que envolvam expressões numéricas e expressões algébricas. Este guia completo irá desvendar todos os segredos desses padrões algébricos, apresentando-os de forma didática e com exemplos práticos para facilitar o seu aprendizado. Prepare-se para otimizar seus cálculos e aprofundar seus conhecimentos em álgebra com esses conceitos.
O que são Produtos Notáveis?
Em matemática, Produtos Notáveis são resultados de multiplicações de expressões algébricas que seguem um padrão específico. Esses padrões são tão comuns que recebem nomes especiais e fórmulas para facilitar seus cálculos. Em vez de realizar a multiplicação termo a termo, o que pode ser demorado e propenso a erros, podemos aplicar diretamente as fórmulas dos Produtos Notáveis. Isso não pode ajudar a ganhar tempo nas questões. A memorização e a prática dos Produtos Notáveis são cruciais para qualquer estudante de matemática, pois eles são a base para muitos outros tópicos.
Imagine que você precisa calcular (x + y)². Sem saber sobre os Produtos Notáveis, você faria a multiplicação de (x + y) * (x + y), usando o método da distributiva, (ou chuveirinho) e então simplificaria para x² + 2xy + y². Com a fórmula do Quadrado da Soma, um dos Produtos Notáveis mais básicos, você já sabe que o resultado é diretamente x² + 2xy + y². Essa é a beleza e a utilidade dos Produtos Notáveis: eles transformam cálculos extensos em aplicações de fórmulas simples.
Os principais Produtos Notáveis que abordaremos neste artigo são:
•Quadrado da Soma: (a + b)²
•Quadrado da Diferença: (a – b)²
•Produto da Soma pela Diferença: (a + b)(a – b)
•Cubo da Soma: (a + b)³
•Cubo da Diferença: (a – b)³
Cada um desses Produtos Notáveis possui uma fórmula específica e aplicações variadas. Ao longo deste texto, vamos explorar cada um deles em detalhes, com exemplos e explicações didáticas para que você possa dominar completamente os Produtos Notáveis e utilizá-los com confiança em seus estudos e desafios matemáticos. A prática constante é a chave para internalizar esses padrões e torná-los uma ferramenta poderosa em seu arsenal algébrico.
Quadrado da Soma: Um Produto Notável Fundamental
O Quadrado da Soma é um dos Produtos Notáveis mais frequentemente encontrados e é fundamental para a compreensão de conceitos algébricos mais avançados. Ele é representado pela expressão (a + b)², que é o mesmo que: (a + b)*(a + b). Ao invés de realizar a multiplicação distributiva, podemos aplicar a fórmula direta que nos diz que:
(a + b)² = a² + 2ab + b²
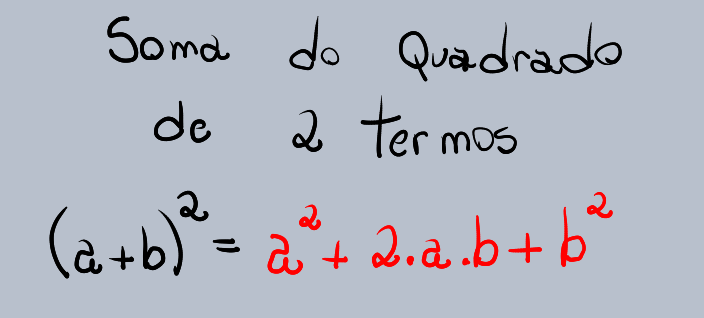
Vamos entender por que ela funciona. Se expandirmos (a + b)² da maneira tradicional, teríamos:
(a + b)² = (a + b) * (a + b)= a² + ab + ba + b² logo:
(a + b)² = a² + 2ab + b²
Como você pode identificar, temos o mesmo resultado da fórmula. Isso demonstra a validade e a conveniência de usar os Produtos Notáveis. A aplicação dessa fórmula economiza tempo e reduz a chance de erros, especialmente em expressões mais complexas. Dominar o Quadrado da Soma é um passo crucial para quem busca fluência em álgebra e para quem deseja aprofundar seus conhecimentos nesses padrões.
Exemplos Práticos do Quadrado da Soma:
1.Exemplo 1: Determine o valor de (y + 9)² Onde, a = y e b = 9.
Aplicando a fórmula: (y + 9)² = y² + 2 * y * 9 + 9²
(y + 8)² = y² + 18y + 81
2.Exemplo 2: Calcule (3z + 7)² Aqui, a = 3z e b = 7.
Aplicando a fórmula: (3z + 7)² = (3z)² + 2 * (3z) * 7 + 7²
(3z + 7)² = 9z² + 42z + 49
3.Exemplo 3: Calcule (a² + b³)² Aqui, a = a² e b = b³.
Aplicando a fórmula: (a² + b³)² = (a²)² + 2 * (a²) * (b³) + (b³)²
(a² + b³)² = a⁴ + 2a²b³ + b⁶
Estes exemplos ilustram a versatilidade do Quadrado da Soma e como ele pode ser aplicado a diferentes tipos de termos. A chave é identificar corretamente o ‘a’ e o ‘b’ na expressão e, em seguida, aplicar a fórmula dos Produtos Notáveis de forma consistente. A prática leva à perfeição, e quanto mais você praticar, mais natural se tornará a aplicação deste e de outros Produtos Notáveis.
Quadrado da Diferença: Outro Produto Notável Essencial
Assim como o Quadrado da Soma, o Quadrado da Diferença é um dos Produtos Notáveis mais importantes e frequentemente utilizados na álgebra. Ele é representado pela expressão (a – b)², que significa (a – b) multiplicado por (a – b). A fórmula para o quadrado da diferença de dois termos é bem parecida com a anterior, com uma crucial, alteração no sinal. A fórmula é:
(a – b)² = a² – 2ab + b²

Podemos entender esta fórmula com a abertura (a – b)² igual fizemos com o quadrado da soma:
(a – b)² = (a – b) * (a – b)= a² – ab – ba + b²
(a – b)² = a² – 2ab + b²
Perceba que o termo do meio, o produto de 2ab, é negativo, o que diferencia esta fórmula da anterior. A capacidade de reconhecer e aplicar rapidamente a fórmula do Quadrado da Diferença é uma habilidade valiosa que acelera a resolução de problemas e minimiza erros. Este Produto Notável é amplamente aplicado em diversas situações, desde a simplificação de expressões até a resolução de equações quadráticas.
Exemplos Práticos do Quadrado da Diferença:
1.Exemplo 1: Calcule (x – 9)² Aqui, a = x e b = 9.
Aplicando a fórmula: (x – 9)² = x² – 2 * x * 9 + 9²
(x – 9)² = x² – 18x + 81
2.Exemplo 2: Calcule (6t – 2z)² Aqui, a = 6t e b = 2z.
Aplicando a fórmula: (6t – 2z)² = (6t)² – 2 * (6t) * (2z) + (2z)²
(6t – 2z)² = 36t² – 24tz + 4z²
3.Exemplo 3: Calcule (y³ – 2)² Aqui, a = y³ e b = 2.
Aplicando a fórmula: (y³ – 2)² = (y³)² – 2 * (y³) * 2 + 2²
(y³ – 2)² = y⁶ – 4y³ + 4
Esses exemplos demonstram a aplicação do Quadrado da Diferença em diferentes contextos. É fundamental nos preocuparmos com os sinais ao aplicar a fórmula. A prática constante com este e outros Produtos Notáveis solidificará sua compreensão e agilidade na resolução de problemas algébricos. A familiaridade com esses padrões é um diferencial em qualquer prova ou desafio matemático.
Produto da Soma pela Diferença: Simplificando Cálculos
O Produto da Soma pela Diferença é um dos Produtos Notáveis mais elegantes e úteis, especialmente para simplificar expressões e fatorar polinômios. Ele é representado pela multiplicação de dois binômios, onde um é a soma de dois termos e o outro é a diferença dos mesmos dois termos: (a + b)(a – b). A fórmula resultante é notavelmente simples e poderosa:
(a + b)(a – b) = a² – b²
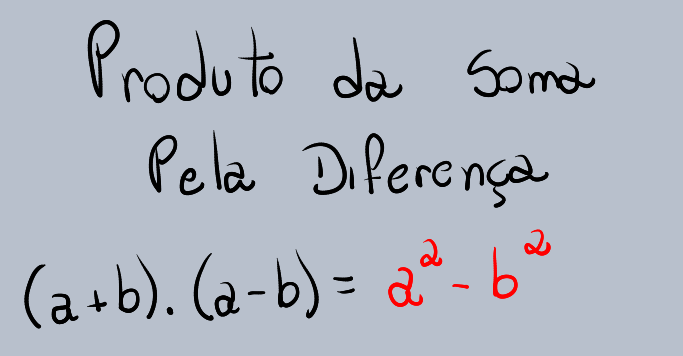
Vamos entender esta fórmula assim como fizemos com a outra, aplicando a distributiva:
(a + b)(a – b) = a² – ab + ba – b²
(a + b)(a – b) = a² – b²
Observe que os termos do meio, -ab e +ba, se cancelam, resultando em uma expressão muito mais concisa. Essa característica torna o Produto da Soma pela Diferença extremamente valioso para simplificar cálculos e para a fatoração de diferenças de quadrados. Reconhecer esse padrão de Produtos Notáveis pode economizar muito tempo e esforço em problemas algébricos. A aplicação deste Produto Notável é vasta, desde a simplificação de frações algébricas até a resolução de equações.
Exemplos Práticos do Produto da Soma pela Diferença:
1.Exemplo 1: Calcule (x + 7)(x – 7) Aqui, a = x e b = 7.
Aplicando a fórmula: (x + 7)(x – 7) = x² – 7²
(x + 7)(x – 7) = x² – 49
2.Exemplo 2: Calcule (2y + 7)(2y – 7) Aqui, a = 2y e b = 7. Aplicando a fórmula: (2y + 7)(2y – 7) = (2y)² – 7² (2y + 7)(2y – 7) = 4y² – 49
3.Exemplo 3: Calcule (5m² + 3n³)(5m² – 3n³) Aqui, a = 5m² e b = 3n³. Aplicando a fórmula: (5m² + 3n³)(5m² – 3n³) = (5m²)² – (3n³)² (5m² + 3n³)(5m² – 3n³) = 25m⁴ – 9n⁶
Com isso podemos ver a praticidade da fórmula. É crucial identificar que os termos são os mesmos em ambos os binômios, apenas com sinais opostos entre eles. Dominar o Produto da Soma pela Diferença é uma habilidade que trará agilidade e precisão aos seus cálculos algébricos.
Cubo da Soma: Expandindo os Conhecimentos
O Cubo da Soma é outro dos Produtos Notáveis importantes, que expande a ideia do quadrado da soma para a terceira potência. Ele é representado pela expressão (a + b)³, que significa (a + b) multiplicado por si mesmo três vezes. A fórmula para o cubo da soma de dois termos é um pouco mais longa, mas segue um padrão lógico e é extremamente útil em diversas aplicações algébricas. A fórmula é:
(a + b)³ = a³ + 3a²b + 3ab² + b³
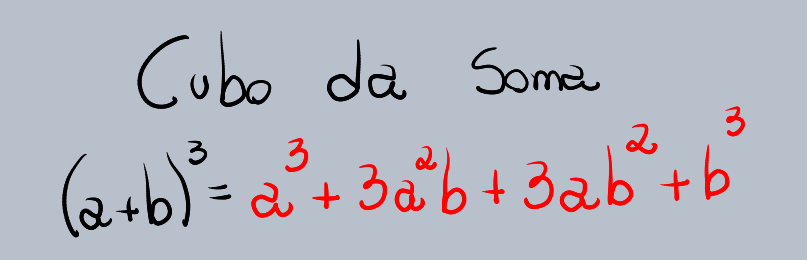
Para derivar essa fórmula, podemos pensar em (a + b)³ como (a + b)² * (a + b).
Já sabemos que (a + b)² = a² + 2ab + b². Agora, multiplicamos esse resultado por (a + b):
(a² + 2ab + b²)(a + b) = (a² * a) + (a² * b) + (2ab * a) + (2ab * b) + (b² * a) + (b² * b)
= a³ + (a²b + 2a²b) + (2ab² + ab²) + b³
= a³ + 3a²b + 3ab² + b³
Como podemos ver, a fórmula do Cubo da Soma é o resultado da expansão cuidadosa. Por mais que parece difícil a primeira vista, pode ser dominada com muitos exercícios de fixação. Este padrão é frequentemente utilizado em problemas de volume, expansão de polinômios e em contextos mais avançados da matemática. Dominar o Cubo da Soma é um sinal de que você está aprofundando seu conhecimento nesses conceitos.
Exemplos Práticos do Cubo da Soma:
1.Exemplo 1: Calcule (x + 3)³ Aqui, a = x e b = 3.
Aplicando a fórmula: (x + 2)³ = (x³) + (3 * x² * 3) + (3 * x * 3²) + (3³)
(x + 2)³ = x³ + 9x² + (3 * x * 9) + 27
(x + 2)³ = x³ + 9x² + 27x + 27
2.Exemplo 2: Calcule (3x + 1)³ Aqui, a = 3x e b = 1.
Aplicando a fórmula: (3x + 1)³ =( 27x³) + (3 * 9x² * 1) + (3 * y * 1²) + (1)³
(y + 3z)³ = y³ + 9y²z + (3 * y * 9z²) + 27z³
(y + 3z)³ = y³ + 9y²z + 27yz² + 27z³
3.Exemplo 3: Calcule (2a + 1)³ Aqui, a = 2a e b = 1.
Aplicando a fórmula: (2a + 1)³ = (2a)³ + 3 * (2a)² * 1 + 3 * (2a) * 1² + 1³
(2a + 1)³ = 8a³ + 12a² + 6a + 1
Estes exemplos demonstram a aplicação do Cubo da Soma em diferentes cenários. É fundamental ser cuidadoso com os coeficientes e as potências ao aplicar a fórmula. A prática constante com este e outros padrões algébricos é a chave para a maestria em álgebra. A compreensão profunda desses conceitos facilita a resolução de problemas complexos e a construção de uma base sólida em matemática.
Cubo da Diferença: o Inverso da Soma
O Cubo da Diferença é o último dos principais Produtos Notáveis que abordaremos em detalhes. Ele é a contraparte do Cubo da Soma e é representado pela expressão (a – b)³, que significa (a – b) multiplicado por si mesmo três vezes. A fórmula para o cubo da diferença de dois termos é similar à do Cubo da Soma, mas com alternância de sinais, o que é crucial para a aplicação correta. A fórmula é:
(a – b)³ = a³ – 3a²b + 3ab² – b³
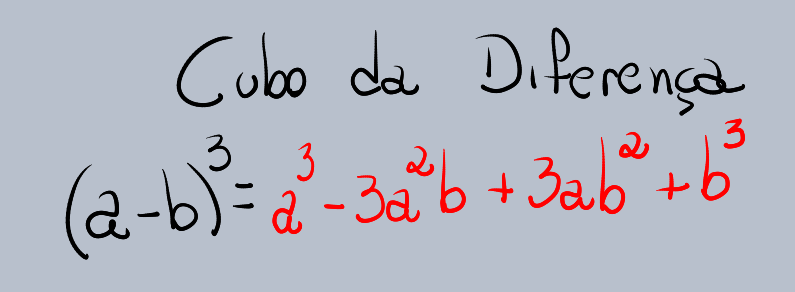
Para entender a derivação dessa fórmula, podemos seguir um raciocínio similar ao do Cubo da Soma, utilizando a expansão de (a – b)² * (a – b).
Já entendemos que (a – b)² = a² – 2ab + b². Agora, multiplicamos esse resultado por (a – b):
(a² – 2ab + b²)(a – b)
= (a² * a) + (a² * (-b)) + ((-2ab) * a) + ((-2ab) * (-b)) + (b² * a) + (b² * (-b))
= a³ – 3a²b + 3ab² – b³
Como você pode observar, a fórmula do Cubo da Diferença apresenta sinais alternados, começando com positivo, depois negativo, positivo e, finalmente, negativo. A atenção aos sinais é fundamental ao aplicar este Produto Notável. Esta é a ultima operação que temos que entender para completar os principais produtos notáveis. Este padrão é valioso para a expansão de expressões e para a fatoração de polinômios de terceiro grau.
Exemplos Práticos do Cubo da Diferença:
1.Exemplo 1: Calcule (x – 5)³ Aqui, a = x e b = 5.
Aplicando a fórmula: (x – 5)³ = x³ – 3 * x² * 5 + 3 * x * 5² – 5³
(x – 5)³= x³ – 15x² + 75x – 125
2.Exemplo 2: Calcule (2y – 5)³ Aqui, a = 2y e b = 5.
Aplicando a fórmula: (2y – 5)³ = (2y)³ – (3 * (2y)² * 5 )+ (3 * (2y) * 5²) – 5³
(2y – 5)³ = 8y³ – 60y² + 150y – 125
3.Exemplo 3: Calcule (m² – n)³ Aqui, a = m² e b = n.
Aplicando a fórmula: (m² – n)³ = (m²)³ – 3 * (m²)² * n + 3 * m² * n² – n³
(m² – n)³ = m⁶ – 3m⁴n + 3m²n² – n³
Estes exemplos reforçam a importância de aplicar a fórmula do Cubo da Diferença com precisão, especialmente em relação aos sinais. A prática contínua com estes e outros padrões é crucial para desenvolver a fluência algébrica e a capacidade de resolver problemas de forma eficiente. A compreensão aprofundada desses conceitos é um pilar para o sucesso em matemática.
Aplicações Práticas dos Produtos Notáveis
Os Produtos Notáveis podem ser usados e aplicados de forma prática em muitas partes da ciência. A capacidade de reconhecer e aplicar esses padrões algébricos pode simplificar significativamente a resolução de problemas complexos, tornando-a mais rápida e eficiente. Vamos explorar algumas das principais aplicações desses conceitos.
Uma das aplicações mais diretas e importantes dos Produtos Notáveis é na fatoração de polinômios. Fatorar um polinômio é nada mais que simbolizar ele como uma multiplicação de fatores mais simples. Podemos entender os Produtos notáveis como formas contrarias as da fatoração
A fatoração é crucial para simplificar expressões algébricas, resolver equações e desigualdades, e para entender o comportamento de funções. Sem o conhecimento desses padrões, a fatoração seria um processo muito mais trabalhoso e menos intuitivo.
Geometria
Os Produtos Notáveis têm uma forte conexão com a geometria, especialmente quando se trata de áreas e volumes. A representação geométrica do Quadrado da Soma, por exemplo, ilustra perfeitamente como a área de um quadrado de lado (a + b) é igual à soma das áreas de um quadrado de lado a, um quadrado de lado b, e dois retângulos de lados a e b. Essa visualização ajuda a entender a lógica por trás das fórmulas e a aplicá-las em problemas de geometria. O Cubo da Soma e o Cubo da Diferença também podem ser visualizados em termos de volumes, o que reforça a compreensão desses Produtos Notáveis.
Conclusão: A Importância Desse Conhecimento Na Matemática
Ao longo deste guia, exploramos em profundidade os principais Produtos Notáveis: o Quadrado da Soma, o Quadrado da Diferença, o Produto da Soma pela Diferença, o Cubo da Soma e o Cubo da Diferença. Vimos que cada um desses Produtos Notáveis possui uma fórmula específica que permite simplificar e agilizar cálculos algébricos que, de outra forma, seriam mais trabalhosos e propensos a erros. A compreensão e a memorização dessas fórmulas são, sem dúvida, um pilar fundamental para o desenvolvimento da fluência em álgebra.
Algumas video-aulas sobre o assunto:
http://www.youtube.com/watch?v=UECy1XbL6w8
Canal: Dicasdemat Sandro Curió
http://www.youtube.com/watch?v=C_dLST3fa6s
Canal: Gis com Giz Matemática
