Adição e Subtração
Adição e Subtração: Os Pilares Fundamentais da Matemática para o Nosso Dia a Dia
Bem-vindo ao Nossa Matemática, o seu portal completo para desvendar os segredos dos números e tornar o aprendizado da matemática uma jornada fascinante e acessível. Neste artigo vamos estudar dois dos conceitos fundamentais e que permeiam por toda a matemática: a adição e a subtração. Por mais que pareçam fáceis à primeira vista, essas operações são o alicerce para cálculos mais complexos e vão estar presentes em todas as situações da nossa vida, desde o troco na mercearia até a gestão de investimentos.
Neste artigo feito pelo Nossa Matemática, você verá uma explicação detalhada e didática sobre o que são a adição e a subtração, como elas aparecem no nosso dia a dia, como executar as operações e por que da sua importância. Abordaremos suas diferentes interpretações, suas propriedades essenciais e como aplicá-las em diversas situações práticas. Nosso objetivo é não apenas ensinar a somar e a diminuir, mas também a compreender a lógica por trás dessas operações, tornando-o um pensador matemático mais confiante e eficiente. Prepare-se para desmistificar a adição e a subtração e descobrir como elas podem simplificar e enriquecer sua vida!
O Que é Adição? Uma Explicação Simples e Didática
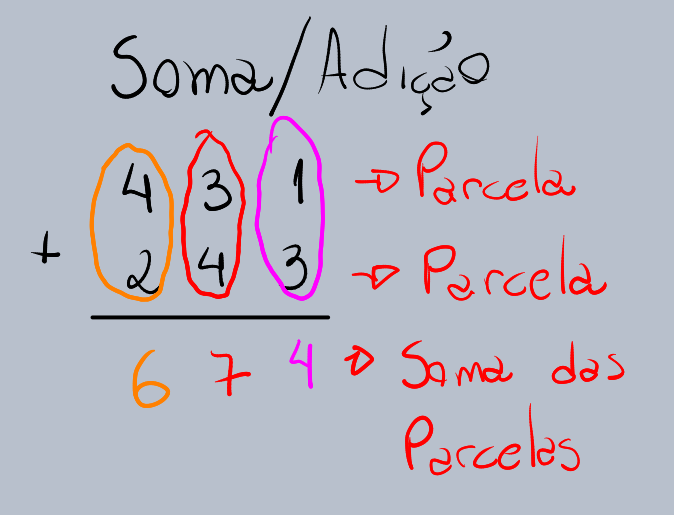
A adição é a operação matemática que nos permite somar parcelas. Em sua essência, é o ato de combinar dois ou mais números para obter um total. O resultado da adição de duas parcelas é chamado de soma ou total. Os números que estão sendo adicionados são conhecidos como parcelas.
Imagine que você tem 3 laranjas em uma cesta e sua amiga lhe dá mais 2 laranjas. Quantas laranjas você tem agora? Para descobrir, você realiza uma adição: 3 laranjas + 2 laranjas = 5 laranjas. Aqui, temos a parcela 3 e adicionamos 2, e 5 é o resultado ou total.
O símbolo que usamos para representar a adição é o sinal de mais (+). Quando vemos esse sinal entre dois números, sabemos que devemos combiná-los. Por exemplo, “2 + 3” significa “dois mais três”, e o resultado é 5.
A Importância da Adição no Cotidiano
A adição não é apenas um conceito abstrato ensinado na escola; ela é uma ferramenta prática que usamos constantemente. Pense em:
•Compras: Calcular o custo total de vários itens no supermercado.
•Tempo: Somar minutos ou horas para planejar um evento ou viagem.
•Finanças: Controlar gastos, somar receitas e gerenciar orçamentos.
•Culinária: Ajustar receitas, somando ingredientes.
•Jogos: Contar pontos, somar dados ou cartas.
Dominar a adição é o primeiro passo para desenvolver uma forte base em matemática e para resolver problemas do dia a dia com facilidade e precisão. É a habilidade que nos permite quantificar, comparar e planejar, tornando-se um pilar fundamental para a nossa vida pessoal e profissional.
O Que é Subtração? Uma Explicação Simples e Didática
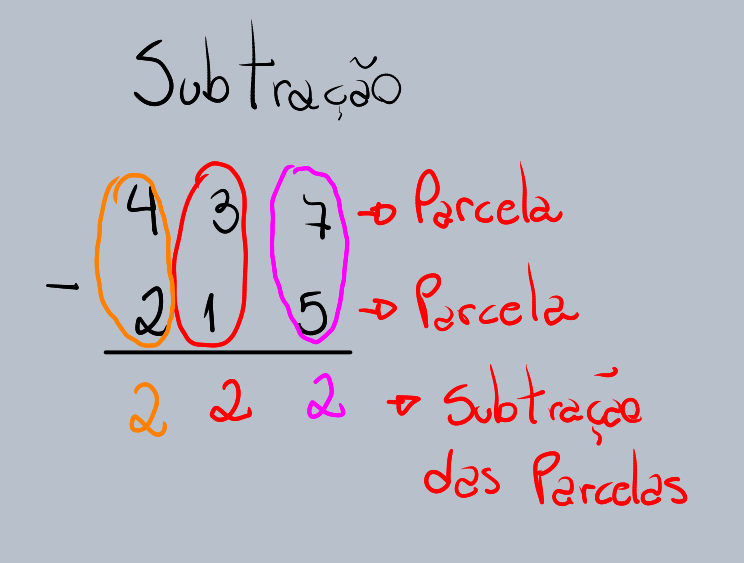
A subtração é a operação matemática que nos permite retirar uma quantidade de outra, comparar quantidades para encontrar a diferença, ou descobrir quanto falta para atingir um valor. O resultado dessa operação é conhecida como de diferença ou sobra. Os números envolvidos na subtração são o minuendo (o número do qual se subtrai) e o subtraendo (o número a ser subtraído).
Imagine que você tem 5 biscoitos e come 2. Quantos biscoitos restam? Para descobrir, você realiza uma subtração: 5 biscoitos – 2 biscoitos = 3 biscoitos. Aqui, 5 é o minuendo, 2 é o subtraendo, e 3 é a diferença ou resto.
O símbolo reconhecido para representar a subtração é o sinal de menos (-). Quando vemos esse sinal entre dois números, sabemos que devemos diminuir o segundo do primeiro. Por exemplo, “7 – 5” significa “sete menos cinco”, e o resultado é 2.
A Importância da Subtração no Cotidiano
A subtração, assim como a adição, é uma habilidade matemática essencial para o dia a dia. Ela nos permite:
•Saber o troco: Saber qual valor deve receber de volta depois uma compra.
•Medir diferenças: Comparar alturas, pesos, idades ou distâncias.
•Controlar estoque: Saber quantos itens restam após vendas ou uso.
•Planejar recursos: Determinar quanto de um recurso (tempo, dinheiro, material) ainda está disponível.
•Resolver problemas: Encontrar a quantidade que falta para completar algo.
Dominar a subtração é tão importante quanto dominar a adição, pois juntas elas formam a base para a compreensão de conceitos matemáticos mais avançados e para a resolução de uma vasta gama de problemas práticos.
Diferentes Formas de Interpretar as operações: Além do “Juntar” e “Retirar”
Embora as ideias de “juntar” para adição e “retirar” para subtração sejam as mais comuns, essas operações podem ser interpretadas de várias maneiras, dependendo do contexto do problema. Compreender essas diferentes perspectivas aprofunda nosso entendimento e nos ajuda a aplicar a adição e a subtração de forma mais eficaz em diversas situações.
Interpretações da Adição:
1. Juntar Quantidades (Combinação)
Esta é a interpretação mais intuitiva e frequentemente a primeira a ser ensinada. Envolve a combinação de dois ou mais grupos distintos para formar um único grupo maior. juntando os grupos.
Exemplo: Você tem 4 lápis azuis e 3 lápis vermelhos. Ao juntar todos os lápis, você tem 4 + 3 = 7 lápis no total.
2. Acrescentar Quantidades (Aumento)
Nesta interpretação, uma quantidade é adicionada a uma quantidade já existente, resultando em um aumento do valor inicial. O foco está na mudança ou no crescimento de uma quantidade.
Exemplo: Você tinha 4 laranjas e ganhou mais 4 laranjas. Agora você tem 4 + 4 = 8 laranjas.
3. Comparação (Diferença para o Total)
Embora a adição seja sobre somar, ela também pode ser usada em problemas de comparação onde se busca o total a partir de uma diferença. Por exemplo, se você sabe que uma quantidade é X a mais que outra, a adição pode ajudar a encontrar a segunda quantidade.
Exemplo: João tem 6 bolinhas de gude. Maria tem 3 bolinhas de gude a mais que João. Quantas bolinhas Maria tem? Aqui, você acrescenta a diferença à quantidade de João: 6 + 3 = 9 bolinhas.
4. Deslocamento na Reta Numérica (Adição)
A adição pode ser interpretada como um movimento na direção dos números positivos na reta numérica. Começamos em um número (a primeira parcela) e nos movemos para a direita o número de unidades da segunda parcela. O ponto final é a soma.
Exemplo: Para calcular 3 + 4:
1.Comece no número 3 na reta numérica.
2.Mova 4 unidades para a direita.
3.Você chegará ao número 7. Portanto, 3 + 4 = 7.
Interpretações da Subtração:
1. Retirar Quantidades (Remoção)
Esta é a interpretação mais comum da subtração. Envolve a remoção de uma parte de um todo, e o resultado é o que resta.
Exemplo: Você tinha 8 balões e 3 estouraram. Quantos balões restam? 8 – 3 = 5 balões.
2. Comparar Quantidades (Diferença)
Nesta interpretação, a subtração é usada para encontrar a diferença entre duas quantidades. Comparamos os valores para descobrir a diferença entre eles.
Exemplo: João tem 10 figurinhas e Pedro tem 7 figurinhas. Quantas figurinhas João tem a mais que Pedro? 10 – 7 = 3 figurinhas.
3. Completar Quantidades (Quanto Falta?)
Esta interpretação envolve descobrir quanto precisa ser adicionado a uma quantidade menor para atingir uma quantidade maior. Normalmente se pergunta “quanto falta para algo chegar em outro algo…” ou “quanto precisa para algo chegar a outro algo…”.
Exemplo: Você tem R$12,00 e quer comprar um livro que custa R$18,00. Quanto dinheiro falta? R$18,00−R$12,00 = R$ 6,00.
4. Deslocamento na Reta Numérica (Subtração)
A subtração pode ser interpretada como andar para a esquerda(direção dos números negativos) na reta numérica. Começamos em um número (o minuendo) e nos movemos para a esquerda o valor que queremos subtrair (subtraendo). O ponto final é o resultado da subtração.
Exemplo: Para calcular 7 – 3:
1.Comece no número 7 na reta numérica.
2.Mova 3 unidades para a esquerda.
3.Você chegará ao número 4. Portanto, 7 – 3 = 4.
Compreender essas diferentes interpretações da adição e da subtração enriquece sua capacidade de modelar e resolver problemas matemáticos do mundo real. Ambas as operações não são conceitos estáticos, mas ferramentas flexíveis que se adaptam a diversas situações.
Propriedades das operações: Simplificando os cálculos
Assim como outras operações matemáticas, a adição e a subtração possuem propriedades que as tornam mais previsíveis e, em muitos casos, simplificam os cálculos. Compreender essas propriedades é essencial para desenvolver fluência e eficiência na resolução de problemas.
Propriedades da Adição:
1. Propriedade Comutativa
Na adição a ordem dos valores não altera o resultado final. Em outras palavras, você pode adicionar números em qualquer ordem e o resultado será o mesmo.
Exemplo:
•2 + 3 = 5
•3 + 2 = 5
Matematicamente, para quaisquer números ‘a’ e ‘b’:
a + b = b + a
Esta propriedade é extremamente útil, pois nos permite reorganizar os números em uma adição para facilitar o cálculo mental ou para agrupar termos semelhantes em expressões mais complexas.
2. Propriedade Associativa
A propriedade associativa da adição estabelece que, de qualquer forma que somarmos três ou mais valores, a maneira como agrupamos essas parcelas não altera o resultado. Os parênteses servem para mostrar a ordem em que as operações devem ser feitas.
Exemplo:
•(7 + 4) + 3 = 11 + 3 = 14
•7 + (4 + 3) = 7 + 7 = 14
Essa propriedade nos dá flexibilidade para agrupar números de forma conveniente, o que é particularmente útil em somas com muitas parcelas. Por exemplo, se você precisa somar 15 + 7 + 3, pode ser mais fácil somar 7 + 3 primeiro (que dá 10) e depois 15 + 10 = 25.
3. Elemento Neutro da Adição
O elemento neutro da adição é o número que, quando adicionado a qualquer outro número, não altera esse número. Na adição, o elemento neutro é o zero (0).
Exemplo:
•5 + 0 = 5
•0 + 12 = 12
Matematicamente, para qualquer número ‘a’:
a + 0 = a 0 + a = a
O zero é fundamental para representar a ausência de quantidade e desempenha um papel crucial em diversas áreas da matemática.
4. Propriedade do Fechamento (Adição)
A propriedade do fechamento, é importante para entender a relação dos conjuntos numéricos com as operações. Ela afirma que, ao adicionar dois números de um determinado conjunto numérico, o resultado também pertencerá a esse mesmo conjunto.
Exemplo:
•Se você soma dois números naturais (ex: 3 + 5 = 8), o resultado (8) também é um número natural.
•Se você soma dois números inteiros (ex: -2 + 7 = 5), o resultado (5) também é um número inteiro.
Propriedades da Subtração:
É importante notar que a subtração não possui as mesmas propriedades da adição. Ela não é comutativa e não é associativa.
Não Comutativa:
A ordem dos fatores na subtração altera o resultado final.
Exemplo:
•5 – 3 = 2
•3 – 5 = -2 (resultados diferentes)
Não Associativa:
A forma como agrupamos os números na subtração altera o resultado.
Exemplo:
•(10 – 4) – 2 = 6 – 2 = 4
•10 – (4 – 2) = 10 – 2 = 8 (resultados diferentes)
Elemento Neutro da Subtração (à direita):
O zero é o elemento neutro quando esta a direita da subtração, porém a esquerda ele altera o resultado,
Exemplo:
•5 – 0 = 5
•0 – 5 = -5 (resultado diferente)
Propriedade do Fechamento (Subtração)
A subtração é fechada para alguns conjuntos numéricos, como os números inteiros, mas não para outros, como os números naturais (por exemplo, 3 – 5 não é um número natural).
Compreender e aplicar essas propriedades não só facilita a realização de cálculos, mas também aprofunda a compreensão sobre a natureza dos números e das operações matemáticas. Elas são o alicerce para o desenvolvimento de recursos de cálculo mental e nos ajuda na resolução de problemas mais complicados.
Estratégias de Cálculo Mental para soma e subtração: Agilidade e Precisão
O cálculo mental é uma habilidade valiosa que nos permite realizar operações matemáticas rapidamente, sem a necessidade de lápis, papel ou calculadora. Para a adição e a subtração, existem diversas estratégias que podem ser empregadas para aumentar a agilidade e a precisão.
Estratégias para Adição:
1. Decomposição de Números
Esta estratégia consiste em quebrar um dos valores em partes que sejam ou uma dezena, centena ou milhar exata para facilitar a adição.
Exemplo: Calcular 47 + 25
•Decomponha 25 em 20 + 5.
•Some 47 + 20 = 67.
•Some o restante: 67 + 5 = 72.
Ou, decomponha 47 em 40 + 7:
•Some 40 + 25 = 65.
•Some o restante: 65 + 7 = 72.
2. Arredondamento e Compensação
Esta técnica consiste em arredondar um dos números para a dezena, centena ou milhar mais próxima, realizar a adição e depois compensar a diferença.
Exemplo: Calcular 38 + 53
•Arredonde 38 para 40 (adicionou 2).
•Some 40 + 53 = 93.
•Compense subtraindo o 2 que foi adicionado: 93 – 2 = 91.
3. Contagem Progressiva
Útil para números menores, esta estratégia consiste em contar do valor maior e ir subindo com o valor menor
Exemplo: Calcular 12 + 7
•Comece com 12.
•Suba 7 unidades : 13, 14, 15, 16, 17, 18, 19.
•Resultado: 19.
4. Agrupamento para Dezenas/Centenas
Ao somar vários números, procure pares que somem 10, 100, 1000, etc. Isso simplifica a adição.
Exemplo: Calcular 7 + 6 + 4 + 13
•Agrupe (6 + 4) = 10.
•Agrupe (13 + 7) = 20.
•Some os resultados: 20 + 10 = 30.
5. Adição da Esquerda para a Direita
Ao invés de começar pela direita (unidades), comece pela esquerda (maior valor posicional). Isso pode ser melhor interpretado pelo cérebro e pode ser mais rápido em algumas situações.
Exemplo: Calcular 253 + 323
•Some as centenas: 200 + 300 = 500.
•Some as dezenas: 50 + 20 = 70.
•Some as unidades: 3 + 3 = 6.
•Combine os resultados: 500 + 70 + 6 = 576.
Estratégias para Subtração:
1. Decomposição de Números
Similar à adição, a decomposição pode ser usada para subtrair, quebrando o subtraendo em partes.
Exemplo: Calcular 78 – 23
•Decomponha 23 em 20 + 3.
•Subtraia 78 – 20 = 58.
•Subtraia o restante: 58 – 3 = 55.
2. Arredondamento e Compensação
transforme os números para a dezena, centena ou milhar mais próxima, faça a operação e depois faça as ponderações.
Exemplo: Calcular 62 – 19
•Arredonde 19 para 20 (adicionou 1).
•Subtraia 62 – 20 = 42.
•Compense adicionando o 1 que foi adicionado: 42 + 1 = 43.
3. Contagem Regressiva ou Progressiva
Para subtrações, pode-se contar para trás a partir do minuendo ou contar para frente do subtraendo até o minuendo para encontrar a diferença.
Exemplo (Contagem Regressiva): Calcular 25 – 6
•Comece com 25.
•Conte 6 unidades para baixo: 24, 23, 22, 21, 20, 19.
•Resultado: 19.
Exemplo (Contagem Progressiva): Calcular 25 – 19
•Comece em 19.
•Conte para frente até 25: 19 (para 20 é 1), 20 (para 25 é 5). Total: 1 + 5 = 6.
•Resultado: 6.
4. Subtração da Esquerda para a Direita
Assim como na adição, subtrair da esquerda para a direita pode ser mais fácil em algumas situações.
Exemplo: Calcular 538 – 224
•Subtraia as centenas: 500 – 200 = 300.
•Subtraia as dezenas: 50 – 10 = 40.
•Subtraia as unidades: 9 – 6 = 3.
•Combine os resultados: 300 + 40 + 3 = 343.
Praticar essas estratégias regularmente pode melhorar significativamente sua capacidade de realizar cálculos mentais, tornando-o mais eficiente em situações do dia a dia e em testes acadêmicos. A chave é a prática e a experimentação para descobrir quais estratégias funcionam melhor para você.
Adição e Subtração e Suas Relações com Outras Operações Matemáticas
A matemática é um campo interconectado, e a adição e a subtração não existem isoladamente. Elas estão intrinsecamente ligadas a outras operações, formando a base para a compreensão de conceitos mais avançados. Compreender essas relações é crucial para uma visão holística da aritmética.
1. Adição e Subtração: Operações Inversas
A adição e a subtração são as operações inversas uma da outra. Isso significa que uma desfaz o que a outra faz. Se você adiciona um número, pode subtrair o mesmo número para retornar ao valor original, e vice-versa.
Exemplo:
•Se 5 + 3 = 8, então 8 – 3 = 5 e 8 – 5 = 3.
•Se 10 – 4 = 6, então 6 + 4 = 10.
Essa relação é fundamental para a verificação de cálculos e para a resolução de equações simples. Se você sabe que a + b = c, então você também sabe que c – b = a e c – a = b. Essa compreensão da inversão é a base para a álgebra e para a resolução de problemas onde uma das parcelas ou o subtraendo/minuendo é desconhecido.
2. Adição e Multiplicação: Adição Repetida
A multiplicação pode ser vista como uma forma abreviada de adição repetida. Quando você multiplica dois números, está essencialmente adicionando um número a si mesmo um determinado número de vezes.
Exemplo:
•4 x 3 significa 4 adicionado a si mesmo 3 vezes: 4 + 4 + 4 = 12.
•Ou, 3 adicionado a si mesmo 4 vezes: 3 + 3 + 3 + 3 = 12.
Essa conexão é vital para entender o conceito de multiplicação e para realizar cálculos de forma mais eficiente. Por exemplo, se você precisa somar 5 + 5 + 5 + 5 + 5 + 5, é muito mais rápido calcular 5 x 6 = 30.
3. Subtração e Divisão: Subtração Repetida
A divisão, por sua vez, pode ser vista como uma forma abreviada de subtração repetida. Quando você divide um número por outro, está essencialmente subtraindo o divisor do dividendo repetidamente até que o resultado seja zero ou menor que o divisor.
Exemplo: Se você tem 12 maçãs e quer dividi-las igualmente em grupos de 3, você está essencialmente perguntando quantas vezes 3 pode ser subtraído de 12 até chegar a zero (12 – 3 = 9, 9 – 3 = 6, 6 – 3 = 3, 3 – 3 = 0 – 4 vezes). Isso significa que 12 dividido por 3 é 4.
4. Adição, Subtração e Potenciação/Radiciação
A potenciação é a multiplicação repetida de um número por si mesmo, e a radiciação é sua operação inversa. Embora não sejam diretamente operações de adição ou subtração, a compreensão de que a multiplicação é adição repetida e a divisão é subtração repetida nos permite ver a potenciação e a radiciação como operações que, em sua essência, envolvem a repetição de somas ou subtrações de forma mais complexa.
Ao visualizar essas interconexões, os alunos podem construir uma compreensão mais robusta da matemática como um todo, percebendo que as operações não são isoladas, mas sim partes de um sistema lógico e coerente. Essa perspectiva facilita a transição para conceitos mais avançados em álgebra, geometria e cálculo.
Aplicações Práticas da Adição e Subtração no Dia a Dia: Resolvendo Problemas Reais
A adição e a subtração são ferramentas indispensáveis para resolver uma vasta gama de problemas práticos em nosso cotidiano. Desde as tarefas mais simples até as decisões financeiras mais complexas, a capacidade de somar e subtrair com precisão é fundamental. Vamos explorar algumas das aplicações mais comuns e como essas operações nos ajudam a navegar pelo mundo.
1. Gestão Financeira Pessoal
Uma das aplicações mais evidentes da adição e subtração é na gestão do dinheiro. Seja para controlar gastos, somar receitas, calcular o troco ou planejar um orçamento, essas operações são a espinha dorsal das finanças pessoais.
Exemplo (Adição): Você recebe seu salário de R2.500,00etemumarendaextradeR 2.500,00 e tem uma renda extra de R2.500,00etemumarendaextradeR 300,00. Para saber sua renda total, você soma: R2.500,00+R 2.500,00 + R2.500,00+R 300,00 = R$ 2.800,00.
Exemplo (Subtração): Você tem R50,00egastaR 50,00 e gasta R50,00egastaR 18,00 em um lanche. Para saber quanto dinheiro sobrou, você subtrai: R50,00−R 50,00 – R50,00−R 18,00 = R$ 32,00.
2. Planejamento de Tempo e Eventos
A organização do tempo e planejamento de eventos são exemplos que precisam do conhecimento de adição e subtração. Seja para calcular a duração total de uma viagem, o tempo restante para um prazo ou a idade combinada de um grupo de pessoas, essas operações são cruciais.
Exemplo (Adição): Você precisa estudar para três provas. A primeira levará 2 horas, a segunda 3 horas e a terceira 1 hora e 30 minutos. Para saber o tempo total de estudo, você soma: 2 horas + 3 horas + 1 hora e 30 minutos = 6 horas e 30 minutos.
Exemplo (Subtração): Um evento está programado para começar às 19h e terminar às 22h. Para saber a duração do evento, você subtrai: 22h – 19h = 3 horas.
3. Culinária e Receitas
Na cozinha, a adição e a subtração são usadas para ajustar quantidades de ingredientes, especialmente quando se dobra ou reduz uma receita. Também é útil para calcular o tempo total de preparo e cozimento.
Exemplo (Adição): Uma receita pede 2 xícaras de farinha e 1 xícara de açúcar. Se você quiser fazer o dobro da receita, precisará de 2 + 2 = 4 xícaras de farinha e 1 + 1 = 2 xícaras de açúcar.
Exemplo (Subtração): Você tem 500g de chocolate e a receita pede 350g. Para saber quanto chocolate sobrará, você subtrai: 500g – 350g = 150g.
4. Esportes e Jogos
Em esportes e jogos, a adição e a subtração são constantemente utilizadas para manter a pontuação, calcular totais de pontos, ou determinar a diferença de pontos entre equipes.
Exemplo (Adição): Em um jogo de basquete, um jogador marcou 15 pontos no primeiro quarto, 10 no segundo, 8 no terceiro e 12 no último. Para saber o total de pontos do jogador, você soma: 15 + 10 + 8 + 12 = 45 pontos.
5. Construção e Engenharia
Profissionais da construção e engenharia utilizam a adição e a subtração para calcular dimensões, quantidades de materiais, custos e muito mais. Desde a soma de comprimentos de tubos até o cálculo de volumes de concreto, e a determinação de quanto material falta ou sobra, a precisão nessas operações é vital.
Exemplo (Subtração): Uma parede tem 4.5 metros de comprimento e você já pintou 2.1 metros. Para saber quanto falta pintar, você subtrai: 4.5 – 2.1 = 2.4 metros.
6. Estatística e Análise de Dados
No estudo das estatística, as operações estudas são primordiais para entender as somas, médias e outras medidas importantes. A subtração é usada para calcular desvios, variações e diferenças entre conjuntos de dados. Ao coletar dados, a primeira etapa geralmente envolve somar os valores para obter um total, que será usado em análises posteriores, e a subtração para comparar esses dados.
Exemplo (Subtração): Se a temperatura máxima em um dia foi de 30°C e a mínima foi de 18°C, a variação de temperatura foi de: 30°C – 18°C = 12°C.
Com isso, vemos que a adição e a subtração são habilidades que são fundamentais no nosso dia a dia. Dominar a adição e a subtração é, portanto, um passo fundamental para a autonomia e o sucesso em diversas áreas da vida.
A História da Adição e Subtração: Uma Jornada Através do Tempo
A adição e a subtração são operações milenares. Desde os primórdios da civilização, a necessidade de quantificar, combinar e remover objetos, animais ou pessoas impulsionou o desenvolvimento de métodos para somar e subtrair. A história dessas operações é, em muitos aspectos, a história do desenvolvimento do pensamento matemático e da civilização.
Contagem Primitiva e Marcas
Nos tempos pré-históricos, a adição e a subtração eram realizadas de maneiras muito simples, muitas vezes através de contagem um a um. Pastores contavam seus rebanhos usando pedras, marcas em ossos ou gravetos. Cada marca representava uma unidade, e a combinação de marcas em diferentes grupos era uma forma visual e tátil de adição. A remoção de marcas representava a subtração. O osso de Ishango, datado de cerca de 20.000 a.C., é um exemplo notável de um artefato que pode ter sido usado para contagem e, por extensão, para operações aditivas e subtrativas rudimentares.
Sistemas Numéricos Antigos
Com o surgimento das primeiras civilizações, sistemas numéricos mais sofisticados começaram a aparecer. Como, por exemplo, os egípcios que usavam um sistema de hieroglífico para contar e representar números muito grandes. A adição e a subtração eram realizadas agrupando ou desagrupando símbolos semelhantes e trocando dez símbolos de um tipo por um do próximo valor superior (similar ao nosso sistema decimal). O Papiro de Rhind, um antigo texto matemático egípcio, contém vários problemas que envolvem tanto a adição quanto a subtração.
Porém, os babilônios, desenvolveram um sistema sexagesimal, ou seja, tem como base 60. A adição e a subtração eram realizadas de forma posicional, mas com a complexidade de ter 60 símbolos para cada posição. Apesar disso, eles eram capazes de realizar cálculos aditivos e subtrativos complexos para fins astronômicos e comerciais.
A Contribuição Grega e Romana
Os gregos, embora brilhantes em geometria, não desenvolveram um sistema numérico posicional que facilitasse a aritmética. Eles usavam letras do alfabeto para representar números, o que tornava a adição e a subtração processos mais laboriosos, muitas vezes dependendo de ábacos ou cálculos mentais. Os romanos, com seu sistema de numeração baseado em letras (I, V, X, L, C, D, M), também enfrentavam desafios nessas operações, que eram frequentemente realizadas com o auxílio de ábacos.
O Ábaco: Uma Ferramenta Revolucionária
O ábaco, em suas diversas formas (sumério, chinês, romano, japonês), foi uma das ferramentas mais importantes na história da adição e subtração. Ele permitia que as pessoas realizassem somas e subtrações complexas de forma rápida e eficiente, manipulando contas que representavam valores posicionais. O ábaco foi, por muitos séculos, a principal “calculadora” do mundo, e sua influência pode ser vista até hoje em como pensamos sobre o valor posicional dos números.
A Inovação Indiana e Árabe: O Sistema Decimal Posicional
O maior avanço que se teve no campo das operações foi a introdução do do sistema de numeração indo-arábico, que é o sistema decimal posicional que usamos hoje. Este sistema foi pioneiro no conceito de valor posicional e também, o número zero como um marcador de lugar. Isso permitiu que qualquer número, por maior que fosse, fosse representado usando apenas dez dígitos (0-9).
Os matemáticos árabes, como Al-Khwarizmi (século IX), foram fundamentais na disseminação e aprimoramento desse sistema. Eles desenvolveram algoritmos para as operações aritméticas, incluindo a adição e a subtração, que eram muito mais eficientes do que os métodos anteriores.
A Chegada à Europa e a Era Moderna
O sistema indo-arábico e seus métodos de adição e subtração chegaram à Europa através do comércio e das traduções de textos árabes, notavelmente pelo trabalho de Leonardo Fibonacci (século XIII), que produziu o livro que divulgou para o mundo o sistema que usamos hoje. No entanto, a transição não foi imediata; o ábaco e os algarismos romanos coexistiram com os novos algarismos por séculos.
Com a invenção da tecnologia e a necessidade de cálculos rápidos e precisos para o comercio, por essas e outras ocasiões o sistema foi tornando-se mundialmente conhecido e usados. A partir do século XVII, as primeiras calculadoras apareceram, dando o primeiro passo para a criação de computadores mais modernos.
Hoje, a adição e a subtração são operações que realizamos sem pensar, seja mentalmente, com uma calculadora ou através de um computador. No entanto, sua longa e rica história nos lembra que essas operações fundamentais são o resultado de milênios de engenhosidade humana e da busca incessante por maneiras mais eficientes de entender e manipular o mundo quantitativo.
